线性模型是机器学习里面最基础的一个模型，也是比较简单的

• 线性模型主要用于属于线性关系的模型，像y=wx+b，就是只有一个属性x表示的y值的变化规律，也称做单属性线性回归。

基本形式

• 当给定d个属性示例$x={x_1;x_2....x_d}$，线性模型视图学得一个属性的线性组合来进行预测：$f(x)=w_1x_1+w_2x_2+w_3x_4+...w_dx_d+b=w^T+b$，w和b确认后，模型即可确认。
• 线性模型形式简单、易于建模，却蕴涵着机器学习中的一些重要的基本思想。许多功能更为强大的非线性模型（nonlinear model）可以在线性模型的基础上通过引入层级结构或者高维映射而得。

线性回归

度量指标

• 集中趋势的衡量

  • 均值：$\bar{x}=\frac{\sum{i=1}^nx_i}{n}$；
  • 中位数：大小排序后，中间位置的数；
  • 众数：出现最多的数；

• 离散程度的衡量

  • 方差:$s^2=\frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}$
  • 标准差：s

单属性线性回归

• 先研究单属性线性回归问题，也即：

  1. 训练集只有一个属性
  2. 给定数据集$D={(x_i,y_i)}m_i=1$
  3. 线性预测表示为：$f(x_i=wx_i+b)$
  4. 通过训练集得到w和b的值，使得$f(x_i)≈y_i$

• 均方差是常用的性能度量指标：

$(\omega^*,b^*)=\arg\min_{(\omega,b)}\sum_{i=1}^{m}{(f(x_i)-y_i)^2}=\arg\min_{(\omega,b)}\sum_{i=1}^{m}{(y_i-\omega x_i-b)^2}$

• 只需针对w和b分别求偏导即可得到最优解（闭式close-form解）w和b。
• 基于均方误差最小化来进行模型求解的方法也称为最小二乘法。在线性回归中，最小二乘法可以找到一条这样的直线，使得所有样本到直线上的欧氏距离之和最小。

$w=\frac{\sum (x_i-\overline x)(y_i-\overline y)}{\sum (x_i-\overline x)^2}$

$b=\overline y -w\overline x$

多属性线性回归

• 多元线性回归也就是有d个属性，建立矩阵方程。

线性回归与最小二乘

$y=w^Tx+ε$

• 假设ε满足独立同分布，服从均值0方差$θ^2$的高斯分布。所以ε表示为：$p(ε)=\frac{1}{\sqrt{2π}}e^{(-\frac{ε^2}{2σ^2})}$
• 由于$ε=y-w^Tx$，带入到上式：$p(y|x;w)=\frac{1}{\sqrt{2π}}e^{(-\frac{(y-w^Tx)^2}{2σ^2})}$
• 其中$p(y|x;w)$表示w能够最大y的概率的取值，可以用似然函数求解。

$L(θ)=\prod_{i=1}{m}p(y|x;w)$

• 通过取对数，化简得到目标函数：求取J(θ)的最小值

$J(θ)=\frac{1}{2}\sum_{i=1}^m (h_θ(x)-y)^2$

• 最小值可以通过凸函数的导数为零的解，由于X和θ是矩阵，求导要符合矩阵求导的公式。求导公式，可参照wiki百科

$J(\theta)=\frac{1}{2}\sum_{i=1}{m}{(h_\theta(x^{(i)})-y^{(i)})}=\frac{1}{2}(X\theta-y)^T(X\theta-y)$

$\nabla_\theta J(\theta)=\nabla_\theta (\frac{1}{2}(X\theta-y)^T(X\theta-y))$

$=\nabla_\theta(\frac{1}{2}(X^T\theta^T-y^T)(X\theta-y))$

$=\nabla_\theta(\frac{1}{2}(\theta^TX^TX\theta-\theta^TX^Ty+y^TX\theta-y^Ty))$

$=\frac{1}{2}(2X^TX\theta-X^Ty+(y^TX)^T)=X^TX\theta-X^Ty$

$\theta=(X^TX)^{-1}X^Ty$

岭回归

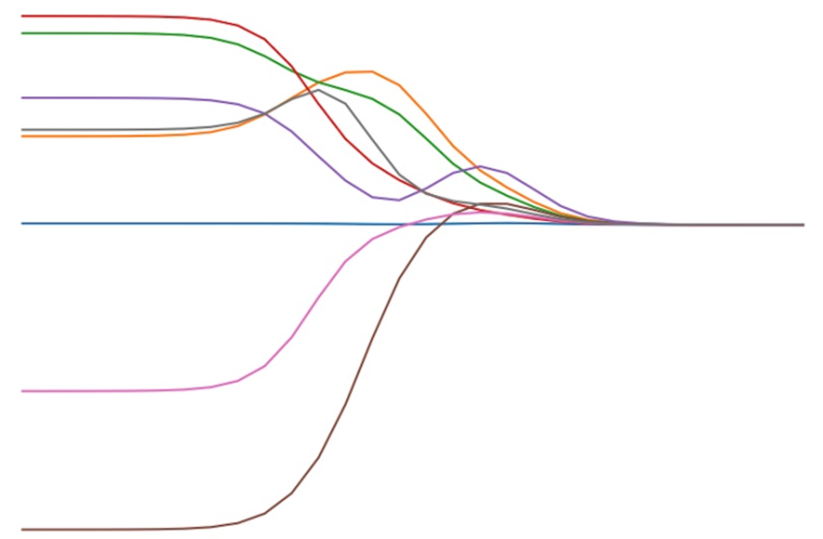
• 岭回归和Lasso是两种线性回归的缩减(shrinkage)方法。
• 标准最小二乘法优化问题:

$J(θ)=\frac{1}{2}\sum_{i=1}^m (h_θ(x)-y)^2$

• 可以表示为：

$J(θ)=\frac{1}{2} (h_θ(x)-y)^T(h_θ(x)-y)$

• 回归系数为：

$θ=(X^TX)^{-1}X^Ty$

• 这个问题解存在且唯一的条件就是XX列满秩: rank(X) = dim(X)。但即使 X 列满秩，但是当数据特征中存在共线性，即相关性比较大的时候，会使得标准最小二乘求解不稳定, $X^TX$的行列式接近零，计算$X^TX$的时候误差会很大。这个时候我们需要在cost function上添加一个惩罚项 $\lambda\sum_{i=1}^{n}θ_{i}^2$，称为L2正则化。
• 这个时候的cost function的形式就为:

$f(θ) = \sum_{i=1}^{m} (y_i - x_{i}^{T}θ)^2 + \lambda\sum_{i=1}^{n}θ_{i}^{2}$

• 通过加入此惩罚项进行优化后，限制了回归系数$w_i$的绝对值，数学上可以证明上式的等价形式如下:

$f(θ) = \sum_{i=1}^{m} (y_i - x_{i}^{T}θ)^2$

$s.t. \sum_{i=1}^{n}θ_{j}^2 \le t$

• 其中t为某个阈值。

• 将岭回归系数用矩阵的形式表示:

$\hat{θ} = (X^{T}X + \lambda I)^{-1}X^{T}y$

• 可以看到，就是通过将 $X^TX$ 加上一个单位矩阵是的矩阵变成非奇异矩阵并可以进行求逆运算。

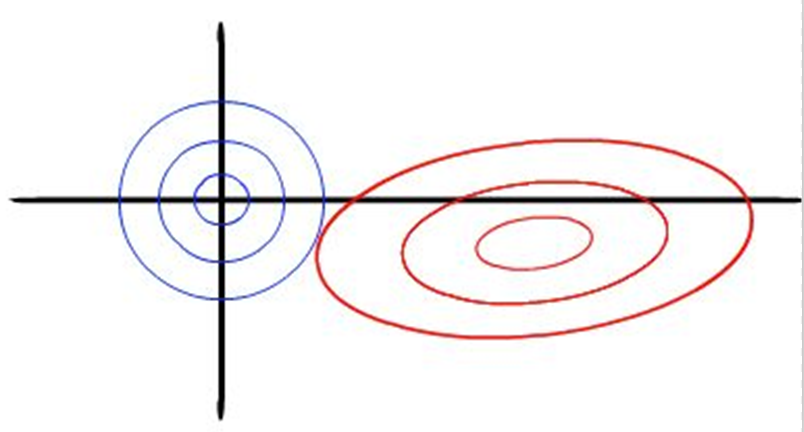
岭回归的一些性质

• 当岭参数 $\lambda = 0$时，得到的解是最小二乘解
• 当岭参数 $\lambda$ 趋向更大时，岭回归系数 $θ_i$趋向于0，约束项 t 很小

Lasso

• 岭回归限定了所有回归系数的平方和不大于 t , 在使用普通最小二乘法回归的时候当两个变量具有相关性的时候，可能会使得其中一个系数是个很大正数，另一个系数是很大的负数。通过岭回归的 $\sum_{i=1}^{n} θ_i \le t$的限制，可以避免这个问题。

• LASSO(The Least Absolute Shrinkage and Selection Operator)是另一种缩减方法，将回归系数收缩在一定的区域内。LASSO的主要思想是构造一个一阶惩罚函数获得一个精炼的模型, 通过最终确定一些变量的系数为0进行特征筛选。

• LASSO的惩罚项为:

$\sum_{i=1}^{n} \vert θ_i \vert \le t$

• 与岭回归的不同在于，此约束条件使用了绝对值的一阶惩罚函数代替了平方和的二阶函数。虽然只是形式稍有不同，但是得到的结果却又很大差别。在LASSO中，当λ很小的时候，一些系数会随着变为0而岭回归却很难使得某个系数恰好缩减为0. 我们可以通过几何解释看到LASSO与岭回归之间的不同。

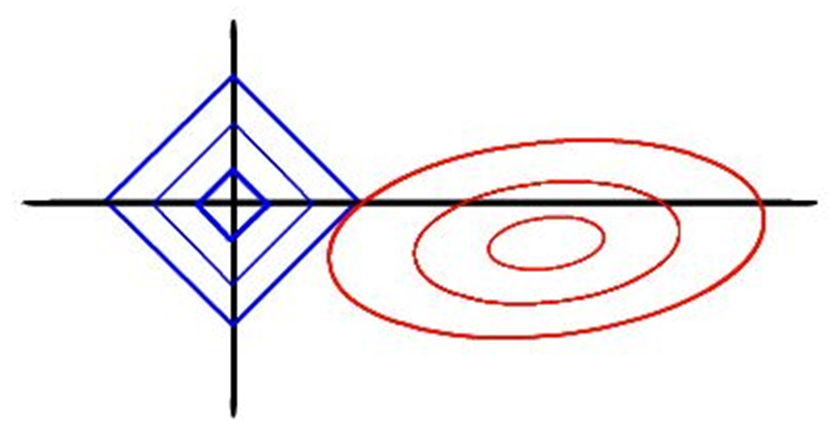
• 虽然惩罚函数只是做了细微的变化，但是相比岭回归可以直接通过矩阵运算得到回归系数相比，LASSO的计算变得相对复杂。

Kernel Regression and RBFs

• 径向基函数
• 我们可以用核函数线性组合来表示线性回归模型：

$Φ(x)=[κ(x,μ_1,λ),...,κ(x,μ_d,λ)]$，e.g. 高斯核函数：$κ(x,μ,λ)=e^{-\frac{1}{2}||x-μ_i||^2}$

• d的确定可以指定，这个可以使用x的个数，但是如果x个数太多，那么会导致很复杂。第二个方法可以通过Kmeans聚类。
• 超参数的确定，λ取0.1，μ取在x聚类后的均值。（还没验证…）

分类

广义线性回归

• 线性回归模型$y=w^Tx+b$，如果将y表示为在指数尺度上的变化，则：$\ln y=w^Tx+b$称为对数线性回归。$y=e^{w^Tx+b}$，实质上是在求输入空间到输出空间的非线性函数的映射（欧拉公式）。
  
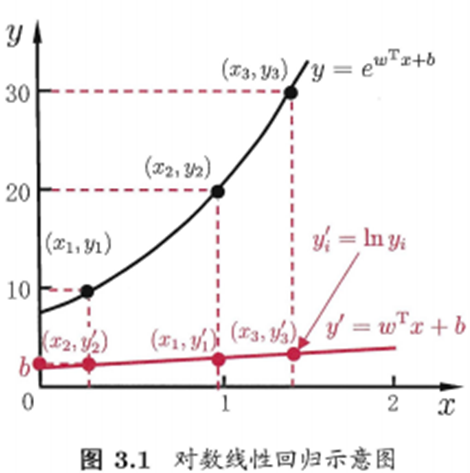
• 对更一般的单调可微函数g(x)，$y=g^{-1}(w^Tx+b)$这样的模型成为广义线性模型。g(x)称为联系函数（link function）

对数几率函数（逻辑回归）

• 之前讨论的是使用线性模型进行回归学习，如果要应用到分类中，思路就是利用广义线性模型，找一单调可微函数将分类任务的真实标记y与线性回归模型的预测值对应起来即可。

• 设$z=w^Tx+b$，单位阶跃函数（unit-step function）表示为：
  $y=\begin{cases}0,z<0;\\0.5,z=0;\\1z>0\end{cases}$

• 可以表征二分类任务，z大于零为正例，小于零为负例，临界值可任意。但是单位阶跃不连续，固需利用类似的替代函数（surrogate function）：对数几率函数（logistic function）$y=\frac{1}{1+\exp{-z}}$

• 目前使用比较广泛的是对数几率函数logistic function，它是Sigmoid函数的一种。它的好处在于：

  1. 单调可微
  2. 在0处变化陡峭，最接近阶跃函数，适合二分类。

• $y=\frac{1}{1+\exp{-(w^Tx+b)}}$，$\ln \frac{y}{1-y}=w^Tx+b$，$\frac{y}{1-y}$含义就是比率，为正例的可能性与为反例的可能性比值。

• 从本质上讲，对数几率回归模型logistic regression就是在用线性回归模型的预测结果去逼近真实标记的对数几率。

• 确定模型之后，接下来自然要做的就是确定w和b。这里要使用到的方法是极大似然法（maximum likelihood method）。

• 给定数据集{$(x_i,y_i)$}i=1~m，对率回归模型最大化就是要把所有样本概率预测之和最大化，也就是$l(w,b)=\sum{i=1}^m \ln p(y_i|x_i;w,b)$。为方便讨论，令β=(w;b),x̂ =(x;1),wT+x=βTx̂ ，再令$l(β)=\sum{i=1}^m -y_iβ^Tx_i\ln (1+\exp{β^Tx_i})$这样，最大化原概率和公式等价于最小化。上式为关于β的高阶可导连续凸函数，根据凸优化理论，利用经典的数值优化算法如梯度下降法、牛顿法都可求得最优解。

logistic回归求解

• 回归的方程表达式为：

$h_θ(x)=g(θ^Tx)=\frac{1}{1+e^(-θ^Tx)}$

$h_θ(x)$可以进行概率表示：

$P(y=1|x;θ)=h_θ(x)$

$P(y=0|x;θ)=1-h_θ(x)$

• 结合到一起可以写为：

$P(y|x;θ)=(h_θ(x))^y(1-h_θ(x))^{1-y}$

• 是不是很巧妙。
• 然后找到最大似然估计：

$log L(θ)=\sum_{i=1}^my\log h(x)+(1-y)\log(1-h(x))$

$J(θ)=-\frac{1}{2m}log L(θ)$

• 由于是非线性方程找不到驻点，所以只能用梯度下降法，求导方向下降最大的点移动。

$h_\theta(x)=\theta_1x+\theta_0$

$J(\theta_0,\theta_1)=\frac{1}{2m}\sum^{m}_{i=1}(h_\theta{(x_i)}-y_i)^2$

$\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_0}=\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x_i)-y_i)$

$\frac{\partial J(\theta_1)}{\partial\theta_0}=\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x_i)-y_i)\times x_i$

$\theta_1:=\theta_1-\alpha\times\frac{\partial J(\theta_0,\theta_1)}{\theta_0} \; \theta_0:=\theta_0-\alpha\times\frac{\partial J(\theta_0,\theta_1)}{\theta_1}$

线性判别分析

• 线性判别分析Linear Discriminant Analysis是一种经典的线性学习方法，应用于分类任务中。
• LDA的思想非常简单，将训练集的样本投影到一条直线上，同一类的尽量互相靠近，而不同类之间尽可能相隔的远。使用数学语言，投影即是向量乘积， 同一类尽量靠近，就是协方差要小，不同类相隔远，就是类中心距离远，也就是均值投影的差要大。

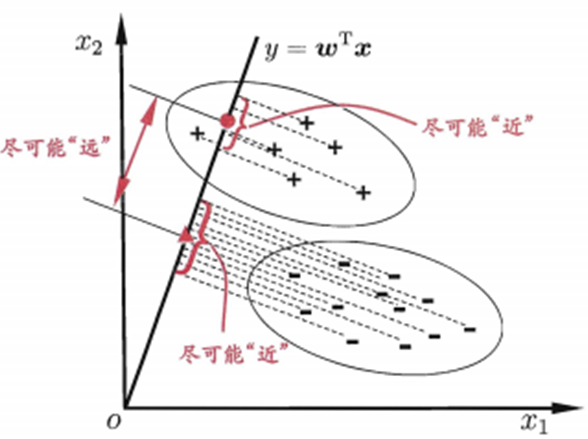
1. 从贝叶斯决策理论的角度可以证明LDA在两类数据同先验、满足高斯分布且协方差相等时，LDA可达到最优分类。
2. LDA核心是投影，这样往往实现了降维，因而LDA也常被视为一种经典的监督降维技术。

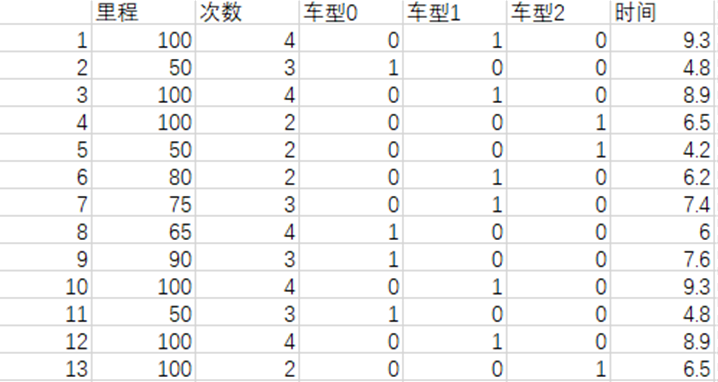
import numpy as np
from sklearn import linear_model
train_data=pd.read_csv('./data/linear3.csv',index_col=0)
x=train_data.iloc[:,0:5]
y=train_data.iloc[:,5]
clf = linear_model.LinearRegression()
clf.fit(x,y)
print(clf.coef_) # 斜率
print(clf.intercept_) # 截距

# 最小二乘法
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
class LinearRegression:
    def __init__(self):
        self.w=None
    def fit(self,x,y):
        x=np.insert(x,0,1,axis=1)
        x_=np.linalg.inv(x.T.dot(x))
        self.w=x_.dot(x.T).dot(y)
    def predict(self,x):
        x=np.insert(x,0,1,axis=1) # 插入了b
        y_pred=x.dot(self.w)
        return y_pred
def mean_squared_error(y_true,y_pred):
    mse=np.mean(np.power(y_true-y_pred,2))
    return mse
diabetes=datasets.load_diabetes()
x=diabetes.data[:,np.newaxis,2]
print(x.shape)
x_train,x_test=x[:-20],x[-20:]
y_train,y_test=diabetes.target[:-20],diabetes.target[-20:]
clf=LinearRegression()
clf.fit(x_train,y_train)
y_pred=clf.predict(x_test)
print('MSE',mean_squared_error(y_test,y_pred))
plt.scatter(x_test[:,0],y_test,color='black')
plt.plot(x_test[:,0],y_pred,color='blue',linewidth=3)
plt.show()

import random
import numpy as np
def gradientDescent(x,y,theta,alpha,m,numIterations):
    xTrans=x.transpose()
    for i in range(0,numIterations):
        hypothesis=np.dot(x,theta)
        loss=hypothesis-y
        cost=np.sum(loss**2)/(2*m)
        gradient=np.dot(xTrans,loss)/m
        theta=theta-alpha*gradient
    return theta
def genData(numPoints,bias,variance):
    x=np.zeros(shape=(numPoints,2))
    y=np.zeros(shape=numPoints)
    for i in range(0,numPoints):
        x[i][0]=1
        x[i][1]=i
        y[i]=(i+bias)+random.uniform(0,1)*variance
    return x,y
x,y=genData(100,25,10)
# print(x,y)
m,n=np.shape(x)  # m代表多少个实例
numIterations=100000  # 循环次数
alpha=0.0005  #学习率
theta=np.ones(n)  # 要求得的参数值
theta=gradientDescent(x,y,theta,alpha,m,numIterations)
print(theta)

回归中的相关度和R平方值

• 相关度

$\rho = Cor(X,Y)=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}$

• 相关系数：-1负相关，0不相关，1正相关。
• R平方值

$r_{xy}=\frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^2(y-\bar{y})^2} }$

• 决定系数，反应因变量的全部变异能通过回归关系被自变量解释的比例。
  • 简单线性回归：$R^2=r^2$相关度
  • 多远线性回归：

$r^2=\frac{SSR}{SSt}=\frac{\sum{(\widehat y_i-\bar y)^2}}{(y_i- \bar{y})^2}$

$SS_T=\sum_{i}(y_i-\bar{y})^2,SS_R=\sum_{i}(\hat{y}_i-\bar{y})^2,SS_E=\sum_{i}(y_i-\bar{y}_i)^2$

• R随着自变量数量增加而增大，R平方跟样本量是有关系的。因此做了以下修正：

$R^2_{adjusted}=1-\frac{(1-R^2)(N-1)}{N-p-1}$

where:
R^2 = sample R-square
p=Number of predictors
N=Total sample size