神经网络算法
联结主义:神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
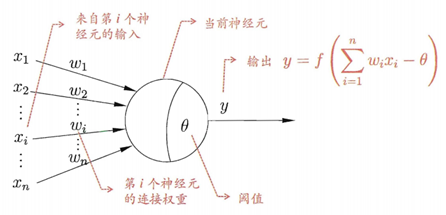
神经网络中最基本的成分是神经元(neuron)模型,即“简单单元”,在生物神经网络中,每个神经元与其他神经元相连,当它“兴奋”时,就会向相连的神经元发送化学物质,从而改变这些神经元内的电位;如果某神经元的电位超过一个“阈值(threshold)”,那么它就会被激活,即“兴奋” 起来,向其他神经元发送化学物质。
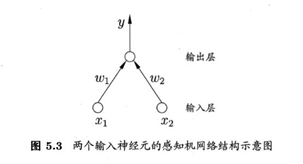
感知机由单个神经元组成的单层神经网络,树突接收其他轴突传递来的信息,在通过自己的轴突传递出去。感知机三个功能:加权、求和、激励
权重及阈值θ通过学习获得,阈值θ可看做一个固定输入为-1的哑结点(dummy node)所对应的权重 。这样权重和阈值可以统一学习。对训练样例(x,y),感知机输出 ,学习规则:w i ← w i + ∇ w i w_i←w_i+\nabla{w_i} w i ← w i + ∇ w i ∇ w i = η ( y − y ^ ) x i \nabla{w_i}=η(y-\widehat{y})x_i ∇ w i = η ( y − y ) x i
η∈(0,1)称为学习率(learning rate)。
每一轮迭代中我们都要判断某个输入实例是不是误判点,即y i ( w x i + b ) < = 0 y_i(wx_i+b)<=0 y i ( w x i + b ) < = 0
使用对偶形式,判断条件改为:y i ( ∑ j = 1 N a j y j x j x i + b ) y_i(\sum_{j=1}^{N}a_jy_jx_jx_i+b) y i ( ∑ j = 1 N a j y j x j x i + b ) G = [ x i x j ] N ∗ N G=[x_ix_j]_{N*N} G = [ x i x j ] N ∗ N
对偶形式的目的是降低运算量,但是并不是在任何情况下都能降低运算量,而是在特征空间的维度很高时才起到作用。
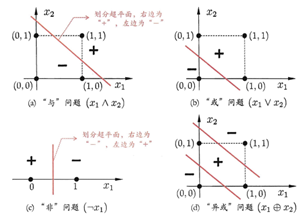
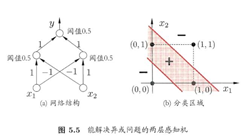
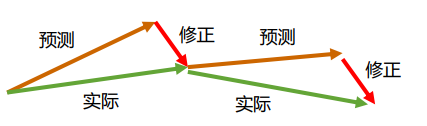
感知机只有输出层神经元进行激活函数处理,即只拥有一层功能神经元。与或非问题都是线性可分(linearly separable)。感知机对线性可分学习过程一定收敛,非线性可分问题w难以稳定下来,不能求合适的解,如下图。
输入层:x i ( i = 0 , . . . d ) x_i(i=0,...d) x i ( i = 0 , . . . d )
隐藏层:隐藏单元z h ( h = 1 , . . . H ) z_h(h=1,...H) z h ( h = 1 , . . . H )
输出层:y i ( i = 0 , . . . K ) y_i(i=0,...K) y i ( i = 0 , . . . K )
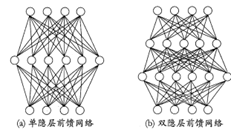
多层感知机层与层之间是全连接的
网络结构中,输入层与输出层之间的神经元层成为隐含层(hidden layer),每层神经元与下一层神经元完全互联,神经元之间不存在同层连接,也不存在跨层连接,称为多层前馈网络结构 (multi-layer feedforward nerual networks)
多层网络:包含隐层的网络
前馈网络:神经元之间不存在同层连接也不存在跨层连接
隐层和输出层具有激活函数,所以这两层的神经元亦称“功能单元”。多层前馈网络有强大的表示能力。只需一个包含足够多神经元的隐层,多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数。设置隐层神经元数,通常用“试错法”。
主要特点:信号是前向传播的,而误差是反向传播的。
主要过程:信号的前向传播,从输入层经过隐含层,最后到达输出层
误差的反向传播,从输出层到隐含层,最后到输入层,依次调节隐含层到输出层的权重和偏置,输入层到隐含层的权重和偏置
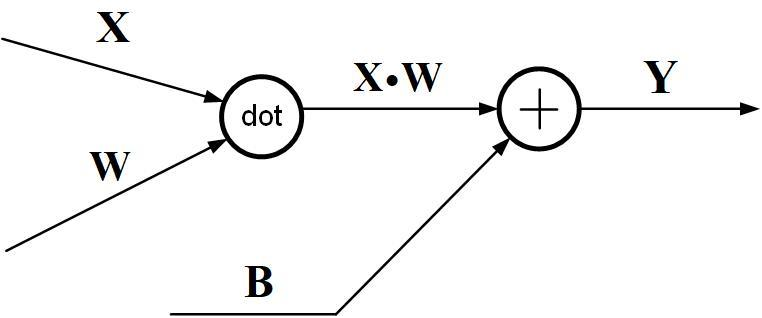
放射变换:Y = X ⋅ W + B Y=X \cdot W +B Y = X ⋅ W + B
X = ( x 0 , . . . x n ) X=(x_0,...x_n) X = ( x 0 , . . . x n )
J是代价函数
∂ J ∂ X = ( ∂ J ∂ x 0 . . . ) \frac{\partial J}{\partial X}=(\frac{\partial J}{\partial x_0}...) ∂ X ∂ J = ( ∂ x 0 ∂ J . . . ) ∂ J ∂ X = ∂ J ∂ Y ⋅ W T \frac{\partial J}{\partial X}=\frac{\partial J}{\partial Y}\cdot W^T ∂ X ∂ J = ∂ Y ∂ J ⋅ W T ∂ J ∂ W = X T ⋅ ∂ J ∂ Y \frac{\partial J}{\partial W}=X^T\cdot\frac{\partial J}{\partial Y} ∂ W ∂ J = X T ⋅ ∂ Y ∂ J
隐层一般使用sigmoid、tanh、relu
输出层根据任务不同,二分类问题使用sigmoid、tanh、relu,多分类使用softmax
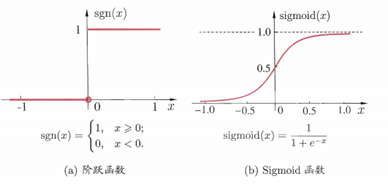
理想激活函数是阶跃函数,0 表示抑制神经元,而1表示激活神经元
阶跃函数具有不连续、不光滑等不好的性质,常用的是Sigmoid函数
s t e p f u n c ( x ) = 1 i f x > 0 e l s e 0 stepfunc(x)=1\;if\;x>0\;else\;0
s t e p f u n c ( x ) = 1 i f x > 0 e l s e 0
Sigmoid函数可能在较大范围内变化的输入值挤压到(0,1)输出值范围内,因此有时也称为”挤压函数”
把这样许多个神经元按一定的层次结构连接起来,就得到了神经网络。
s i g m o i d ( x ) = 1 1 + e − x sigmoid(x)=\frac{1}{1+e^{-x}}
s i g m o i d ( x ) = 1 + e − x 1
f ( x ) = t a n h ( x ) = e x − e − x e x + e − x f(x)=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
f ( x ) = t a n h ( x ) = e x + e − x e x − e − x
x = np.linspace(-10 ,10 ) y = np.tanh(x)
r e l u ( x ) = m a x { 0 , x } relu(x)=max\{0,x\}
r e l u ( x ) = m a x { 0 , x }
r e l u ( x ) = m a x { 0.1 x , x } relu(x)=max\{0.1x,x\}
r e l u ( x ) = m a x { 0 . 1 x , x }
{ x if x > 0 α ( e x − 1 ) if x ≤ 0 \begin{cases}
x & \text{ if } x>0 \\ \alpha (e^x-1) & \text{ if } x\le0\end{cases} { x α ( e x − 1 ) if x > 0 if x ≤ 0
r e l u ( x ) = m i n ( m a x { 0 , x } , 6 ) relu(x)=min(max\{0,x\},6)
r e l u ( x ) = m i n ( m a x { 0 , x } , 6 )
使用sigmoid函数:σ ( ω T x + b ) = 1 1 + e − ( ω T x + b ) \sigma(\omega^Tx+b)=\frac{1}{1+e^{-(\omega^Tx+b)}} σ ( ω T x + b ) = 1 + e − ( ω T x + b ) 1
条件概率为:p w ( y = 1 ∣ x ) = σ ( ω T x + b ) p_w(y=1|x)=\sigma(\omega^Tx+b) p w ( y = 1 ∣ x ) = σ ( ω T x + b ) p w ( y = 0 ∣ x ) = 1 − σ ( ω T x + b ) p_w(y=0|x)=1-\sigma(\omega^Tx+b) p w ( y = 0 ∣ x ) = 1 − σ ( ω T x + b )
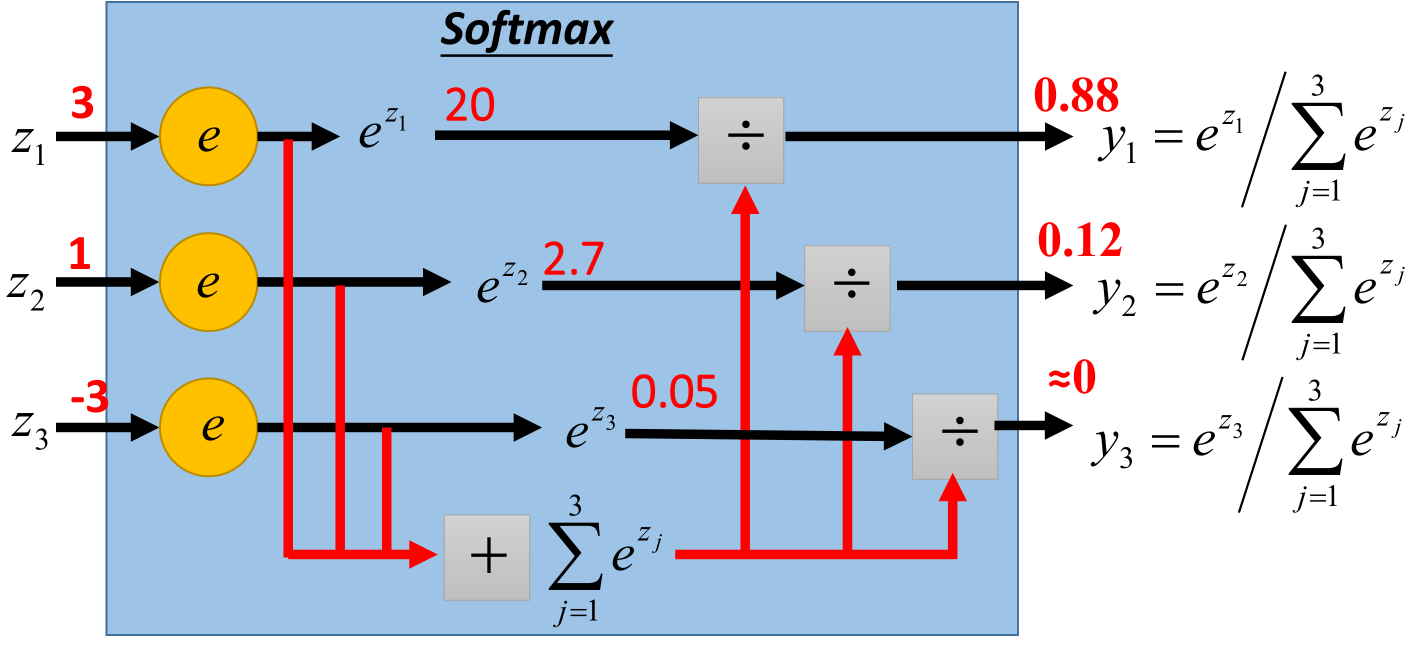
假设有一个数组V,V i V_i V i
S i = e i ∑ j e j S_i=\frac{e^i}{\sum_j{e^j}} S i = ∑ j e j e i 把大范围的输入转为[0,1]范围的概率形式
def softmax (x ): if x.ndim == 2 : x = x.T x = x - np.max(x, axis=0 ) y = np.exp(x) / np.sum(np.exp(x), axis=0 ) return y.T x = x - np.max(x) return np.exp(x) / np.sum(np.exp(x))
又称目标函数(objective function),或误差函数(error function),或代价函数(cost function) , 或经验风险(empirical risk);用来度量网络实际输出与期望输出之间的不一致程度,指导网络的参数学习和表示学习。
SSE(Sum of Squared Error)均方误差和
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}{(h_\theta(x^{(i)})-y^{(i)})^2}+\lambda\sum_{j=1}^{n}{\theta^2_j} J ( θ ) = 2 m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2
CE(Cross Entropy)交叉熵,对数损失
J ( θ ) = − 1 m ∑ i = 1 m y ( i ) ln h θ ( x ( i ) ) + ( 1 − y ( i ) ) ln ( 1 − h θ ( x ( i ) ) ) + λ ∑ j = 1 n θ j 2 J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}{y^{(i)}\ln{h_\theta(x^{(i)})+(1-y^{(i)})\ln{(1-h_\theta(x^{(i)})})}}+\lambda\sum^{n}_{j=1}{\theta^2_j} J ( θ ) = − m 1 ∑ i = 1 m y ( i ) ln h θ ( x ( i ) ) + ( 1 − y ( i ) ) ln ( 1 − h θ ( x ( i ) ) ) + λ ∑ j = 1 n θ j 2
熵 用于度量变量不确定性的程度:H ( X ) = − ∑ i = 1 n p ( x i ) log p ( x i ) H(X)=-\sum^{n}_{i=1}{p(x_i)\log{p(x_i)}} H ( X ) = − ∑ i = 1 n p ( x i ) log p ( x i )
交叉熵 用于度量两个概率分布间的差异性信息,越确信交叉熵越小
设 p(x),q(x) 分别是离散随机变量X的两个概率分布,其中p(x)是目标分布,p和q的交叉熵可以看做是,使用分布q(x) 表示目标分布p(x)的困难程度:H ( p , q ) = ∑ i p ( x i ) log 1 log q ( x i ) = − ∑ i p ( x i ) log q ( x i ) H(p,q)=\sum_i{p(x_i)\log{\frac{1}{\log{q(x_i)}}}}=-\sum_i{p(x_i)\log{q(x_i)}} H ( p , q ) = ∑ i p ( x i ) log log q ( x i ) 1 = − ∑ i p ( x i ) log q ( x i )
交叉熵损失 用于描述真实概率和模型预测概率的交叉熵
softmax得到预测的概率之后,把标签进行独热编码,再使用交叉熵损失函数优化模型。
若p ( y ) p(y) p ( y ) q ( y ) q(y) q ( y ) Kullback-Leibler Divergence。简称KL散度。度量两分布的差异:D K L ( P ∣ ∣ Q ) = − ∑ x ∈ X p ( x ) log q ( x ) + ∑ x ∈ X p ( x ) log p ( x ) = H ( P , Q ) − H ( P ) D_{KL}(P||Q)=-\sum_{x\in X}{p(x)\log{q(x)}}+\sum_{x\in X}{p(x)\log{p(x)}}=H(P,Q)-H(P) D K L ( P ∣ ∣ Q ) = − ∑ x ∈ X p ( x ) log q ( x ) + ∑ x ∈ X p ( x ) log p ( x ) = H ( P , Q ) − H ( P )
def cross_entropy_error (y, t ): delta = 1e-7 return -np.sum(t * np.log(y + delta))
由于交叉熵损失需要先将输出经过softmax,当输出结果较多时,计算量指数增加。
铰链损失函数(Hinge Loss)不需要输出的概率值,就可以得到输出损失
L o s s = ∑ j ≠ y i m a x ( 0 , f ( x i , W ) j − f ( x i , W ) y j + △ ) Loss=\sum_{j\ne y_i}^{}{max(0,f(x_i,W)_j-f(x_i,W)_{y_j}+\triangle)}
L o s s = j = y i ∑ m a x ( 0 , f ( x i , W ) j − f ( x i , W ) y j + △ )
求解非线性无约束优化问题的基本方法
w i + 1 = w i − a ∂ J ∂ x w_{i+1}=w_i-a\frac{\partial{J}}{\partial{x}} w i + 1 = w i − a ∂ x ∂ J J是损失函数,沿负梯度方向迭代求解最优参数,a是学习率
(Batch Gradient Descent )利用全部训练数据集计算损失函数的梯度来执行一次参数更新
θ ⇒ θ − η ⋅ ▽ J ( θ ) \theta\Rightarrow\theta-\eta\cdot\triangledown{J(\theta)} θ ⇒ θ − η ⋅ ▽ J ( θ )
缺点:更新较慢、不能在线更新模型
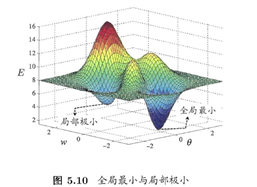
优点:对凹函数可得到全局最小,非凸函数可收敛到局部极小
SGD (Stochastic Gradient Descent)对每一个训练样本点和标签执行参数更新
θ ⇒ θ − η ⋅ ▽ J ( θ ; x ( i ) ; y ( i ) ) \theta\Rightarrow\theta-\eta\cdot\triangledown{J(\theta;x^{(i)};y^{(i)})} θ ⇒ θ − η ⋅ ▽ J ( θ ; x ( i ) ; y ( i ) ) 缺点:梯度精度差、目标函数下降过程出现较大波动、难以跳出局部极小值点和鞍点
优点:速度快,可在线学习
class SGD : def __init__ (self, lr=0.01 ): self.lr = lr def update (self, params, grads ): for key in params.keys(): params[key] -= self.lr * grads[key]
(Mini-batch Gradient Descent)每𝑚个训练样本点,进行一次参数更新
θ ⇒ θ − η ⋅ ▽ J ( θ ; x ( i : i + m ) ; y ( i : i + m ) ) \theta\Rightarrow\theta-\eta\cdot\triangledown{J(\theta;x^{(i:i+m)};y^{(i:i+m)})} θ ⇒ θ − η ⋅ ▽ J ( θ ; x ( i : i + m ) ; y ( i : i + m ) ) Batch-GD和单样本SGD方法的折衷
优点:减小了参数更新的方差,可平稳收敛;速度快,可利用优化的矩阵运算库来高效的计算梯度
Batch大小根据问题来定。一般而言设为32、 64、 128或256即可。
动量法,把过去时间步骤更新矢量的一部分(𝛾)加到当前更新矢量
v 1 = η ▽ J ( θ ) v1=\eta\triangledown{J(\theta)} v 1 = η ▽ J ( θ ) v k = γ v k − 1 + η ▽ J ( θ k − 1 ) , γ ∈ ( 0 , 1 ) v_k=\gamma v_{k-1}+\eta\triangledown J(\theta_{k-1}), \gamma\in(0,1) v k = γ v k − 1 + η ▽ J ( θ k − 1 ) , γ ∈ ( 0 , 1 ) θ k = θ k − 1 − v k \theta_k=\theta_{k-1}-v_k θ k = θ k − 1 − v k
动量项𝛾 一般设为0.9。可理解为“摩擦”效果,速度的逐渐增加是作为梯度的移动平均
class Momentum : def __init__ (self, lr=0.01 , momentum=0.9 ): self.lr = lr self.momentum = momentum self.v = None def update (self, params, grads ): if self.v is None : self.v = {} for key, val in params.items(): self.v[key] = np.zeros_like(val) for key in params.keys(): self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] params[key] += self.v[key]
NAG是为动量项提供预知能力的一种方法。
v k = γ v k − 1 + η ▽ J ( θ k − 1 − γ v k − 1 ) , γ ∈ ( 0 , 1 ) v_k=\gamma v_{k-1}+\eta\triangledown J(\theta{k-1}-\gamma v_{k-1}), \gamma\in(0,1) v k = γ v k − 1 + η ▽ J ( θ k − 1 − γ v k − 1 ) , γ ∈ ( 0 , 1 ) θ k = θ k − 1 − v k \theta_k=\theta_{k-1}-v_k θ k = θ k − 1 − v k
class Nesterov : def __init__ (self, lr=0.01 , momentum=0.9 ): self.lr = lr self.momentum = momentum self.v = None def update (self, params, grads ): if self.v is None : self.v = {} for key, val in params.items(): self.v[key] = np.zeros_like(val) for key in params.keys(): self.v[key] *= self.momentum self.v[key] -= self.lr * grads[key] params[key] += self.momentum * self.momentum * self.v[key] params[key] -= (1 + self.momentum) * self.lr * grads[key]
Adagrad对不同的参数调整使用不同的学习率,学习率衰减(learning rate decay)
对非频繁出现特征相关的参数执行较大的更新(即较大的学习率)
对频繁出现特征相关的参数执行较小的学习率(即较小的学习率)
g t , i = ▽ J ( θ i , t ) g_{t,i}=\triangledown J(\theta_{i,t}) g t , i = ▽ J ( θ i , t ) θ t + 1 , j = θ t , i − η G t , i i + ε ⋅ g t , i \theta_{t+1,j}=\theta{t,i}-\frac{\eta}{\sqrt{G_{t,ii}+\varepsilon}}\cdot g_{t,i} θ t + 1 , j = θ t , i − G t , i i + ε η ⋅ g t , i
𝐺𝑡是一个对角矩阵,其每一个对角元素是到时间𝑡的梯度的平方之和,即∑ i = 1 t g i 2 \sum^{t}_{i=1}g^2_i ∑ i = 1 t g i 2
𝜖 是一个平滑项以避免除以零(通常大小为 1𝑒 − 8).
缺点:分母的梯度平方逐步累计变大,可导致学习率不断收缩,收敛变慢,从而失去学习能力
class AdaGrad : def __init__ (self, lr=0.01 ): self.lr = lr self.h = None def update (self, params, grads ): if self.h is None : self.h = {} for key, val in params.items(): self.h[key] = np.zeros_like(val) for key in params.keys(): self.h[key] += grads[key] * grads[key] params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7 )
RMSProp是一个未正式发表的自适应学习率方法;由Geoff Hinton提出
E [ g 2 ] t = 0.9 E [ g 2 ] t − 1 + 0.1 g 2 E[g^2]_t=0.9E[g^2]_{t-1}+0.1g^2 E [ g 2 ] t = 0 . 9 E [ g 2 ] t − 1 + 0 . 1 g 2 θ t + 1 = θ t − 1 E [ g 2 ] t + ε g t \theta_{t+1}=\theta_{t}-\frac{1}{\sqrt{E[g^2]_t+\varepsilon}}g_t θ t + 1 = θ t − E [ g 2 ] t + ε 1 g t Hinton建议𝛾 设为 0.9, 学习率𝜂 的默认值为0.001
RMSProp方法并不是将过去所有的梯度一视同仁地相加,而是逐渐地遗忘过去的梯度,在做加法运算时将新梯度的信息更多地反映出来。即采用“指数移动平均”:最近 1/(1 − 𝛾) 个时间步的小批量随机梯度平方项的加权平均。
class RMSprop : def __init__ (self, lr=0.01 , decay_rate = 0.99 ): self.lr = lr self.decay_rate = decay_rate self.h = None def update (self, params, grads ): if self.h is None : self.h = {} for key, val in params.items(): self.h[key] = np.zeros_like(val) for key in params.keys(): self.h[key] *= self.decay_rate self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key] params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7 )
Adam是另外一种为每一参数计算自适应学习率的方法,除了像Adadelta和RMSprop存储过去梯度平方的指数衰减平均值𝑣𝑡, Adam也保留了过去梯度的指数衰减平均值𝑚𝑡, 类似动量
m t = β 1 m t − 1 + ( 1 − β 1 ) g t m_t=\beta_1m_{t-1}+(1-\beta_1)g_t m t = β 1 m t − 1 + ( 1 − β 1 ) g t
v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 v_t=\beta_2v_{t-1}+(1-\beta_2)g_t^2 v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2
𝑚𝑡 和𝑣𝑡分别是一阶矩(均值) 和梯度二阶矩(有偏方差) 的估计值,含有偏差校正(bias-corrected) 的一阶矩和二阶矩 的估计:m ^ t = m t 1 − β 1 t \hat{m}_t=\frac{m_t}{1-\beta_1^t} m ^ t = 1 − β 1 t m t v ^ t = v t 1 − β 2 t \hat{v}_t=\frac{v_t}{1-\beta_2^t} v ^ t = 1 − β 2 t v t
参数 𝛽1、 𝛽2 ∈ [0, 1) 控制了这些移动均值(moving average)指数衰减率。
更新规则θ t + 1 = θ t − η v ^ t + ε m ^ t \theta_{t+1}=\theta{t}-\frac{\eta}{\sqrt{\hat{v}_t}+\varepsilon}\hat{m}_t θ t + 1 = θ t − v ^ t + ε η m ^ t
Adam 的核心在于用指数滑动平均去估计梯度每个分量的一阶矩(动量)和二阶矩(用于自适应学习率),并用二阶矩去归一化一阶矩,得到每一步的更新量。通常而言, Adam是自适应学习率算法的较优选择
class Adam : def __init__ (self, lr=0.001 , beta1=0.9 , beta2=0.999 ): self.lr = lr self.beta1 = beta1 self.beta2 = beta2 self.iter = 0 self.m = None self.v = None def update (self, params, grads ): if self.m is None : self.m, self.v = {}, {} for key, val in params.items(): self.m[key] = np.zeros_like(val) self.v[key] = np.zeros_like(val) self.iter += 1 lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter) for key in params.keys(): self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key]) self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key]) params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7 )
误差逆传播(error BackPropagation,简称BP)它是迄今为止最成功的神经网络学习算法,现实任务中使用神经网络时,大多在使用BP算法进行训练多层前馈神经网络,还可用于训练例如递归神经网络。
y = g ( x ) y=g(x) y = g ( x ) z = h ( y ) z=h(y) z = h ( y ) x = g ( s ) x=g(s) x = g ( s ) y = h ( s ) y=h(s) y = h ( s ) z = k ( x , y ) z=k(x,y) z = k ( x , y )
∇ s → ∇ x , ∇ y → ∇ z \nabla{s}\rightarrow\nabla{x},\nabla{y}\rightarrow\nabla{z}
∇ s → ∇ x , ∇ y → ∇ z
d z d s = d z d x d x d s + d z d y d y d s \frac{dz}{ds}=\frac{dz}{dx}\frac{dx}{ds}+\frac{dz}{dy}\frac{dy}{ds}
d s d z = d x d z d s d x + d y d z d s d y
给定训练集:D = ( ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . . ( x m , y m ) ) , x ∈ R d , y ∈ R l , D=((x_1,y_1),(x_2,y_2)....(x_m,y_m)),x∈\Bbb{R}^d,y∈\Bbb{R}^l, D = ( ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . . ( x m , y m ) ) , x ∈ R d , y ∈ R l ,
输入:d维特征向量,(d个属性);
输出:L个输出值(l维实值向量);
隐层:假定使用q个隐层神经元;
输出层权重:w i j w_{ij} w i j v i j v_{ij} v i j θ i θ_i θ i γ i γ_i γ i
隐层输入a h = ∑ i = 1 d w h j x i a_h=\sum^{d}_{i=1}{w_{hj}x_i} a h = ∑ i = 1 d w h j x i
输出层输入β j = ∑ h = 1 q w h j b h \beta_j=\sum^{q}_{h=1}{w_{hj}b_h} β j = ∑ h = 1 q w h j b h
隐层第h个神经元输出:bh;
假定功能单元均使用Sigmoid函数 。
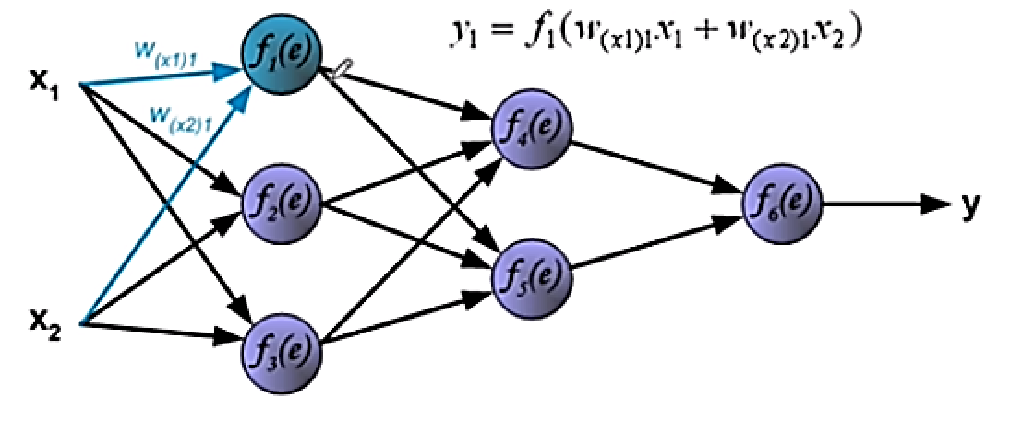
w j k l w_{jk}^l w j k l w代表权重,l代表层数,k代表第l-1层的神经元编号,j代表第l层神经元编号
对训练( x k , y k ) (x_k,y_k) ( x k , y k )
P 1 1 = f 1 ( w 11 1 x 1 + w 12 1 x 2 ) P_{1}^1=f_1(w_{11}^1x_1+w_{12}^1x_2) P 1 1 = f 1 ( w 1 1 1 x 1 + w 1 2 1 x 2 )
P 2 1 = f 2 ( w 21 1 x 1 + w 22 1 x 2 ) P_{2}^1=f_2(w_{21}^1x_1+w_{22}^1x_2) P 2 1 = f 2 ( w 2 1 1 x 1 + w 2 2 1 x 2 )
P 3 1 = f 3 ( w 31 1 x 1 + w 32 1 x 2 ) P_{3}^1=f_3(w_{31}^1x_1+w_{32}^1x_2) P 3 1 = f 3 ( w 3 1 1 x 1 + w 3 2 1 x 2 )
P 1 2 = f 4 ( w 11 2 P 1 1 + w 12 1 P 2 1 + w 13 2 P 3 1 ) P_{1}^2=f_4(w_{11}^2P_{1}^1+w_{12}^1P_{2}^1+w_{13}^2P_{3}^1) P 1 2 = f 4 ( w 1 1 2 P 1 1 + w 1 2 1 P 2 1 + w 1 3 2 P 3 1 )
P 2 2 = f 5 ( w 21 2 P 1 1 + w 22 1 P 2 1 + w 23 2 P 3 1 ) P_{2}^2=f_5(w_{21}^2P_{1}^1+w_{22}^1P_{2}^1+w_{23}^2P_{3}^1) P 2 2 = f 5 ( w 2 1 2 P 1 1 + w 2 2 1 P 2 1 + w 2 3 2 P 3 1 )
输出为:y = f 6 ( w 11 3 P 1 2 + w 12 3 P 2 2 ) y=f6(w_{11}^3P_1^2+w_{12}^3P_2^2) y = f 6 ( w 1 1 3 P 1 2 + w 1 2 3 P 2 2 )
矩阵形式:
z k × 1 l + 1 = w k × j l + 1 ⋅ a j × 1 l + b k × 1 l + 1 z^{l+1}_{k\times 1}=w^{l+1}_{k\times j}\cdot a^{l}_{j\times 1}+b^{l+1}_{k\times 1}
z k × 1 l + 1 = w k × j l + 1 ⋅ a j × 1 l + b k × 1 l + 1
a k × 1 l + 1 = σ ( z k × 1 l + 1 ) a^{l+1}_{k\times 1}=\sigma(z^{l+1}_{k\times 1})
a k × 1 l + 1 = σ ( z k × 1 l + 1 )
则网络在( x k , y k ) (x_k,y_k) ( x k , y k ) E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) 2 E_k=\frac{1}{2}\sum^{l}_{j=1}{(\hat{y}^k_j-y^k_j)^2} E k = 2 1 ∑ j = 1 l ( y ^ j k − y j k ) 2
BP通过迭代学习,在每一轮采用广义的感知机学习规划对参数进行更新估计:v ← v + △ v v\leftarrow v+\triangle v v ← v + △ v
BP算法基于梯度下降策略(gradient descent),以目标负梯度方向对参数进行调整。对于误差Ek,给定学习率:η ∈ ( 0 , 1 ) \eta \in(0,1) η ∈ ( 0 , 1 )
更新权重公式为:w 11 3 = w + △ w = w + η − y w 11 3 w_{11}^3=w+\triangle w=w+\eta -\frac{y}{w_{11}^3} w 1 1 3 = w + △ w = w + η − w 1 1 3 y
损失函数为J ( θ ) J(\theta) J ( θ )
∂ J ∂ w 11 3 = ∂ J ∂ y ⋅ ∂ y ∂ w 11 3 \frac{\partial{J}}{\partial w_{11}^3}=\frac{\partial J}{\partial y}\cdot\frac{\partial y}{\partial w_{11}^3} ∂ w 1 1 3 ∂ J = ∂ y ∂ J ⋅ ∂ w 1 1 3 ∂ y
∂ J ∂ w 12 3 = ∂ J ∂ y ⋅ ∂ y ∂ w 12 3 \frac{\partial{J}}{\partial w_{12}^3}=\frac{\partial J}{\partial y}\cdot\frac{\partial y}{\partial w_{12}^3} ∂ w 1 2 3 ∂ J = ∂ y ∂ J ⋅ ∂ w 1 2 3 ∂ y
∂ J ∂ w 23 2 = ∂ J ∂ y ∂ y ∂ P 2 2 ∂ P 2 2 ∂ w 23 2 \frac{\partial J}{\partial w_{23}^2}=\frac{\partial J}{\partial y}\frac{\partial y}{\partial P_2^2}\frac{\partial P_2^2}{\partial w_{23}^2}
∂ w 2 3 2 ∂ J = ∂ y ∂ J ∂ P 2 2 ∂ y ∂ w 2 3 2 ∂ P 2 2
其余的推导类似,利用链式法则将每个神经元的求导值、输入值都记录下来,使用动态规划的思想,可以使更新权重计算大大加快。
矩阵形式l}=\triangledown_a C\odot\sigma’(z^l)$$
误差项-中间层:$$\sigma^l_j=\frac{\partial C}{\partial z_j^l}=\sum_k{\frac{\partial C}{\partial z_k^{l+1}}\cdot\frac{\partial z_k^{l+1}}{\partial z_k^l}}=\sum_k{\frac{\partial C}{\partial z_k^{l+1}}\cdot\frac{\partial z_k^{l+1}}{\partial a_j^l}\cdot\frac{\partial a_j^l}{\partial z_kl}}=(w {l+1}{j\times k})^T\odot \sigma’(z^l) {j\times 1}$$
w矩阵:$$\frac{\partial C}{\partial w^{l+1}{kj}}=\frac{\partial C}{\partial z^{l+1} {k}}\cdot\frac{\partial z^{l+1}{k}}{\partial w{l+1}_{kj}}=\sigma {l+1} {k}\cdot\frac{\sum_j{w{l+1}_{kj}a_j l+b{l+1}_{k}}}{w {l+1}{kj}}=\sigma^{l+1} {k}\cdot a{l}_{j}=\sigma {l+1}_{k}\cdot (a{l}_{j}) T$$
b矩阵:$$\frac{\partial C}{\partial b{l+1}_{k}}=\sigma {l+1}{k}\cdot\frac{\partial z^{l+1} {k}}{\partial b{l+1}_{k}}=\sigma {l+1}_{k}$$
方程
求导
f ( x ) = x f(x)=x f ( x ) = x f ′ ( x ) = 1 f'(x)=1 f ′ ( x ) = 1
f ( x ) = 0 i f x < 0 e l s e 1 f(x)=0 if\;x<0\;else\;1 f ( x ) = 0 i f x < 0 e l s e 1 f ′ ( x ) = 0 f'(x)= 0 f ′ ( x ) = 0
f ( x ) = s i g m o i d ( x ) = 1 1 + e − x f(x)=sigmoid(x)=\frac{1}{1+e^{-x}} f ( x ) = s i g m o i d ( x ) = 1 + e − x 1 f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x)=f(x)(1-f(x)) f ′ ( x ) = f ( x ) ( 1 − f ( x ) )
f ( x ) = r e l u ( x ) f(x)=relu(x) f ( x ) = r e l u ( x ) f ′ ( x ) = 0 i f x < 0 e l s e 1 f'(x)=0\;if\;x<0\;else\;1 f ′ ( x ) = 0 i f x < 0 e l s e 1
t a n h ( x ) tanh(x) t a n h ( x ) t a n h ′ ( x ) = 1 − t a n h ( x ) 2 tanh'(x)=1-tanh(x)^2 t a n h ′ ( x ) = 1 − t a n h ( x ) 2
f ( x ) = s o f t m a x ( x ) = e x i ∑ j = 1 J e x j f(x)=softmax(x)=\frac{e^{x_i}}{\sum_{j=1}^{J}{e^{x_j}}} f ( x ) = s o f t m a x ( x ) = ∑ j = 1 J e x j e x i ∂ f i ( x ) ∂ x j = f i ( x ) ( δ i j − f j ( x ) ) \frac{\partial f_i(x)}{\partial x_j}=f_i(x)(\delta_{ij}-f_j(x)) ∂ x j ∂ f i ( x ) = f i ( x ) ( δ i j − f j ( x ) ) δ i j = 1 i f i = = j e l s e 0 \delta_{ij}=1\;if\;i==j\;else\;0 δ i j = 1 i f i = = j e l s e 0
主要目标:最小化训练集D上的累计误差 。前面算法更新规则是基于单个Ek推导的,也称作“标准BP算法”。若使用基于累计误差最小化的更新规则,成为累计误差逆传播算法(accumulated errror backpropagation)。两者都很常用:
算法
说明
标准BP算法
1、每次针对单个训练样例更新权值与阈值;
累计BP算法
1、其优化目标是最小化整个训练集上的累计误差;
累计BP算法更新频率低,防止不同样例导致训练出现抵消的现象。在很多任务中,累计误差下降到一定程度后,进一步下降会非常缓慢,这是标准BP算法往往会获得较好的解,尤其当训练集非常大时效果更明显。
均值归一化(batch normalization):随着网络的深度增加,每层特征值分布会逐渐的向激活函数的输出区间的上下两端(激活函数饱和区间)靠近,这样继续下去就会导致梯度消失。BN就是通过方法将该层特征值分布重新拉回标准正态分布,特征值将落在激活函数对于输入较为敏感的区间,输入的小变化可导致损失函数较大的变化,使得梯度变大,避免梯度消失,同时也可加快收敛。
过程:input={x1,x2,x3…xn}
计算 x1-xn的均值u
计算x1-xn的方差v
每个x i = ( x i − u ) / ( s q r t ( v 2 ) + e ) x_i = (x_i - u) / (sqrt(v^2)+ e) x i = ( x i − u ) / ( s q r t ( v 2 ) + e )
在对结果进行scale于shift操作 x i = s c a l e ∗ x i + s h i f t x_i = scale*x_i + shift x i = s c a l e ∗ x i + s h i f t
第四步存在的原因是batch_normal后,数据趋向标准正态,会导致网络表达能力变差,这里加入后标准正态分布有些偏移,变得不那么标准了。这两个参数时学习而来。
优点:减少梯度消失,加快了收敛过程。起到类似dropout一样的正则化能力,一定程度上防止过拟合。放宽了一定的调参要求。可以替代LRN。
缺点:需要计算均值与方差,不适合动态网络或者RNN。计算均值方差依赖每批次,因此数据最好足够打乱。
全零初始化 :无法进行模型训练
随机初始化:使用小的随机数(高斯分布,零均值, 1e-2标准差)初始化。小网络可以,对于深度网络有问题 。网络输出数据分布的方差会随着神经元的个数而改变。
Xavier初始化:保证前向传播和反向传播时每一层的方差一致。根据每层的输入个数和输出个数来决定。参数随机初始化的分布范围。高斯分布的权重初始化为: 高斯分布的随机数乘上2 n i n + n o u t \frac{\sqrt{2}}{\sqrt{n_{in}+n_{out}}} n i n + n o u t 2
He参数初始化:对Xavier方法的改进,将ReLU非线性映射造成的影响考虑进参数初始化中。高斯分布的权重初始化为: 高斯分布的随机数乘上2 n i n \frac{\sqrt{2}}{\sqrt{n_{in}}} n i n 2
一般情况下,偏置设为0
w = np.random.randn(node_num, node_num) * 1 w = np.random.randn(node_num, node_num) * 0.01 w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num) w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)
超参数包括:网络模型(结构、层数、激活函数等)、学习率、批次大小(batch size)、迭代次数 (epoch, iteration)、优化器
通过交叉验证方法调整超参,将训练数据集分为:数据集+验证集,通过验证集结果来调整超参。划分方法分为:hold-out,k-fold
早停early stopping :
将训练数据分为训练集和验证集。训练集计算梯度和更新,验证估计误差。
若训练误差连续a轮的变化小于b,则停止训练
使用验证集:若训练误差降低,验证误差升高,则停止训练。
返回具有最小验证误差的链接权重和阈值。
dropout可以看做是一种集成学习的方式。通过随机失活神经元,将不同网络分别训练,再进行结合。
训练阶段:以概率𝑝随机移除网络中的神经元结点以及与之相连的所有输入和输出边
测试阶段: 所有神经元处于激活态,但用系数(1 − 𝑝) 减少激活值来补偿训练时丢弃的激活
class Dropout : def __init__ (self, dropout_ratio=0.5 ): self.dropout_ratio = dropout_ratio self.mask = None def forward (self, x, train_flg=True ): if train_flg: self.mask = np.random.rand(*x.shape) > self.dropout_ratio return x * self.mask else : return x * (1.0 - self.dropout_ratio) def backward (self, dout ): return dout * self.mask
regularization在误差目标函数中,增加一项描述网络复杂度:例如连接权和阈值的平方和
误差目标函数增加正则化项,用于对经验误差和网络复杂度进行折中。偏好比较小的连接权和阈值,使网络输出更“光滑”
l2范数正则化:J ( θ ) = J ( θ ) + λ 2 m ∑ ∥ w ∥ 2 J(\theta)=J(\theta)+\frac{\lambda}{2m}\sum{\left \| w \right \| }^2 J ( θ ) = J ( θ ) + 2 m λ ∑ ∥ w ∥ 2 l a m b d a lambda l a m b d a
l1范数正则化:J ( θ ) = J ( θ ) + λ 2 m ∑ ∥ w ∥ J(\theta)=J(\theta)+\frac{\lambda}{2m}\sum{\left \| w \right \| } J ( θ ) = J ( θ ) + 2 m λ ∑ ∥ w ∥
RBF(Radial Basis Function,径向基函数)网络在分类任务中除BP之外最常用的一种
使用径向基函数作为隐层神经元激活函数ρ: ,定义为样本x到数据中心ci之间欧式距离的单调函数,常用高斯径向基函数。 。ci表示隐层神经元对应的中心、wi表示权重。
输出层是隐层神经元输出的线性组合
确定神经元中心ci,常用的方式包括随机采样、聚类等
利用BP算法等确定参数wi和βi。
ART(Adaptive Resonance Theory,自适应谐振理论)竞争学习的代表,是一种常用的无监督学习策略。该策略网络输出神经元相互竞争,每一时刻仅有一个竞争获胜的神经元被激活。其他神经元被抑制。包含比较层、识别层、识别阈值和重置模块。
SOM(Self-Organizing Map,自组织映射)网络是最常用的聚类方法之一:
竞争型的无监督神经网络
将高维数据映射到低维空间,并保持输入数据在高维空间的拓扑结构。即将高维空间中相似的样本点映射到网络输出层中邻近神经元
每个神经元拥有一个权向量
目标:为每个输出层神经元找到合适的权向量以保持拓扑结构
训练
网络接收输入样本后,将会确定输出层的“获胜”神经元(“胜者通吃”)
获胜神经元的权向量将向当前输入样本移动
构造性神经网络:将网络结构也当做学习的目标,并在训练过程中找到最符合的网络结构。是结构自适应网络的重要代表。
训练
开始时只有输入层和输出层
级联(Cascade):新的隐层节点逐渐加入,从而创建起层级结构
相关(Correlation):最大化新节点的输出与网络误差之间的相关性
网络可以有环形结构,可让使一些神经元的输出反馈回来最为输入
t 时刻网络的输出状态: 由 t 时刻的输入状态和 t-1时刻的网络状态共同决定
Elman网络是最常用的递归神经网络之一
结构与前馈神经网络很相似,但隐层神经元的输出被反馈回来
使用推广的BP算法训练