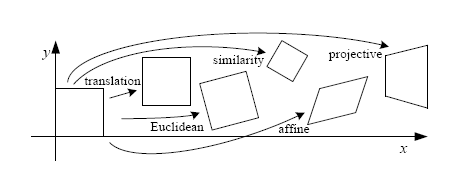
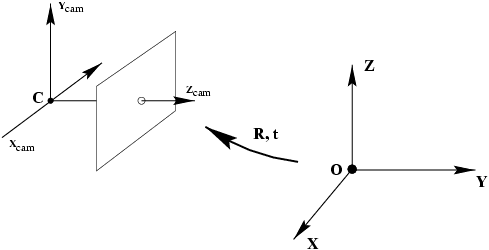
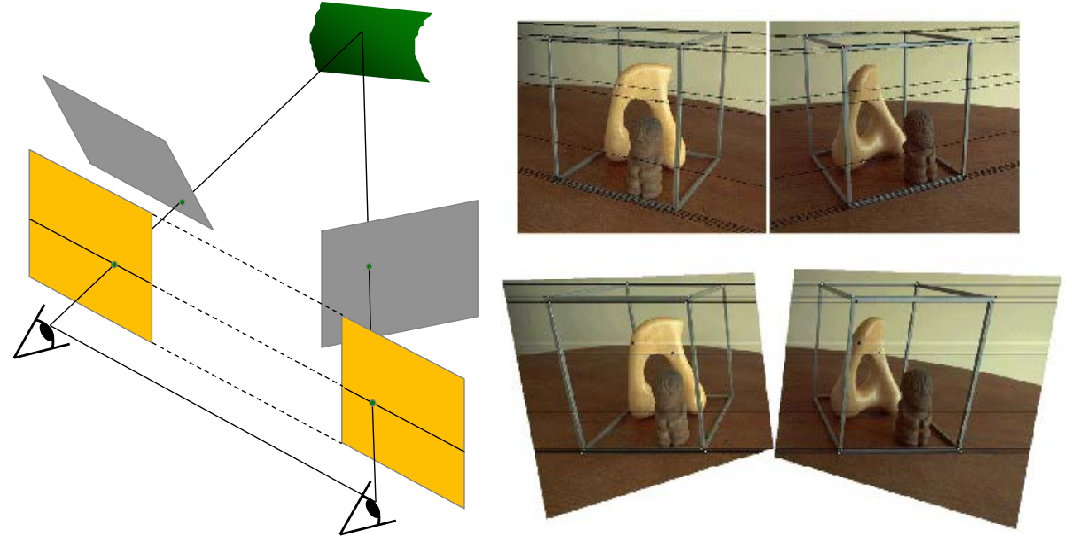
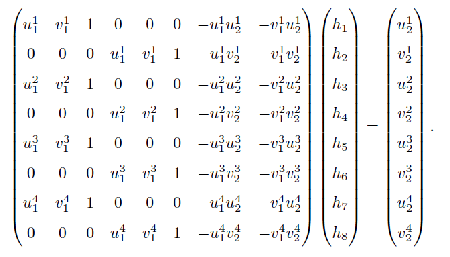图像变换的方式:translation(平移), rotation(旋转), aspect(两边不等比例放缩), affine(保持平行关系), perspective(四边不等比例放缩)
变换
说明
矩阵
自由度数量
Translation
平移:位置变化,大小不变
2,位置
Euclidean
欧几里得:位置和旋转变化,大小不变
[ R t 0 T 1 ] \begin{bmatrix} R & t \\ 0^T & 1 \end{bmatrix} [ R 0 T t 1 ] 3,位置+旋转
Similarity
放缩:大小和旋转变化
[ s R t 0 T 1 ] \begin{bmatrix} sR & t \\ 0^T & 1 \end{bmatrix} [ s R 0 T t 1 ] 4,位置+旋转+缩放
Affine
仿射:保持平行关系
[ A t 0 T 1 ] \begin{bmatrix} A & t \\ 0^T & 1 \end{bmatrix} [ A 0 T t 1 ] 6
Projective
投影:相机的结果,只保持直线形态不变
[ A t v T 1 ] \begin{bmatrix} A & t \\ v^T & 1 \end{bmatrix} [ A v T t 1 ] 8
Homography
单应性:Projective的一种,描述两个二维平面变换
8,虽然是9个未知数但是h 22 h_{22} h 2 2
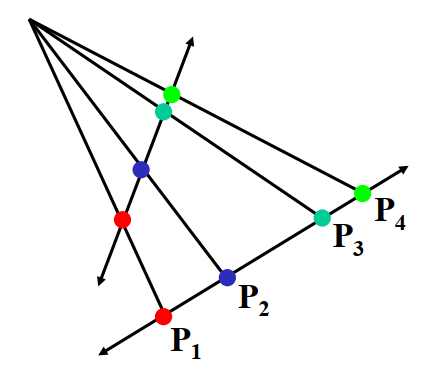
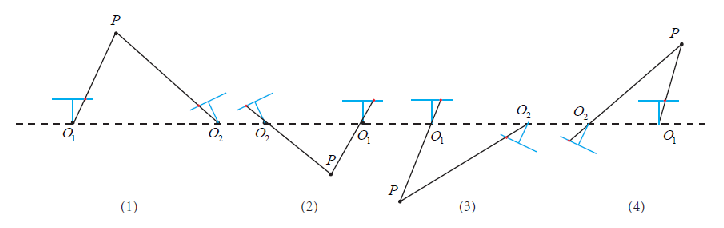
t = ∣ ∣ P 3 − P 1 ∣ ∣ ∣ ∣ P 4 − P 2 ∣ ∣ ∣ ∣ P 3 − P 2 ∣ ∣ ∣ ∣ P 4 − P 1 ∣ ∣ t = \frac{||P_3-P_1||||P_4-P_2||}{||P_3-P_2||||P_4-P_1||} t = ∣ ∣ P 3 − P 2 ∣ ∣ ∣ ∣ P 4 − P 1 ∣ ∣ ∣ ∣ P 3 − P 1 ∣ ∣ ∣ ∣ P 4 − P 2 ∣ ∣ 原理证明
单应性矩阵的限制
单应性矩阵描述的两张图片的变换,只能是平面和平面。
只能应用于固定光心纯旋转的相机拍摄的两个平面,否则会出现歧义
定义
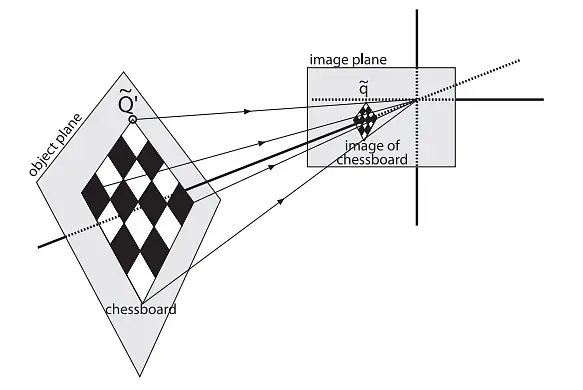
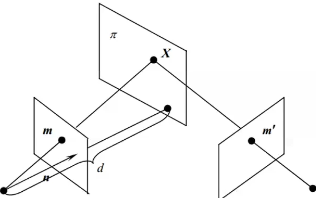
在计算机视觉中,平面的单应性被定义为一个平面到另外一个平面的投影映射。因此一个二维平面上的点映射到摄像机成像仪上的映射就是平面单应性的例子。如果使用齐次坐标将标定板上一点P 映射到成像仪上的点m的,这种映射可以用所谓的单应性矩阵来表示。
不损失一般性,可以将标定板平面定义为世界坐标系的Z = 0平面:s [ x i ′ y i ′ 1 ] = A [ R t ] [ x i y i z i 1 ] = A [ r 1 r 2 r 3 t ] [ x i y i 0 1 ] = A [ r 1 r 2 t ] [ x i y i 1 ] s\begin{bmatrix} x_i^\prime \\ y_i^\prime \\1\end{bmatrix}= A\begin{bmatrix} R & t \end{bmatrix}\begin{bmatrix} x_i \\ y_i \\ z_i \\1\end{bmatrix}= A\begin{bmatrix} r_1 &r_2 &r_3 & t \end{bmatrix}\begin{bmatrix} x_i \\ y_i \\ 0 \\1\end{bmatrix}= A\begin{bmatrix} r_1 &r_2 & t \end{bmatrix}\begin{bmatrix} x_i \\ y_i \\1\end{bmatrix} s ⎣ ⎡ x i ′ y i ′ 1 ⎦ ⎤ = A [ R t ] ⎣ ⎢ ⎢ ⎡ x i y i z i 1 ⎦ ⎥ ⎥ ⎤ = A [ r 1 r 2 r 3 t ] ⎣ ⎢ ⎢ ⎡ x i y i 0 1 ⎦ ⎥ ⎥ ⎤ = A [ r 1 r 2 t ] ⎣ ⎡ x i y i 1 ⎦ ⎤
多出的1表示齐次坐标系
其中 s 为一尺度因数,H = A [ r 1 r 2 t ] H = A \begin{bmatrix} r_1 &r_2 & t \end{bmatrix} H = A [ r 1 r 2 t ] [ R t ] \begin{bmatrix} R & t \end{bmatrix} [ R t ]
因为使用了齐次坐标,给定一个单应H,给它的元素乘上同一个数a,得到的的单应a*H和H作用相同,因为新单应无非把齐次点x1变成了齐次点a*x1, 在其次坐标下表示同一个点。因此我们可以把a换成1/h22,那么H就变成了只有8个自由元素的矩阵。
单应性变换Homography:[ x i ′ y i ′ 1 ] ≅ [ h 00 h 01 h 02 h 10 h 11 h 12 h 20 h 21 h 22 ] [ x i y i 1 ] \begin{bmatrix} x_i^\prime \\ y_i^\prime \\1\end{bmatrix}\cong \begin{bmatrix} h_{00} & h_{01} & h_{02} \\h_{10} & h_{11} & h_{12} \\h_{20} & h_{21} & h_{22}\end{bmatrix}\begin{bmatrix} x_i \\ y_i \\1\end{bmatrix} ⎣ ⎡ x i ′ y i ′ 1 ⎦ ⎤ ≅ ⎣ ⎡ h 0 0 h 1 0 h 2 0 h 0 1 h 1 1 h 2 1 h 0 2 h 1 2 h 2 2 ⎦ ⎤ ⎣ ⎡ x i y i 1 ⎦ ⎤ λ p = H Q \lambda p=HQ λ p = H Q
求解
x i ′ = h 00 x i + h 01 y i + h 02 h 20 x i + h 21 y i + h 22 x_i^\prime=\frac{h_{00}x_i+h_{01}y_i+h_{02}}{h_{20}x_i+h_{21}y_i}+h_{22} x i ′ = h 2 0 x i + h 2 1 y i h 0 0 x i + h 0 1 y i + h 0 2 + h 2 2 x i ′ ( h 20 x i + h 21 y i + h 22 ) = h 00 x i + h 01 y i + h 02 x_i^\prime(h_{20}x_i+h_{21}y_i+h_{22})={h_{00}x_i+h_{01}y_i+h_{02}} x i ′ ( h 2 0 x i + h 2 1 y i + h 2 2 ) = h 0 0 x i + h 0 1 y i + h 0 2
y i ′ = h 10 x i + h 11 y i + h 12 h 20 x i + h 21 y i + h 22 y_i^\prime=\frac{h_{10}x_i+h_{11}y_i+h_{12}}{h_{20}x_i+h_{21}y_i+h_{22}} y i ′ = h 2 0 x i + h 2 1 y i + h 2 2 h 1 0 x i + h 1 1 y i + h 1 2 y i ′ ( h 20 x i + h 21 y i + h 22 ) = h 10 x i + h 11 y i + h 12 y_i^\prime(h_{20}x_i+h_{21}y_i+h_{22})={h_{10}x_i+h_{11}y_i+h_{12}} y i ′ ( h 2 0 x i + h 2 1 y i + h 2 2 ) = h 1 0 x i + h 1 1 y i + h 1 2
结合得到:[ x i y i 1 0 0 0 − x i ′ x i − x i ′ y i − x i ′ 0 0 0 x i y i 1 − y i ′ x i − y i ′ y i − y i ′ ] [ h 00 h 01 h 02 h 10 h 11 h 12 h 20 h 21 h 22 ] = [ 0 0 ] \begin{bmatrix} x_i&y_i &1&0&0&0&-x_i^\prime x_i&-x_i^\prime y_i&-x_i^\prime \\0&0&0&x_i&y_i &1&-y_i^\prime x_i&-y_i^\prime y_i&-y_i^\prime \end{bmatrix}\begin{bmatrix} h_{00}\\h_{01}\\h_{02}\\h_{10}\\h_{11}\\h_{12}\\h_{20}\\h_{21}\\h_{22} \end{bmatrix}=\begin{bmatrix} 0\\0 \end{bmatrix} [ x i 0 y i 0 1 0 0 x i 0 y i 0 1 − x i ′ x i − y i ′ x i − x i ′ y i − y i ′ y i − x i ′ − y i ′ ] ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ h 0 0 h 0 1 h 0 2 h 1 0 h 1 1 h 1 2 h 2 0 h 2 1 h 2 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = [ 0 0 ]
那么需要多少个点对求解这个H呢?如果需要唯一解的话,需要4个点对(对应8个方程,去解H中的8个未知数)。由于无法获得准确的x,y,所以通过多个点求解矩阵
[ x 1 y 1 1 0 0 0 − x 1 ′ x 1 − x 1 ′ y 1 − x 1 ′ 0 0 0 x 1 y 1 1 − y 1 ′ x 1 − y 1 ′ y 1 − y 1 ′ ⋮ x n y n 1 0 0 0 − x n ′ x n − x n ′ y n − x n ′ 0 0 0 x n y n 1 − y n ′ x n − y n ′ y n − y n ′ ] [ h 00 h 01 h 02 h 10 h 11 h 12 h 20 h 21 h 22 ] = [ 0 0 ] = A 2 n × 9 ⋅ h 9 = 0 2 n \begin{bmatrix} x_1&y_1 &1&0&0&0&-x_1^\prime x_1&-x_1^\prime y_1&-x_1^\prime \\0&0&0&x_1&y_1 &1&-y_1^\prime x_1&-y_1^\prime y_1&-y_1^\prime\\&&&&&\vdots\\x_n&y_n &1&0&0&0&-x_n^\prime x_n&-x_n^\prime y_n&-x_n^\prime \\0&0&0&x_n&y_n &1&-y_n^\prime x_n&-y_n^\prime y_n&-y_n^\prime \end{bmatrix}\begin{bmatrix} h_{00}\\h_{01}\\h_{02}\\h_{10}\\h_{11}\\h_{12}\\h_{20}\\h_{21}\\h_{22} \end{bmatrix}=\begin{bmatrix} 0\\0 \end{bmatrix}=A_{2n\times 9}\cdot h_9=0_{2n}
⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 0 x n 0 y 1 0 y n 0 1 0 1 0 0 x 1 0 x n 0 y 1 0 y n 0 1 ⋮ 0 1 − x 1 ′ x 1 − y 1 ′ x 1 − x n ′ x n − y n ′ x n − x 1 ′ y 1 − y 1 ′ y 1 − x n ′ y n − y n ′ y n − x 1 ′ − y 1 ′ − x n ′ − y n ′ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ h 0 0 h 0 1 h 0 2 h 1 0 h 1 1 h 1 2 h 2 0 h 2 1 h 2 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = [ 0 0 ] = A 2 n × 9 ⋅ h 9 = 0 2 n
定义最小二乘法求解:m i n i m i z e ∣ ∣ A h − 0 ∣ ∣ 2 minimize\;||Ah-0||^2 m i n i m i z e ∣ ∣ A h − 0 ∣ ∣ 2
利用SVD分解,得到h ^ \hat{h} h ^ A T A A^TA A T A
opencv计算
opencv 的findHomography 函数用于计算(估计两个平面的单应性矩阵):Mat cv::findHomography ( InputArray srcPoints, InputArray dstPoints, int method = 0, double ransacReprojThreshold = 3, OutputArray mask = noArray(), const int maxIters = 2000,const double confidence = 0.995)
method:Method used to computed a homography matrix. The following methods are possible:
如果参数method设置为默认值0,该函数使用一个简单的最小二乘方案来计算初始的单应性估计。
RANSAC求解
然而,如果不是所有的点对(srcPoints,dstPoints)都适应这个严格的透视变换。(也就是说,有一些异常值),这个初始估计值将很差。在这种情况下,我们可以使用两个鲁棒性算法中的一个。RANSCA和LMEDS这两个方法都尝试不同的随机的相对应点对的子集,每四对点集一组,使用这个子集和一个简单的最小二乘算法来估计单应性矩阵,然后计算得到单应性矩阵的质量quality/goodness。(对于RANSAC方法是内层围点的数量,对于LMeDs是中间的重投影误差)。然后最好的子集用来产生单应性矩阵的初始化估计和inliers/outliers的掩码。
RANSAC方法,几乎可以处理任含有何异常值比率的情况,但是它需要一个阈值用来区分inliers和outliers。LMeDS方法不需要任何阈值,但是它仅在inliers大于50%的情况下才能正确的工作。最后,如果你确信在你计算得到的特征点仅含一些小的噪声,但是没有异常值,默认的方法可能是最好的选择。(因此,在计算相机参数时,我们或许仅使用默认的方法)
图像畸变是由于透镜制造精度以及组装工艺的偏差会引入畸变,导致原始图像失真。对于针孔相机模型,镜头的畸变分为径向畸变和切向畸变两类。
学名
类
含义
运用
扩展变形
透视
近大远小,距离感+
近距离拍摄,广角镜头,画面有纵深感
压缩变形
透视
近小远大,距离感-
远距离拍摄,长焦镜头视角窄,画面显得近
桶形畸变
径向畸变
镜头中央区域放大比例大于边缘区
枕形畸变
径向畸变
镜头中央区域放大比例小于边缘区
切向畸变
切向畸变
摄像头感光平面和镜头不平行
使用归一化坐标变换来描述,使用极坐标系( θ , r ) (\theta,r) ( θ , r ) ( x , y ) (x,y) ( x , y ) ( x d i s t o r t e d , y d i s t o r t e d ) (x_{distorted},y_{distorted}) ( x d i s t o r t e d , y d i s t o r t e d ) k 1 , k 2 , k 3 , p 1 , p 2 k_1,k_2,k_3,p_1,p_2 k 1 , k 2 , k 3 , p 1 , p 2
径向畸变,随着远离中心点,畸变强度增加,
{ x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) \begin{cases}x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)\\y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6)\end{cases} { x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) 一般k 1 , k 2 k_1,k_2 k 1 , k 2 k 3 k_3 k 3
切向畸变
{ x d i s t o r t e d = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y \begin{cases}x_{distorted}=x+2p_1xy+p_2(r^2+2x^2)\\y_{distorted}=y+p_1(r^2+2y^2)+2p_2xy\end{cases} { x d i s t o r t e d = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y
综合考虑:上面两种畸变在现实世界中一般是同时存在的
{ x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y \begin{cases}x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)+x+2p_1xy+p_2(r^2+2x^2)\\y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6)+y+p_1(r^2+2y^2)+2p_2xy\end{cases} { x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y
三维坐标点投影到归一化平面上,确定( x , y ) (x,y) ( x , y )
对规划化的平面进行校正,得到( x d i s t o r t e d , y d i s t o r t e d ) (x_{distorted},y_{distorted}) ( x d i s t o r t e d , y d i s t o r t e d )
将确定的点通过内参数矩阵,投影到像素平面,得到该点的正确位置
{ u = f x x c o r r e c t e d + c x v = f y y c o r r e c t e d + c y \begin{cases}u=f_xx_{corrected}+c_x\\v=f_yy_{corrected}+c_y\end{cases} { u = f x x c o r r e c t e d + c x v = f y y c o r r e c t e d + c y
已知两条直线,求交点:I = x 1 × x 2 I=x_1\times x_2 I = x 1 × x 2
已知两点,求直线:x = I 1 × I 2 x=I_1\times I_2 x = I 1 × I 2
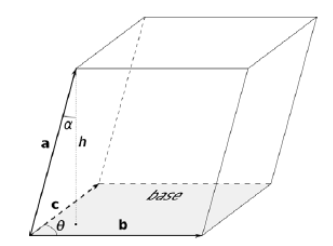
向量的混合积vector mixed product:a ⋅ ( b × c ) a\cdot(b\times c) a ⋅ ( b × c )
the volume of a parallelepiped defined by the three vectors a,b,c. three vectors a,b,c are coplanar iff a ⋅ ( b × c ) = 0 a\cdot(b\times c)=0 a ⋅ ( b × c ) = 0
abc组成的立方体的体积,当abc共面则为0
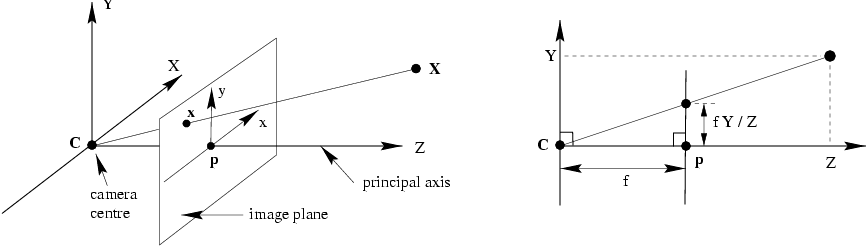
有图可以看出,以镜头为世界坐标系原点,点P(X,Y,Z)、镜头焦距f、屏幕坐标X’Y’、物体坐标XY的关系是
Z f = X X ′ = Y Y ′ \frac{Z}{f}=\frac{X}{X'}=\frac{Y}{Y'} f Z = X ′ X = Y ′ Y 上式可得出成像公式:X ′ = f X Z X'=f\frac{X}{Z} X ′ = f Z X Y ′ = f Y Z Y'=f\frac{Y}{Z} Y ′ = f Z Y
像素坐标习惯表示为一个矩阵,所以需要对屏幕坐标进行了缩放和偏移,由此可得:
屏幕坐标到像素坐标:u = α X ′ + c x u=\alpha X'+c_x u = α X ′ + c x v = β Y ′ + c y v=\beta Y'+c_y v = β Y ′ + c y
物体坐标到像素坐标,将缩放系数α β \alpha\beta α β
{ u = f x X Z + c x v = f y Y Z + c y \begin{cases}u=f_x\frac{X}{Z}+c_x\\v=f_y\frac{Y}{Z}+c_y\end{cases}
{ u = f x Z X + c x v = f y Z Y + c y
将uv转换的公式变为矩阵形式:
齐次坐标:[ u v 1 ] = 1 Z [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] : = 1 Z K P \begin{bmatrix}u\\v\\1\end{bmatrix}=\frac{1}{Z}\begin{bmatrix}f_x&&0&&c_x\\0&&f_y&&c_y\\0&&0&&1\end{bmatrix}\begin{bmatrix}X\\Y\\Z\end{bmatrix}:=\frac{1}{Z}KP ⎣ ⎡ u v 1 ⎦ ⎤ = Z 1 ⎣ ⎡ f x 0 0 0 f y 0 c x c y 1 ⎦ ⎤ ⎣ ⎡ X Y Z ⎦ ⎤ : = Z 1 K P
除掉Z的原因是,在图像中已经将深度信息丢失了,统一变为归一化坐标系的坐标。
其中的K为相机的内参矩阵K ( f x , f y , u 0 , v 0 ) K(fx,fy,u_0,v_0) K ( f x , f y , u 0 , v 0 )
相机坐标系P u v P_{uv} P u v P w P_w P w T ( R , t ) T(R,t) T ( R , t )
P u v = 1 Z K ( R P w + t ) = 1 Z K T P w P_{uv}=\frac{1}{Z}K(RP_w+t)=\frac{1}{Z}KTP_w P u v = Z 1 K ( R P w + t ) = Z 1 K T P w 这里R,t或T称为外参,是姿态估计的目标
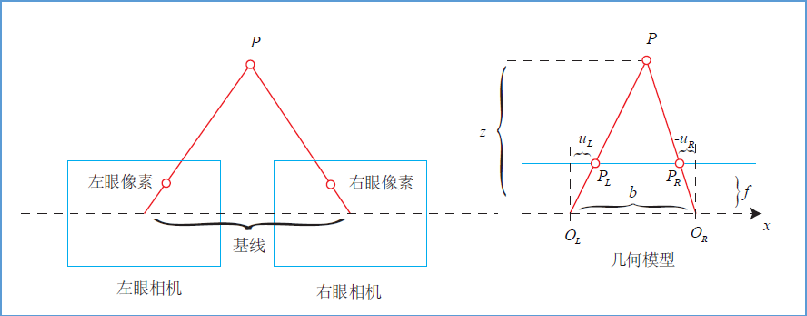
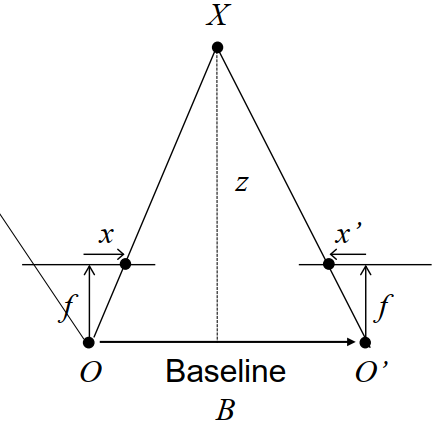
左右相机中心距离成为基线,左右像素的几何关系:
z − f z = b − u L + u R b \frac{z-f}{z}=\frac{b-u_L+u_R}{b} z z − f = b b − u L + u R
整理得
z = f b d z=\frac{fb}{d} z = d f b d = u L − u R d=u_L-u_R d = u L − u R
d称为视差(disparity),描述同一个点在左右目上成像的距离d。最小为1个像素,因此双目能测量的z有最大值:fb
虽然距离公式简单,但d不容易计算
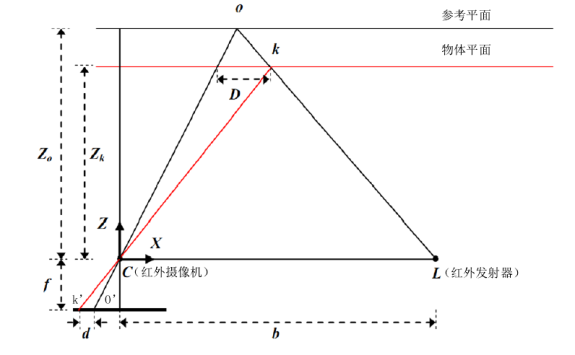
Kinect 获取深度测量的原理是三角测距原理,采用一种名为光编码技术,不同于传统的 ToF 光或者结构光测量技术,Kinect 传感器自带红外发射器和红外摄像头,不需要其他的光源,可以直接获取到深度图。
假设目标k在距传感器距离为0z的参考平面上,红外相机捕捉到目标k处的激光散斑的红外图像上成像的位置为k’。当目标的深度发生变化时,图像上的激光散斑k’沿X轴移动到o’。测量出时差d,也就是此激光散斑移动的距离。
D b = z 0 − z k z 0 \frac{D}{b}=\frac{z_0-z_k}{z_0} b D = z 0 z 0 − z k d f = D z k \frac{d}{f}=\frac{D}{z_k} f d = z k D Zk表示目标距传感器的深度,b指基线长度,f指红外相机的焦距。D是点k在空间的位移,d是在红外图像上的视差
可推导出:
z k = z 0 1 + z 0 f b d z_k=\frac{z_0}{1+\frac{z_0}{fb}d} z k = 1 + f b z 0 d z 0
若固定参量Z0,f和b已通过标定获得,则可根据式得到深度信息。在 Kinect 内部,这些深度运算已经写入到芯片中。
在现实世界中有一点P,在世界坐标系 坐标为P ( X , Y , Z ) P(X,Y,Z) P ( X , Y , Z ) 相机坐标系 坐标为Z ( u , v ) Z(u,v) Z ( u , v )
Z = ( R , t ) P Z=(R,t)P Z = ( R , t ) P 确定T = ( R , t ) T=(R,t) T = ( R , t ) 系统外参 :Z = ( R ′ , t ′ ) P Z=(R',t')P Z = ( R ′ , t ′ ) P
确定K ( f x , f y , u 0 , v 0 ) K(f_x,f_y,u_0,v_0) K ( f x , f y , u 0 , v 0 ) 相机内参 ,内参是固定的,一般相机会有标识。
图像坐标系 ( c x , c y ) (c_x,c_y) ( c x , c y ) 像素坐标系 ( u x , v y ) (u_x,v_y) ( u x , v y ) 相机到成像平面的距离也就是相机的焦距 ( f x , f y ) (f_x,f_y) ( f x , f y ) 中心 ( u 0 , v 0 ) (u_0,v_0) ( u 0 , v 0 )
K ( f x , f y , u 0 , v 0 ) = [ f x 0 c x 0 f y c y 0 0 1 ] K(fx,fy,u_0,v_0)=\begin{bmatrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix} K ( f x , f y , u 0 , v 0 ) = ⎣ ⎡ f x 0 0 0 f y 0 c x c y 1 ⎦ ⎤
假设知道内参数矩阵和在图像上的位置,那么可以根据外参矩阵求得物体在世界坐标系的位置。这就是标定 的过程。
假设相机坐标系和世界坐标系重合,已知三维坐标(X,Y,Z),根据相似三角形可知
f Z = v Y \frac{f}{Z}=\frac{v}{Y} Z f = Y v v = f Y Z v=\frac{fY}{Z} v = Z f Y u = f X Z u=\frac{fX}{Z} u = Z f X
变换矩阵:
[ X Y Z 1 ] → [ f X f Y Z ] = [ f 0 f 0 1 0 ] [ X Y Z 1 ] \begin{bmatrix} X\\Y\\Z\\1 \end{bmatrix} \rightarrow \begin{bmatrix} fX\\fY\\Z \end{bmatrix} =\begin{bmatrix} f&&&0\\&f&&0\\&&1&0 \end{bmatrix}\begin{bmatrix} X\\Y\\Z\\1 \end{bmatrix} ⎣ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎤ → ⎣ ⎡ f X f Y Z ⎦ ⎤ = ⎣ ⎡ f f 1 0 0 0 ⎦ ⎤ ⎣ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎤
相机成像平面中心在右下角时,需要平移:
[ X Y Z 1 ] → [ f X + Z p x f Y + Z p y Z ] = [ f p x 0 f p y 0 1 0 ] [ X Y Z 1 ] \begin{bmatrix} X\\Y\\Z\\1 \end{bmatrix} \rightarrow \begin{bmatrix} fX+Zp_x\\fY+Zp_y\\Z \end{bmatrix} =\begin{bmatrix} f&&p_x&0\\&f&p_y&0\\&&1&0 \end{bmatrix}\begin{bmatrix} X\\Y\\Z\\1 \end{bmatrix} ⎣ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎤ → ⎣ ⎡ f X + Z p x f Y + Z p y Z ⎦ ⎤ = ⎣ ⎡ f f p x p y 1 0 0 0 ⎦ ⎤ ⎣ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎤
最终得到内参矩阵:
K = [ f p x 0 f p y 0 1 0 ] K=\begin{bmatrix} f&&p_x&0\\&f&p_y&0\\&&1&0 \end{bmatrix} K = ⎣ ⎡ f f p x p y 1 0 0 0 ⎦ ⎤
投影矩阵P:
P = K [ R ∣ t ] P=K[R|t] P = K [ R ∣ t ] 当世界坐标系和相机坐标系重叠时R=I,t=0:P = K [ I ∣ 0 ] P=K[I|0] P = K [ I ∣ 0 ]
相机的感光尺寸长宽可能是不一致的:m x , m y m_x,m_y m x , m y 1 m x × m y \frac{1}{m_x\times m_y} m x × m y 1
K = p i x e l s m × m = [ m x m y 1 ] [ f p x 0 f p y 0 1 0 ] = [ α x β x α y β y 1 ] K=\frac{pixels}{m}\times m=\begin{bmatrix} m_x&&\\&m_y&\\&&1 \end{bmatrix}\begin{bmatrix} f&&p_x&0\\&f&p_y&0\\&&1&0 \end{bmatrix}=\begin{bmatrix} \alpha_x&&\beta_x\\&\alpha_y&\beta_y\\&&1 \end{bmatrix} K = m p i x e l s × m = ⎣ ⎡ m x m y 1 ⎦ ⎤ ⎣ ⎡ f f p x p y 1 0 0 0 ⎦ ⎤ = ⎣ ⎡ α x α y β x β y 1 ⎦ ⎤ 一般情况下m x = m y m_x=m_y m x = m y
相机标定就是确定外参K
x = K [ R t ] X x=K\begin{bmatrix} R &t \end{bmatrix}X x = K [ R t ] X [ λ x λ y λ ] = [ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ] [ X Y Z 1 ] \begin{bmatrix} \lambda x\\\lambda y\\\lambda \end{bmatrix}=\begin{bmatrix} *&*&*&*&\\*&*&*&*&\\*&*&*&*& \end{bmatrix}\begin{bmatrix} X\\Y\\Z\\1 \end{bmatrix} ⎣ ⎡ λ x λ y λ ⎦ ⎤ = ⎣ ⎡ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ⎦ ⎤ ⎣ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎤
假设在三维空间中已知n个点的世界坐标X i X_i X i x i x_i x i
线型方法:
x = P X x=PX x = P X x × P X = [ x y 1 ] × [ P 1 T X i P 2 T X i P 3 T X i ] = [ 0 − X i T y i X i T X i T 0 − x i X i T − y i T X i T x i X i T 0 ] × [ P 1 P 2 P 3 ] = 0 x\times PX=\begin{bmatrix} x\\y\\1 \end{bmatrix}\times\begin{bmatrix} P_1^TX_i\\P_2^TX_i\\P_3^TX_i \end{bmatrix}=\begin{bmatrix} 0&-X_i^T&y_iX_i^T\\X_i^T&0&-x_iX_i^T\\-y_i^TX_i^T&x_iX_i^T&0 \end{bmatrix}\times\begin{bmatrix} P_1\\P_2\\P_3 \end{bmatrix}=0 x × P X = ⎣ ⎡ x y 1 ⎦ ⎤ × ⎣ ⎡ P 1 T X i P 2 T X i P 3 T X i ⎦ ⎤ = ⎣ ⎡ 0 X i T − y i T X i T − X i T 0 x i X i T y i X i T − x i X i T 0 ⎦ ⎤ × ⎣ ⎡ P 1 P 2 P 3 ⎦ ⎤ = 0
多个已知点组合为:[ 0 − X 1 T y 1 X 1 T X 1 T 0 − x 1 X 1 T ⋮ 0 − X n T y n X n T X n T 0 − x n X n T ] × [ P 1 P 2 P 3 ] = 0 \begin{bmatrix} 0&-X_1^T&y_1X_1^T\\X_1^T&0&-x_1X_1^T\\ &\vdots\\0&-X_n^T&y_nX_n^T\\X_n^T&0&-x_nX_n^T \end{bmatrix}\times\begin{bmatrix} P_1\\P_2\\P_3 \end{bmatrix}=0 ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0 X 1 T 0 X n T − X 1 T 0 ⋮ − X n T 0 y 1 X 1 T − x 1 X 1 T y n X n T − x n X n T ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ × ⎣ ⎡ P 1 P 2 P 3 ⎦ ⎤ = 0
P有11个自由度,至少需要6个点得到精确解,同样由于特征点精度问题,需要最小二乘的方法求解最小特征值的特征向量∣ ∣ A p ∣ ∣ 2 ||Ap||^2 ∣ ∣ A p ∣ ∣ 2
线型方法只求解了P,但是没有将内外参区分。实际中使用非线性方法求解:
定义投影矩阵方程
定义损失函数,计算偏差
根据牛顿法迭代求取最小化解
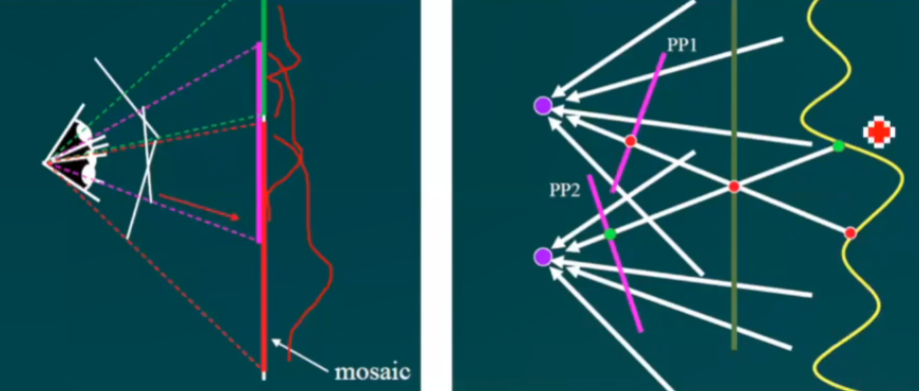
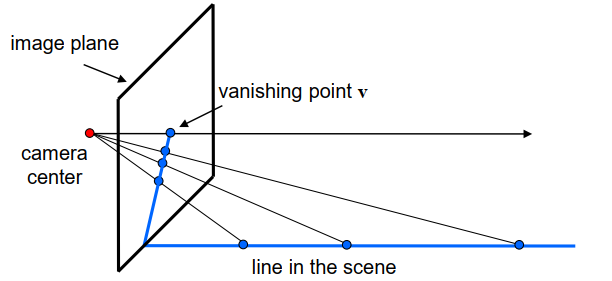
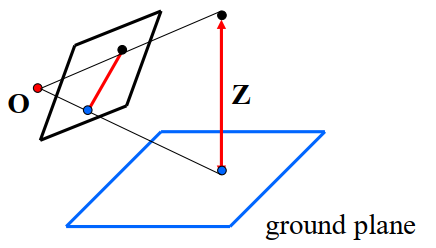
场景的一条直线的无穷远处,在相机平面会展现为一个点,相机点和消失点的连线与场景中的直线平行
X t = [ x 0 + t d 1 y 0 + t d 2 z 0 + t d 3 1 ] = [ x 0 / t + d 1 y 0 / t + d 2 z 0 / t + d 3 1 / t ] X_t=\begin{bmatrix} x_0+td_1\\y_0+td_2\\z_0+td_3 \\1 \end{bmatrix}=\begin{bmatrix} x_0/t+d_1\\y_0/t+d_2\\z_0/t+d_3 \\1/t \end{bmatrix} X t = ⎣ ⎢ ⎢ ⎡ x 0 + t d 1 y 0 + t d 2 z 0 + t d 3 1 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ x 0 / t + d 1 y 0 / t + d 2 z 0 / t + d 3 1 / t ⎦ ⎥ ⎥ ⎤
X ∞ = [ d 1 d 2 d 3 0 ] X_{\infty}=\begin{bmatrix} d_1\\d_2\\d_3\\0 \end{bmatrix} X ∞ = ⎣ ⎢ ⎢ ⎡ d 1 d 2 d 3 0 ⎦ ⎥ ⎥ ⎤
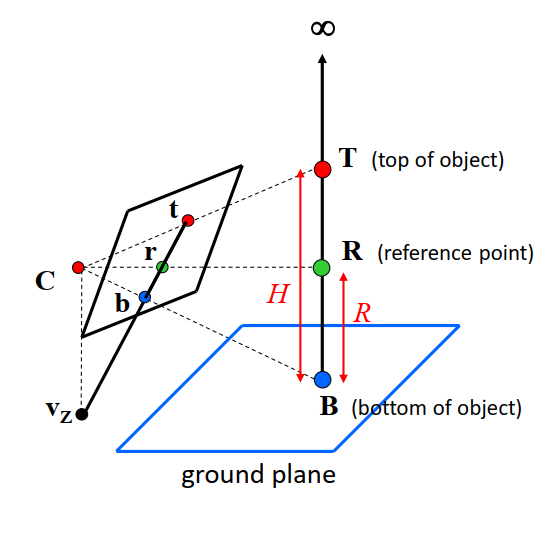
根据交比不变性,三维空间中:∣ ∣ T − B ∣ ∣ ∣ ∣ ∞ − R ∣ ∣ ∣ ∣ R − B ∣ ∣ ∣ ∣ ∞ − T ∣ ∣ = H R \frac{||T-B||||\infty-R||}{||R-B||||\infty-T||}=\frac{H}{R} ∣ ∣ R − B ∣ ∣ ∣ ∣ ∞ − T ∣ ∣ ∣ ∣ T − B ∣ ∣ ∣ ∣ ∞ − R ∣ ∣ = R H
在投影平面上:∣ ∣ t − b ∣ ∣ ∣ ∣ v z − r ∣ ∣ ∣ ∣ r − b ∣ ∣ ∣ ∣ v z − t ∣ ∣ = H R \frac{||t-b||||v_z-r||}{||r-b||||v_z-t||}=\frac{H}{R} ∣ ∣ r − b ∣ ∣ ∣ ∣ v z − t ∣ ∣ ∣ ∣ t − b ∣ ∣ ∣ ∣ v z − r ∣ ∣ = R H
图像中特征的查找在姿态估计和环境感知具有重要作用,在两张不同视角的图像中,找到相同的特征点,根据图像点的坐标变换,以及相机姿态变换或者改坐标实际三维坐标,就可以退出对应的信息。
但图像的特征提取受光照、噪声、能够检测的特征点个数所影响
定义
在其他含有相同场景或目标的相似图像中以一种相同的或至少非常相似的不变形式表示图像或目标。具有尺度不变性。
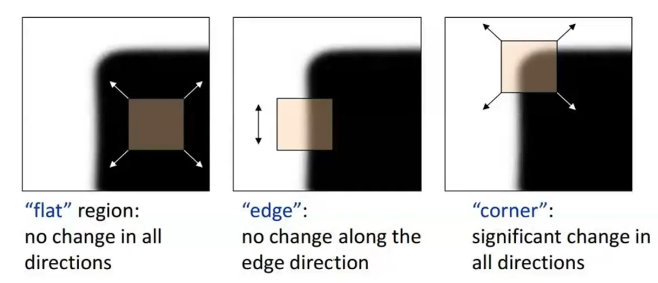
角点作为特征点最具代表性,在两个方向上都具有强烈变化。边缘和区块相对难以区分。
特征
可重复性(Repeatability):相同区域可以在不同的图像中被找到
可区别性(Distinctiveness):不同区域有不同的表达
高效性(Efficiency):同一图像中,特征点的数量应远小于像素的数量
局部性(Locality):特征仅与一小片图像区域有关
组成
关键点(Key Point);位置、大小、方向、评分等
描述子(Descriptor):特征点周围的图像信息,对旋转、平移、噪声等干扰具有抵抗能力
SIFT/SURF/ORB/BRIEF/BRISK
在(x,y)这个点统计x,y的变化率,得到变换方向[u,v]和Harris矩阵,再根据SVD分解,可以得到两个特征值,得到在两个方向的变化情况。若两个特征点都变化较大,则为角点
E ( u , v ) = ∑ x , y [ I ( x + u , y + v ) − I ( x , y ) ] 2 ≈ ∑ x , y w ( x , y ) [ I ( x , y ) + ∂ I ∂ x ( x , y ) u + ∂ I ∂ y ( x , y ) v − I ( x , y ) ] 2 = [ u v ] T H [ u v ] E(u,v)=\sum_{x,y}[I(x+u,y+v)-I(x,y)]^2\approx\sum_{x,y}w(x,y)[I(x,y)+\frac{\partial I}{\partial x}(x,y)u+\frac{\partial I}{\partial y}(x,y)v-I(x,y)]^2=\begin{bmatrix}u\\v\end{bmatrix}^TH\begin{bmatrix}u\\v\end{bmatrix} E ( u , v ) = ∑ x , y [ I ( x + u , y + v ) − I ( x , y ) ] 2 ≈ ∑ x , y w ( x , y ) [ I ( x , y ) + ∂ x ∂ I ( x , y ) u + ∂ y ∂ I ( x , y ) v − I ( x , y ) ] 2 = [ u v ] T H [ u v ]
图像梯度:△ I ( x , y ) = ( ∂ I ∂ x ( x , y ) , ∂ I ∂ y ( x , y ) ) \triangle I(x,y)=(\frac{\partial I}{\partial x}(x,y),\frac{\partial I}{\partial y}(x,y)) △ I ( x , y ) = ( ∂ x ∂ I ( x , y ) , ∂ y ∂ I ( x , y ) )
Harris矩阵:H = [ ∑ x , y w ( x , y ) ( ∂ I ∂ x ( x , y ) ) 2 ∑ x , y w ( x , y ) ( ∂ I ∂ x ( x , y ) ∂ I ∂ y ( x , y ) ) s u m x , y w ( x , y ) ( ∂ I ∂ x ( x , y ) ∂ I ∂ y ( x , y ) ) ∑ x , y w ( x , y ) ( ∂ I ∂ y ( x , y ) ) 2 ] H=\begin{bmatrix}\sum_{x,y}w(x,y)(\frac{\partial I}{\partial x}(x,y))^2&\sum_{x,y}w(x,y)(\frac{\partial I}{\partial x}(x,y)\frac{\partial I}{\partial y}(x,y))\\\\sum_{x,y}w(x,y)(\frac{\partial I}{\partial x}(x,y)\frac{\partial I}{\partial y}(x,y))&\sum_{x,y}w(x,y)(\frac{\partial I}{\partial y}(x,y))^2\end{bmatrix} H = ⎣ ⎡ ∑ x , y w ( x , y ) ( ∂ x ∂ I ( x , y ) ) 2 s u m x , y w ( x , y ) ( ∂ x ∂ I ( x , y ) ∂ y ∂ I ( x , y ) ) ∑ x , y w ( x , y ) ( ∂ x ∂ I ( x , y ) ∂ y ∂ I ( x , y ) ) ∑ x , y w ( x , y ) ( ∂ y ∂ I ( x , y ) ) 2 ⎦ ⎤
S V D ( H ) = U Σ V SVD(H)=U\Sigma V S V D ( H ) = U Σ V λ 1 , λ 2 \lambda_1,\lambda_2 λ 1 , λ 2
根据λ 1 , λ 2 \lambda_1,\lambda_2 λ 1 , λ 2
为了简化SVD求解,使用角点准则:C = d e t ( H ) − k t r a c e ( H ) 2 = λ 1 λ 2 − k ( λ 1 + λ 2 ) 2 C=det(H)-ktrace(H)^2=\lambda_1\lambda_2-k(\lambda_1+\lambda_2)^2 C = d e t ( H ) − k t r a c e ( H ) 2 = λ 1 λ 2 − k ( λ 1 + λ 2 ) 2
k越小,检测子越敏感
只有当λ 1 λ 2 \lambda_1\lambda_2 λ 1 λ 2
非极大值抑制(NMS),避免重复检测
缺点
尺度归一化的LoG算子
尺度空间:L ( x , y , σ ) L(x,y,\sigma) L ( x , y , σ )
步骤
尺度空间的极值检测:
尺度空间指一个变化尺度(σ)的二维高斯函数G(x,y,σ)与原图像I(x,y)卷积(即高斯模糊)后形成的空间,尺度不变特征应该既是空间域上又是尺度域上的局部极值。极值检测的大致原理是根据不同尺度下的高斯模糊化图像差异(Difference of Gaussians,DoG)寻找局部极值,这些找到的极值所对应的点被称为关键点或特征点。
关键点定位:
在不同尺寸空间下可能找出过多的关键点,有些关键点可能相对不易辨识或易受噪声干扰。该步借由关键点附近像素的信息、关键点的尺寸、关键点的主曲率来定位各个关键点,借此消除位于边上或是易受噪声干扰的关键点。
方向定位:
为了使描述符具有旋转不变性,需要利用图像的局部特征为给每一个关键点分配一个基准方向。通过计算关键点局部邻域的方向直方图,寻找直方图中最大值的方向作为关键点的主方向。
关键点描述子:
找到关键点的位置、尺寸并赋予关键点方向后,将可确保其移动、缩放、旋转的不变性。此外还需要为关键点建立一个描述子向量,使其在不同光线与视角下皆能保持其不变性。SIFT描述子是关键点邻域高斯图像梯度统计结果的一种表示,见下图。通过对关键点周围图像区域分块,计算块内梯度直方图,生成具有独特性的向量,这个向量是该区域图像信息的一种抽象,具有唯一性。Lowe在原论文中建议描述子使用在关键点尺度空间内44的窗口中计算的8个方向的梯度信息,共44*8=128维向量表征。(opencv中实现的也是128维)
(Speeded-Up Robust Features) 加速稳健特征
步骤
特征点检测:
SURF使用Hessian矩阵来检测特征点,该矩阵是x,y方向的二阶导数矩阵,可测量一个函数的局部曲率,其行列式值代表像素点周围的变化量,特征点需取行列式值的极值点。用方型滤波器取代SIFT中的高斯滤波器,利用积分图(计算位于滤波器方型的四个角落值)大幅提高运算速度。
特征点定位:
与SIFT类似,通过特征点邻近信息插补来定位特征点。
方向定位:
通过计算特征点周围像素点x,y方向的哈尔小波变换,并将x,y方向的变换值在xy平面某一角度区间内相加组成一个向量,在所有的向量当中最长的(即x、y分量最大的)即为此特征点的方向。
特征描述子:
选定了特征点的方向后,其周围相素点需要以此方向为基准来建立描述子。此时以55个像素点为一个子区域,取特征点周围2020个像素点的范围共16个子区域,计算子区域内的x、y方向(此时以平行特征点方向为x、垂直特征点方向为y)的哈尔小波转换总和Σdx、ΣdyΣdx、Σdy与其向量长度总和Σ|dx|、Σ|dy|Σ|dx|、Σ|dy|共四个量值,共可产生一个64维的描述子。
是一种角点检测,主要检测局部像素灰度变化明显的地方,以速度快著称
如果一个像素与它邻域的像素差别较大,则其更有可能是角点。
由于相机的旋转,相同的角点会有旋转变化,按照相同矩形框范围计算描述子会导致结果的不同
Oriented FAST在FAST基础上,计算旋转,得到的选择框可以与之前的检测更为相似,具体过程:
在一个细小的图像块B中,定义图像块的矩为:
m p q = ∑ x , y ∈ B x p y q I ( x , y ) , p , q = 0 , 1 m_{pq}=\sum_{x,y\in B}x^py^qI(x,y),\;p,q={0,1} m p q = ∑ x , y ∈ B x p y q I ( x , y ) , p , q = 0 , 1
通过矩可以找到图像块的质心:
C = ( m 10 m 00 , m 01 m 00 ) C=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}}) C = ( m 0 0 m 1 0 , m 0 0 m 0 1 )
链接图像块的几何中心O与质心C,得到一个方向向量O C → \overrightarrow{OC} O C
θ = a r c t a n ( m 01 m 10 ) \theta=arctan(\frac{m_{01}}{m_{10}}) θ = a r c t a n ( m 1 0 m 0 1 )
随机选点的方法
x i x_i x i y i y_i y i [ − S 2 , S 2 ] [-\frac{S}{2},\frac{S}{2}] [ − 2 S , 2 S ] x i x_i x i y i y_i y i [ 0 , 1 25 S 2 ] [0,\frac{1}{25}S^2] [ 0 , 2 5 1 S 2 ] x i x_i x i [ 0 , 1 25 S 2 ] [0,\frac{1}{25}S^2] [ 0 , 2 5 1 S 2 ] y i y_i y i [ x i , 1 100 S 2 ] [x_i,\frac{1}{100}S^2] [ x i , 1 0 0 1 S 2 ] x i x_i x i x i x_i x i y i y_i y i x i x_i x i y i y_i y i x i = ( 0 , 0 ) T x_i=(0,0)^T x i = ( 0 , 0 ) T y i y_i y i
作者实验证明第2种方法效果更好
关键点:Oriented FAST,计算了特征点的主要方向,增加了旋转不变性
描述子:BRIEF,对前一步的特征点周围图像区域进行描述
特征匹配:通过描述子的差异判断哪些特征为同一个点,ORB可以用汉明距离
暴力匹配:比较两图每个特征间的距离
得到特征点后,需要得到特征点之间的对应关系,得到相机的旋转和平移
如果只有两个单目图像:对极几何2D-2D
帧和地图:PnP,3D-2D
RGB-D图:ICP,3D-3D
Epipolar Geometry:不知道3D信息时,估计相机的运动(外参)
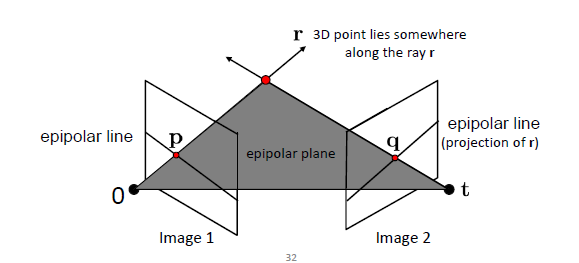
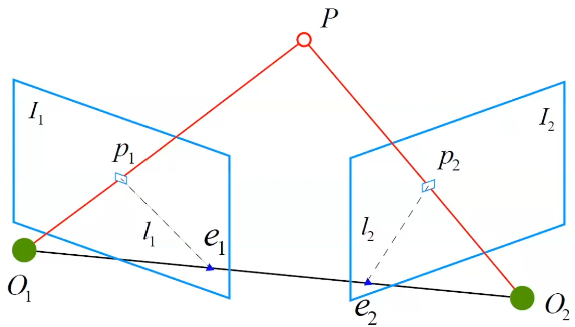
极点(epipoles):相机的远点,在另外一个相机的投影:e 1 e_1 e 1 e 2 e_2 e 2
极线(epipolar line):目标点到相机的连线:l 1 l_1 l 1 l 2 l_2 l 2
基线(baseline):O 1 O 2 O_1O_2 O 1 O 2
极平面(epipolar plane):O 1 O 2 P O_1O_2P O 1 O 2 P
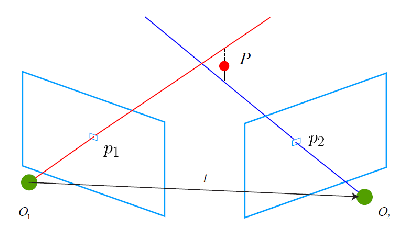
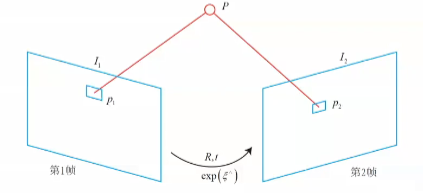
空间点的世界坐标为P ( X , Y , Z ) P(X,Y,Z) P ( X , Y , Z ) O 1 O_1 O 1 I 1 I_1 I 1 I 2 I_2 I 2 p 1 p_1 p 1 p 2 p_2 p 2 p 1 p_1 p 1 p 2 p_2 p 2
O 1 P O_1P O 1 P O 2 P O_2P O 2 P e 2 p 2 ( l 2 ) e_2p_2(l_2) e 2 p 2 ( l 2 ) e 1 p 1 ( l 1 ) e_1p_1(l_1) e 1 p 1 ( l 1 ) O 1 O 2 O_1O_2 O 1 O 2 e 1 e_1 e 1 e 2 e_2 e 2 根据p,q,一定可以恢复3维的坐标P,通过对极线和对极平面,在image1中的特征点,对应image2中,只需要查找对极线的位置就可以了,减小了搜索范围
相机O 1 O_1 O 1 T 12 ( R , t ) T_{12}(R,t) T 1 2 ( R , t ) O 2 O_2 O 2
以第一个O 1 O_1 O 1 s p sp s p
s 1 p 1 = K P s_1p_1=KP s 1 p 1 = K P s 2 p 2 = K ( R P + t ) s_2p_2=K(RP+t) s 2 p 2 = K ( R P + t )
利用归一化坐标的性质(齐次坐标),x乘以任意s都表示同一向量,将尺度s放进x里:
x 1 = K − 1 p 1 x_1=K^{-1}p_1 x 1 = K − 1 p 1 x 2 = K − 1 p 2 x_2=K^{-1}p_2 x 2 = K − 1 p 2 可以得到齐次关系:x 2 = R x 1 + t x_2=Rx_1+t x 2 = R x 1 + t
等式两边同乘x 2 T t ∧ x_2^Tt^\wedge x 2 T t ∧
x 2 T t ∧ x 2 = x 2 T t ∧ R x 1 + x 2 T t ∧ t x_2^Tt^\wedge x_2=x_2^Tt^\wedge Rx_1+x_2^Tt^\wedge t x 2 T t ∧ x 2 = x 2 T t ∧ R x 1 + x 2 T t ∧ t
t ∧ t t^\wedge t t ∧ t x 2 T t ∧ x 2 x_2^Tt^\wedge x_2 x 2 T t ∧ x 2 t ∧ x 2 t^\wedge x_2 t ∧ x 2 x 2 T x_2^T x 2 T
得到对极约束:
x 2 T t ∧ R x 1 = 0 x_2^Tt^\wedge Rx_1=0 x 2 T t ∧ R x 1 = 0
带内参形式的对极约束:
p 2 T K − 1 t ∧ R K − 1 p 1 p_2^TK^{-1}t^\wedge RK^{-1}p_1 p 2 T K − 1 t ∧ R K − 1 p 1
对极约束的意义是O 1 O 2 P O_1O_2P O 1 O 2 P
定义E = t ∧ R E=t\wedge R E = t ∧ R F = K − 1 E K − 1 F=K^{-1}EK^{-1} F = K − 1 E K − 1
由于尺度放在x中,实际对于任意λ \lambda λ λ x \lambda x λ x
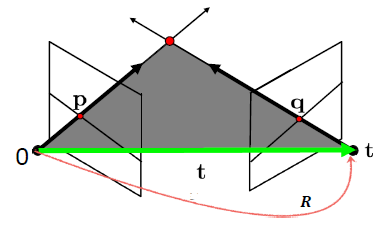
两个相机的位置,可以用R|t表示,已知p和q,根据向量的混合积公式,由于op、ot和tq共线,他们的混合积为零:p ⋅ ( t × R T q ) = 0 p\cdot(t\times R^Tq)=0 p ⋅ ( t × R T q ) = 0 R T q R^Tq R T q
叉乘可以转化为:
[ a ] × = [ 0 − a z a y a z 0 − a x − a y a x 0 ] [a]_\times=\begin{bmatrix} 0&-a_z&a_y\\a_z&0&-a_x\\-a_y&a_x&0 \end{bmatrix} [ a ] × = ⎣ ⎡ 0 a z − a y − a z 0 a x a y − a x 0 ⎦ ⎤ p ⋅ ( t × R T q ) = p T [ t ] × R T q = q T R [ t ] × p = q T E p = 0 p\cdot(t\times R^Tq)=p^T[t]_\times R^Tq=q^TR[t]_\times p=q^TEp=0 p ⋅ ( t × R T q ) = p T [ t ] × R T q = q T R [ t ] × p = q T E p = 0
E = R [ t ] × E=R[t]_\times E = R [ t ] ×
本质矩阵:E = t ∧ R E=t\wedge R E = t ∧ R
两对点x 1 = [ u 1 , v 1 , 1 ] T x_1=[u_1,v_1,1]^T x 1 = [ u 1 , v 1 , 1 ] T x 2 = [ u 2 , v 2 , 1 ] T x_2=[u_2,v_2,1]^T x 2 = [ u 2 , v 2 , 1 ] T
根据对极约束:
[ u 1 v 1 1 ] ⋅ E ⋅ [ u 2 v 2 1 ] = 0 \begin{bmatrix}u_1&v_1&1\end{bmatrix}\cdot E\cdot\begin{bmatrix}u_2&v_2&1\end{bmatrix}=0 [ u 1 v 1 1 ] ⋅ E ⋅ [ u 2 v 2 1 ] = 0 其中E = [ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ] E=\begin{bmatrix}e_1&e_2&e_3\\e_4&e_5&e_6\\e_7&e_8&e_9\\\end{bmatrix} E = ⎣ ⎡ e 1 e 4 e 7 e 2 e 5 e 8 e 3 e 6 e 9 ⎦ ⎤
把约束向量化:
[ u 1 u 2 u 1 v 2 u 1 v 1 u 2 v 1 v 2 v 1 u 2 v 2 1 ] [ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ] = 0 \begin{bmatrix}u_1u_2&u_1v_2&u_1&v_1u_2&v_1v_2&v_1&u_2&v_2&1\end{bmatrix}\begin{bmatrix}e_1\\e_2\\e_3\\e_4\\e_5\\e_6\\e_7\\e_8\\e_9\end{bmatrix}=0 [ u 1 u 2 u 1 v 2 u 1 v 1 u 2 v 1 v 2 v 1 u 2 v 2 1 ] ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = 0 [ u 1 1 u 2 1 u 1 1 v 2 1 u 1 1 v 1 1 u 2 1 v 1 1 v 2 1 v 1 1 u 2 1 v 2 1 1 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ u 1 8 u 2 8 u 1 8 v 2 8 u 1 8 v 1 8 u 2 8 v 1 8 v 2 8 v 1 8 u 2 8 v 2 8 1 ] [ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ] = 0 \begin{bmatrix}u_1^1u_2^1&u_1^1v_2^1&u_1^1&v_1^1u_2^1&v_1^1v_2^1&v_1^1&u_2^1&v_2^1&1\\\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\u_1^8u_2^8&u_1^8v_2^8&u_1^8&v_1^8u_2^8&v_1^8v_2^8&v_1^8&u_2^8&v_2^8&1\end{bmatrix}\begin{bmatrix}e_1\\e_2\\e_3\\e_4\\e_5\\e_6\\e_7\\e_8\\e_9\end{bmatrix}=0 ⎣ ⎢ ⎡ u 1 1 u 2 1 ⋮ u 1 8 u 2 8 u 1 1 v 2 1 ⋮ u 1 8 v 2 8 u 1 1 ⋮ u 1 8 v 1 1 u 2 1 ⋮ v 1 8 u 2 8 v 1 1 v 2 1 ⋮ v 1 8 v 2 8 v 1 1 ⋮ v 1 8 u 2 1 ⋮ u 2 8 v 2 1 ⋮ v 2 8 1 ⋮ 1 ⎦ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = 0
将8对点组合成为线性方程组,进行奇异值分解:
E = U Λ V T E=U\Lambda V^T E = U Λ V T 四个可能解:
t 1 ∧ = U R Z ( π 2 Λ U T ) t_1^\wedge=UR_Z(\frac{\pi}{2}\Lambda U^T) t 1 ∧ = U R Z ( 2 π Λ U T ) t 2 ∧ = U R Z ( − π 2 Λ U T ) t_2^\wedge=UR_Z(-\frac{\pi}{2}\Lambda U^T) t 2 ∧ = U R Z ( − 2 π Λ U T ) R 1 = U R Z T ( π 2 Λ V T ) R_1=UR_Z^T(\frac{\pi}{2}\Lambda V^T) R 1 = U R Z T ( 2 π Λ V T ) R 2 = U R Z T ( π 2 Λ V T ) R_2=UR_Z^T(\frac{\pi}{2}\Lambda V^T) R 2 = U R Z T ( 2 π Λ V T )
图一深度都是正的,其余深度不全为正
8点法求得的E具有8个自由度,需要反推变换矩阵时还需要满足内在性质要求,奇异值为:[ δ , δ , 0 ] [\delta,\delta,0] [ δ , δ , 0 ]
在SVD过程中取:E = U d i a g ( δ 1 + δ 2 2 , δ 1 + δ 2 2 , 0 ) V T E=U diag(\frac{\delta_1+\delta_2}{2},\frac{\delta_1+\delta_2}{2},0)V^T E = U d i a g ( 2 δ 1 + δ 2 , 2 δ 1 + δ 2 , 0 ) V T
八点法
用于单目SLAM初始化
尺度不确定性:无法知道尺度,一般方法归一化t或特征特点的平均深度
由于E = t ∧ R E=t\wedge R E = t ∧ R
多于8对点时,可以使用最小二乘法确定E
有外点时:RANSAC
特征点共面的时候,E会退化,这就可以用单应矩阵解决
作用:将image1上的点映射到image2中
当已知相机内参K时:相机像素坐标系可以转化为世界坐标系:y = K − 1 x y=K^{-1}x y = K − 1 x
根据p = K 1 − 1 p ^ p=K^{-1}_1\hat p p = K 1 − 1 p ^ q = K 2 − 1 q ^ q=K^{-1}_2\hat q q = K 2 − 1 q ^ q T E p = 0 q^TEp=0 q T E p = 0 p ^ q ^ \hat p\hat q p ^ q ^
可以得到:q ^ T K 2 − 1 E K 1 − 1 p ^ = q ^ T ( K 2 − 1 E K 1 − 1 ) p ^ = q ^ T F p ^ = 0 \hat q^TK^{-1}_2EK^{-1}_1\hat p=\hat q^T(K^{-1}_2EK^{-1}_1)\hat p=\hat q^TF\hat p=0 q ^ T K 2 − 1 E K 1 − 1 p ^ = q ^ T ( K 2 − 1 E K 1 − 1 ) p ^ = q ^ T F p ^ = 0
F就是3x3的Fundamental matrix
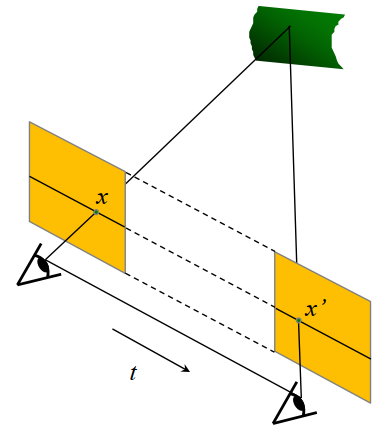
如果使两个相机高度相同,焦距相同,成像的平面也是平行的,此时两个对极线会在图像的同一高度上
x ′ T E x = 0 x^{\prime T}Ex=0 x ′ T E x = 0 E = [ t ] × R E=[t]_\times R E = [ t ] × R R = I R=I R = I t = ( T , 0 , 0 ) t=(T,0,0) t = ( T , 0 , 0 )
E = [ t ] × R = [ 0 0 0 0 0 − T 0 T 0 ] E=[t]_\times R=\begin{bmatrix} 0&0&0\\0&0&-T\\0&T&0\end{bmatrix} E = [ t ] × R = ⎣ ⎡ 0 0 0 0 0 T 0 − T 0 ⎦ ⎤
可得:T v ′ = T v Tv^\prime=Tv T v ′ = T v
对于非标准的相机,可以矫正为标准的
已知Baseline:B,x和x’坐标,焦距都为f,可以通过相似三角形得到深度
x − x ′ f = B z \frac{x-x\prime}{f}=\frac{B}{z} f x − x ′ = z B d i s p a r i t y = x − x ′ = B ⋅ f z disparity=x-x^\prime=\frac{B\cdot f}{z} d i s p a r i t y = x − x ′ = z B ⋅ f z = B ⋅ f x − x ′ z=\frac{B\cdot f}{x-x^\prime} z = x − x ′ B ⋅ f
已知空间一点的齐次化坐标P ( X , Y , Z , 1 ) T P(X,Y,Z,1)^T P ( X , Y , Z , 1 ) T x 1 = ( u 1 , v 1 , 1 ) T x_1=(u_1,v_1,1)^T x 1 = ( u 1 , v 1 , 1 ) T
投影关系:
s x = R ⋅ p + t = [ R , t ] P sx=R\cdot p+t=[R,t]P s x = R ⋅ p + t = [ R , t ] P s [ u 1 v 1 1 ] = [ t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 10 t 11 t 12 ] [ X Y Z 1 ] s\begin{bmatrix}u_1\\v_1\\1\end{bmatrix}=\begin{bmatrix}t_1&t_2&t_3&t_4\\t_5&t_6&t_7&t_8\\t_9&t_{10}&t_{11}&t_{12}\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix} s ⎣ ⎡ u 1 v 1 1 ⎦ ⎤ = ⎣ ⎡ t 1 t 5 t 9 t 2 t 6 t 1 0 t 3 t 7 t 1 1 t 4 t 8 t 1 2 ⎦ ⎤ ⎣ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎤
最后一行求得s,用于消去前两行的s:
s = [ t 9 , t 10 , t 11 , t 12 ] [ X , Y , Z , 1 ] T s=[t_9,t_{10},t_{11},t_{12}][X,Y,Z,1]^T s = [ t 9 , t 1 0 , t 1 1 , t 1 2 ] [ X , Y , Z , 1 ] T
求得u1,v1:
u 1 = t 1 X + t 2 Y + t 3 Z + t 4 t 9 X + t 10 Y + t 11 Z + t 12 u_1=\frac{t_1X+t_2Y+t_3Z+t_4}{t_9X+t_{10}Y+t_{11}Z+t_{12}} u 1 = t 9 X + t 1 0 Y + t 1 1 Z + t 1 2 t 1 X + t 2 Y + t 3 Z + t 4 v 1 = t 5 X + t 6 Y + t 7 Z + t 8 t 9 X + t 10 Y + t 11 Z + t 12 v_1=\frac{t_5X+t_6Y+t_7Z+t_8}{t_9X+t_{10}Y+t_{11}Z+t_{12}} v 1 = t 9 X + t 1 0 Y + t 1 1 Z + t 1 2 t 5 X + t 6 Y + t 7 Z + t 8
为了简化,定义:
t 1 = ( t 1 , t 2 , t 3 , t 4 ) T t_1=(t_1,t_2,t_3,t_4)^T t 1 = ( t 1 , t 2 , t 3 , t 4 ) T t 2 = ( t 5 , t 6 , t 7 , t 8 ) T t_2=(t_5,t_6,t_7,t_8)^T t 2 = ( t 5 , t 6 , t 7 , t 8 ) T t 3 = ( t 9 , t 10 , t 11 , t 12 ) T t_3=(t_9,t_{10},t_{11},t_{12})^T t 3 = ( t 9 , t 1 0 , t 1 1 , t 1 2 ) T
则一个特征点提供两个方程:
t 1 T P − t 3 T u 1 = 0 t_1^TP-t_3^Tu_1=0 t 1 T P − t 3 T u 1 = 0 t 2 T P − t 3 T v 1 = 0 t_2^TP-t_3^Tv_1=0 t 2 T P − t 3 T v 1 = 0
向量化:
[ P 1 T 0 − u 1 P 1 T 0 P 1 T − v 1 P 1 T ⋮ P N T 0 − u 1 P N T 0 P N T − v 1 P N T ] [ t 1 t 2 t 3 ] = 0 \begin{bmatrix}P_1^T&0&-u_1P_1^T\\0&P_1^T&-v_1P_1^T\\&\vdots&\\P_N^T&0&-u_1P_N^T\\0&P_N^T&-v_1P_N^T\end{bmatrix}\begin{bmatrix}t_1\\t_2\\t_3\end{bmatrix}=0 ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ P 1 T 0 P N T 0 0 P 1 T ⋮ 0 P N T − u 1 P 1 T − v 1 P 1 T − u 1 P N T − v 1 P N T ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎡ t 1 t 2 t 3 ⎦ ⎤ = 0
其中可以直接求出t = [ t 4 , t 8 , t 1 2 ] t=[t_4,t_8,t_12] t = [ t 4 , t 8 , t 1 2 ] [ R ∣ t ] [R|t] [ R ∣ t ]
理论上使用6对点就可以求得结果,超定时求最小二乘解。这种方法叫做直接线型变换。
通常在噪声的情况下,矩阵的秩、特征值、线性关系等并不能很好的保持,一般使用优化方法:BA
最小化重投影误差(minimize the Reprojection Error)
已知在o1坐标系下的N个空间点P ( X i , Y i , Z i , 1 ) T P(X_i,Y_i,Z_i,1)^T P ( X i , Y i , Z i , 1 ) T u i = ( u 1 , v i ) T u_i=(u_1,v_i)^T u i = ( u 1 , v i ) T ξ \xi ξ
投影关系(齐次坐标):
s i u i = K e x p ( ξ ∧ ) P i s_iu_i=Kexp(\xi^\wedge)P_i s i u i = K e x p ( ξ ∧ ) P i
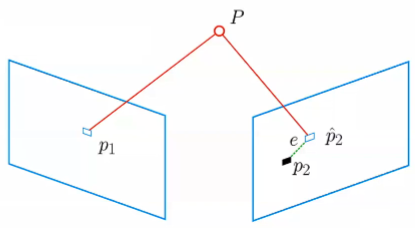
现实世界存在误差,p 1 p_1 p 1 p ^ 2 \hat{p}_2 p ^ 2 p 2 p_2 p 2
求取ξ \xi ξ ξ ∗ \xi^* ξ ∗
ξ ∗ = arg min ξ 1 2 ∑ i = 1 n ∥ u i − 1 s i K e x p ( ξ ∧ ) P i ∥ 2 2 \xi^*=\arg\min_{\xi}\frac{1}{2}\sum_{i=1}^{n}\left\|u_i-\frac{1}{s_i}Kexp(\xi^\wedge)P_i\right\|_2^2 ξ ∗ = arg min ξ 2 1 ∑ i = 1 n ∥ ∥ ∥ u i − s i 1 K e x p ( ξ ∧ ) P i ∥ ∥ ∥ 2 2
求解最小化的方法就是使用非线性最小二乘的方法,求解雅克比矩阵J T J △ x = − J T e J^TJ\triangle x=-J^Te J T J △ x = − J T e
e i = u i − 1 s i K e x p ( ξ ∧ ) P i e_i=u_i-\frac{1}{s_i}Kexp(\xi^\wedge)P_i e i = u i − s i 1 K e x p ( ξ ∧ ) P i 其一阶泰勒展开。线性化:
e i ( x + △ x ) ≈ e i ( x ) + J ( x ) △ x e_i(x+\triangle x)\approx e_i(x)+J(x)\triangle x e i ( x + △ x ) ≈ e i ( x ) + J ( x ) △ x
使用李代数形式求解雅克比形式:
∂ e ∂ δ ξ = lim δ ξ → 0 e ( δ ξ ⊕ ξ ) δ ξ = ∂ e ∂ P ′ ∂ P ′ ∂ δ ξ \frac{\partial e}{\partial\delta\xi}=\lim_{\delta\xi\rightarrow0}\frac{e(\delta\xi\oplus\xi)}{\delta\xi}=\frac{\partial e}{\partial P'}\frac{\partial P'}{\partial \delta \xi} ∂ δ ξ ∂ e = lim δ ξ → 0 δ ξ e ( δ ξ ⊕ ξ ) = ∂ P ′ ∂ e ∂ δ ξ ∂ P ′ 其中⊕ \oplus ⊕
P’为P在相机坐标系下的坐标P ′ = ( e x p ( ξ ∧ ) P ) 1 : 3 = [ X ′ , Y ′ , Z ′ ] T P'=(exp(\xi^\wedge)P)_{1:3}=[X',Y',Z']^T P ′ = ( e x p ( ξ ∧ ) P ) 1 : 3 = [ X ′ , Y ′ , Z ′ ] T
对P’进行投影,求P’投影的内参矩阵表示:
s u = K P ′ = [ s u s v s ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X ′ Y ′ Z ′ ] su=KP'=\begin{bmatrix}su\\sv\\s\end{bmatrix}=\begin{bmatrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}\begin{bmatrix}X'\\Y'\\Z'\end{bmatrix} s u = K P ′ = ⎣ ⎡ s u s v s ⎦ ⎤ = ⎣ ⎡ f x 0 0 0 f y 0 c x c y 1 ⎦ ⎤ ⎣ ⎡ X ′ Y ′ Z ′ ⎦ ⎤
(u,v)的公式
{ u = f x X ′ Z ′ + c x v = f y Y ′ Z ′ + c y \begin{cases}u=f_x\frac{X'}{Z'}+c_x\\v=f_y\frac{Y'}{Z'}+c_y\end{cases} { u = f x Z ′ X ′ + c x v = f y Z ′ Y ′ + c y
根据链式法则,可得第一项的求导:
∂ e ∂ P ′ = − [ ∂ u ∂ X ′ ∂ u ∂ Y ′ ∂ u ∂ Z ′ ∂ v ∂ X ′ ∂ v ∂ Y ′ ∂ v ∂ Z ′ ] = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] \frac{\partial e}{\partial P'}=-\begin{bmatrix}\frac{\partial u}{\partial X'}&\frac{\partial u}{\partial Y'}&\frac{\partial u}{\partial Z'}\\\frac{\partial v}{\partial X'}&\frac{\partial v}{\partial Y'}&\frac{\partial v}{\partial Z'}\end{bmatrix}=-\begin{bmatrix}\frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}\end{bmatrix} ∂ P ′ ∂ e = − [ ∂ X ′ ∂ u ∂ X ′ ∂ v ∂ Y ′ ∂ u ∂ Y ′ ∂ v ∂ Z ′ ∂ u ∂ Z ′ ∂ v ] = − [ Z ′ f x 0 0 Z ′ f y − Z ′ 2 f x X ′ − Z ′ 2 f y Y ′ ]
第二项的求解:
∂ ( T P ) ∂ δ ξ = ( T P ) ⊙ = [ I − P ′ ∧ 0 T 0 T ] \frac{\partial(TP)}{\partial\delta\xi}=(TP)^\odot=\begin{bmatrix}I&-P'^\wedge\\0^T&0^T\end{bmatrix} ∂ δ ξ ∂ ( T P ) = ( T P ) ⊙ = [ I 0 T − P ′ ∧ 0 T ] 非齐次形式:∂ P ′ ∂ δ ξ = [ I − P ′ ∧ ] \frac{\partial P'}{\partial\delta\xi}=[I\; -{P'}^\wedge] ∂ δ ξ ∂ P ′ = [ I − P ′ ∧ ]
两项相乘,总的求导结果为:
∂ e ∂ δ ξ = − [ f x Z ′ 0 − f x X ′ Z ′ 2 − f x X ′ Y ′ Z ′ 2 f x + f x X 2 Z ′ 2 − f x Y ′ Z ′ 0 f y Z ′ − f y Y ′ Z ′ 2 − f y − f y Y 2 Z ′ 2 f y X ′ Y ′ Z ′ 2 f y X ′ Z ′ ] \frac{\partial e}{\partial\delta\xi}=-\begin{bmatrix}\frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}&-\frac{f_xX'Y'}{Z'^2}&f_x+\frac{f_xX^2}{Z'^2}&-\frac{f_xY'}{Z'}\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}&-f_y-\frac{f_yY^2}{Z'^2}&\frac{f_yX'Y'}{Z'^2}&\frac{f_yX'}{Z'}\end{bmatrix} ∂ δ ξ ∂ e = − [ Z ′ f x 0 0 Z ′ f y − Z ′ 2 f x X ′ − Z ′ 2 f y Y ′ − Z ′ 2 f x X ′ Y ′ − f y − Z ′ 2 f y Y 2 f x + Z ′ 2 f x X 2 Z ′ 2 f y X ′ Y ′ − Z ′ f x Y ′ Z ′ f y X ′ ]
以此为J,用于计算增量迭代更新
∑ J T J △ x = − ∑ J T e \sum J^TJ\triangle x=-\sum J^Te ∑ J T J △ x = − ∑ J T e 其中△ x = δ ξ \triangle x=\delta\xi △ x = δ ξ
更新:T ← e x p ( δ ξ ∧ ) ⋅ T T\leftarrow exp(\delta\xi^\wedge)\cdot T T ← e x p ( δ ξ ∧ ) ⋅ T
也可以对3D点求导:
e i = u i − 1 s i K e x p ( ξ ∧ ) P i e_i=u_i-\frac{1}{s_i}Kexp(\xi^\wedge)P_i e i = u i − s i 1 K e x p ( ξ ∧ ) P i ∂ e ∂ P = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] R \frac{\partial e}{\partial P}=-\begin{bmatrix}\frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}\end{bmatrix}R ∂ P ∂ e = − [ Z ′ f x 0 0 Z ′ f y − Z ′ 2 f x X ′ − Z ′ 2 f y Y ′ ] R
迭代最临界点(Iterative Closest Point):给定配对好的两组3D点,估计相机的旋转和平移运动(外参)
两个点
P = [ p 1 , … , p n ] P=[p_1,\dots,p_n] P = [ p 1 , … , p n ] P ′ = [ p 1 ′ , … , p n ′ ] P'=[p_1',\dots,p_n'] P ′ = [ p 1 ′ , … , p n ′ ]
运动关系
∀ i , p i = R p i ′ + t \forall i,p_i=Rp_i' +t ∀ i , p i = R p i ′ + t
误差项
e i = p i − ( R p i ′ + t ) e_i=p_i-(Rp_i'+t) e i = p i − ( R p i ′ + t )
最小二乘问题:
min R , t J = 1 2 ∑ i = 1 n ∥ p i − ( R p i ′ + t ) ∥ 2 2 \min{R,t}J=\frac{1}{2}\sum_{i=1}^{n}\left\|p_i-(Rp_i'+t)\right\|_2^2 min R , t J = 2 1 ∑ i = 1 n ∥ p i − ( R p i ′ + t ) ∥ 2 2
计算质心并定义质心p和p’,根据质心位置可以用于空间点的平移:
p = 1 n ∑ i = 1 n ( p i ) p=\frac{1}{n}\sum_{i=1}^{n}(p_i) p = n 1 ∑ i = 1 n ( p i ) p ′ = 1 n ∑ i = 1 n ( p i ′ ) p'=\frac{1}{n}\sum_{i=1}^{n}(p_i') p ′ = n 1 ∑ i = 1 n ( p i ′ )
去除质心后的目标函数
1 2 ∑ i = 1 n ∥ p i − ( R p i ′ + t ) ∥ 2 = 1 2 ∑ i = 1 n ∥ p i − R p i ′ − t − p + p − R p ′ + R p ′ ∥ 2 = 1 2 ∑ i = 1 n ∥ ( p i − p − R ( p i ′ − p ′ ) ) + ( p − R p ′ − t ) ∥ 2 = 1 2 ∑ i = 1 n ∥ p i − p − R ( p i ′ − p ′ ) ∥ 2 + ∥ p − R p ′ − t ∥ 2 + 2 ( p i − p − R ( p i ′ − p ′ ) ) T ( p − R p ′ − t ) \frac{1}{2}\sum_{i=1}^{n}\left\|p_i-(Rp_i'+t)\right\|^2=\frac{1}{2}\sum_{i=1}^{n}\left\|p_i-Rp_i'-t-p+p-Rp'+Rp'\right\|^2=\frac{1}{2}\sum_{i=1}^{n}\left\|(p_i-p-R(p_i'-p'))+(p-Rp'-t)\right\|^2=\frac{1}{2}\sum_{i=1}^{n}\left\|p_i-p-R(p_i'-p')\right\|^2+\left\|p-Rp'-t\right\|^2+2(p_i-p-R(p_i'-p'))^T(p-Rp'-t) 2 1 ∑ i = 1 n ∥ p i − ( R p i ′ + t ) ∥ 2 = 2 1 ∑ i = 1 n ∥ p i − R p i ′ − t − p + p − R p ′ + R p ′ ∥ 2 = 2 1 ∑ i = 1 n ∥ ( p i − p − R ( p i ′ − p ′ ) ) + ( p − R p ′ − t ) ∥ 2 = 2 1 ∑ i = 1 n ∥ p i − p − R ( p i ′ − p ′ ) ∥ 2 + ∥ p − R p ′ − t ∥ 2 + 2 ( p i − p − R ( p i ′ − p ′ ) ) T ( p − R p ′ − t )
由于交叉项部分求和为零( p i − p − R ( p i ′ − p ′ ) ) T ( p − R p ′ − t ) = 0 (p_i-p-R(p_i'-p'))^T(p-Rp'-t)=0 ( p i − p − R ( p i ′ − p ′ ) ) T ( p − R p ′ − t ) = 0
min R , t J = 1 2 ∑ i = 1 n ∥ p i − p − R ( p i ′ − p ′ ) ∥ 2 + ∥ p − R p ′ − t ∥ 2 \min{R,t}J=\frac{1}{2}\sum_{i=1}^{n}\left\|p_i-p-R(p_i'-p')\right\|^2+\left\|p-Rp'-t\right\|^2 min R , t J = 2 1 ∑ i = 1 n ∥ p i − p − R ( p i ′ − p ′ ) ∥ 2 + ∥ p − R p ′ − t ∥ 2
ICP求解过程
计算两组点的质心的位置p、p’,然后计算每个点的去质心坐标
q i = p i − p q_i=p_i-p q i = p i − p q i ′ = p i ′ − p ′ q_i'=p_i'-p' q i ′ = p i ′ − p ′
根据优化问题,得到旋转矩阵R:
R ∗ = arg min R 1 2 ∑ i = 1 n ∥ q i − R q i ′ ∥ 2 = 1 2 ∑ i = 1 n q i T q i + q i ′ T R ′ R q i ′ − 2 q i T R q i ′ R^*=\arg\min_{R}\frac{1}{2}\sum_{i=1}^{n}\left\|q_i-Rq_i'\right\|^2=\frac{1}{2}\sum_{i=1}^{n}q_i^Tq_i+{q_i}'^TR'Rq_i'-2q_i^TRq_i' R ∗ = arg min R 2 1 ∑ i = 1 n ∥ q i − R q i ′ ∥ 2 = 2 1 ∑ i = 1 n q i T q i + q i ′ T R ′ R q i ′ − 2 q i T R q i ′
其中第一项与R无关,第二项R ′ R = I R'R=I R ′ R = I
∑ i = 1 n − q i T R q i ′ = ∑ i = 1 n − t r ( R q i ′ q i T ) = − t r ( R ∑ i = 1 n q i ′ q i T ) \sum_{i=1}^{n}-q_i^TRq_i'=\sum_{i=1}^{n}-tr(Rq_i'q_i^T)=-tr(R\sum_{i=1}^{n}q_i'q_i^T) ∑ i = 1 n − q i T R q i ′ = ∑ i = 1 n − t r ( R q i ′ q i T ) = − t r ( R ∑ i = 1 n q i ′ q i T )
通过SVD求解R:设W = ∑ i = 1 n q i ′ q i T ) W=\sum_{i=1}^{n}q_i'q_i^T) W = ∑ i = 1 n q i ′ q i T )
W = U Σ V T W=U\Sigma V^T W = U Σ V T R = U V T R=UV^T R = U V T
得到t:t ∗ = p − R p ′ t^*=p-Rp' t ∗ = p − R p ′
当两组P对应关系呈非线性分布时,SVD有解析解,是可以确定唯一的R和t
在两组点都在一条直线上,会遇到退化问题,可能有无穷多解
激光环境下,匹配点位置,将指定最近点为匹配点,此时问题非凸极小值不一定为最小值。
利用非线性优化可以将ICP与PnP结合一起求解
e = e 3 D − 3 D + e 3 D − 2 D e=e_{3D-3D}+e_{3D-2D} e = e 3 D − 3 D + e 3 D − 2 D
当已知相机运动,求解特征点P的3D位置
几何关系:
s 1 x 1 = s 2 R x 2 + t s_1x_1=s_2Rx_2+t s 1 x 1 = s 2 R x 2 + t 其中x1,x2为归一化坐标
求解s 2 s_2 s 2 x 1 ∧ x_1^\wedge x 1 ∧ s 1 x 1 ∧ x 1 = 0 s_1x_1^\wedge x_1=0 s 1 x 1 ∧ x 1 = 0
s 2 x 1 ∧ R x 2 + x 1 ∧ t s_2x_1^\wedge Rx_2+x_1^\wedge t s 2 x 1 ∧ R x 2 + x 1 ∧ t 求解s 1 s_1 s 1
或者同时解s 1 , s 2 s_1,s_2 s 1 , s 2
[ − R x 2 x 1 ] [ s 1 s 2 ] = t \begin{bmatrix}-Rx_2&x_1\end{bmatrix}\begin{bmatrix}s_1\\s_2\end{bmatrix}=t [ − R x 2 x 1 ] [ s 1 s 2 ] = t
因为上式是超定方程,可以用最小二乘法求解
x = ( A T A ) − 1 A T b x=(A^TA)^{-1}A^Tb x = ( A T A ) − 1 A T b
求解的s1和s2可能不再同一个坐标位置,一般取平均
问题
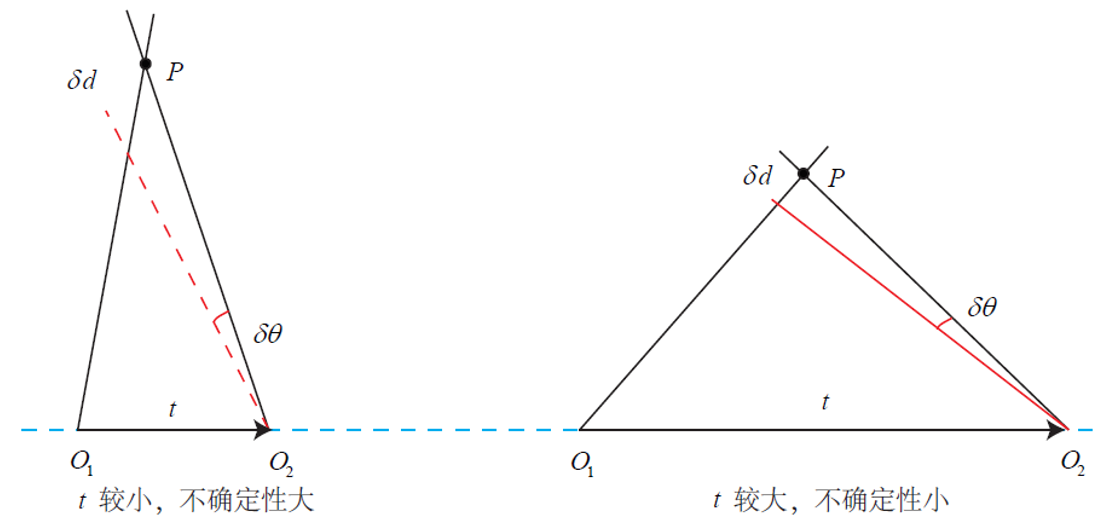
解得深度的质量与平移相关,平移小时误差的影响很大,但是平移大时特征匹配可能不成功
方程[ − R x 2 x 1 ] [ s 1 s 2 ] = t \begin{bmatrix}-Rx_2&x_1\end{bmatrix}\begin{bmatrix}s_1\\s_2\end{bmatrix}=t [ − R x 2 x 1 ] [ s 1 s 2 ] = t
系数矩阵伪逆不可靠
A T A A^TA A T A 例如,相机前进时,虽有位移,但是图像中心的点无法三角化,没有视差
特征点法的缺点,在提取特征点、特征匹配都比较耗时,匹配时丢弃了大量有用信息
计算VO的方法
关键点
描述子
方法
√
√
特征匹配
√
×
光流法、直接法
×
×
直接法
光流法:最小化重投影误差(Reprojection Error)
直接法:最小化光度误差(Photometric Error)
追踪原图像某个点在其他图像中的运动,本质是估计像素在不同时刻图像中的运动
光流分类
说明
算法
稀疏光流
计算部分像素运动
Lucas Kanade(LK)
稠密光流
计算几乎所有像素运动
Horn Schunck(HS)
设t时刻位于(x,y)处像素点的灰度值为
I ( x , y , t ) , I ∈ [ 0 , 255 ] I(x,y,t),I\in[0,255] I ( x , y , t ) , I ∈ [ 0 , 2 5 5 ]
设t时刻位于(x+dx,y+dy)处像素点的灰度值为
I ( x + d x , y + d y , t ) I(x+dx,y+dy,t) I ( x + d x , y + d y , t )
设t+dt时刻像素运动到了(x+dx,y+dy)处像素点的灰度值为
I ( x + d x , y + d y , t + d t ) I(x+dx,y+dy,t+dt) I ( x + d x , y + d y , t + d t )
希望计算运动( d x , d y ) (dx,dy) ( d x , d y )
灰度不变假设
在同一空间点的像素灰度值,在微笑时刻各个图像中是固定不变的I ( x + d x , y + d y , t + d t ) = I ( x , y , t ) I(x+dx,y+dy,t+dt)=I(x,y,t) I ( x + d x , y + d y , t + d t ) = I ( x , y , t )
这是理想情况下的假设,实际中由于高光/阴影/材质/曝光等不同,很可能不成立
对t+dt时刻的灰度值一阶泰勒展开:
I ( x + d x , y + d y , t + d t ) ≈ I ( x , y , t ) + ∂ I ∂ x d x + ∂ I ∂ y d y + ∂ I ∂ t d t I(x+dx,y+dy,t+dt)\approx I(x,y,t)+\frac{\partial I}{\partial x}dx+\frac{\partial I}{\partial y}dy+\frac{\partial I}{\partial t}dt I ( x + d x , y + d y , t + d t ) ≈ I ( x , y , t ) + ∂ x ∂ I d x + ∂ y ∂ I d y + ∂ t ∂ I d t
由于灰度不变原理,后面的导数项都为0
∂ I ∂ x d x + ∂ I ∂ y d y + ∂ I ∂ t d t = 0 \frac{\partial I}{\partial x}dx+\frac{\partial I}{\partial y}dy+\frac{\partial I}{\partial t}dt=0 ∂ x ∂ I d x + ∂ y ∂ I d y + ∂ t ∂ I d t = 0
可得,x和y方向梯度=I的时间变化梯度:∂ I ∂ x ∂ x ∂ t + ∂ I ∂ y ∂ y ∂ t = − ∂ I ∂ t \frac{\partial I}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial I}{\partial y}\frac{\partial y}{\partial t}=-\frac{\partial I}{\partial t} ∂ x ∂ I ∂ t ∂ x + ∂ y ∂ I ∂ t ∂ y = − ∂ t ∂ I
其中:
∂ x ∂ t \frac{\partial x}{\partial t} ∂ t ∂ x ∂ y ∂ t \frac{\partial y}{\partial t} ∂ t ∂ y ∂ I ∂ x \frac{\partial I}{\partial x} ∂ x ∂ I I x − 1 , y − I x + 1 , y 2 \frac{I_{x-1,y}-I_{x+1,y}}{2} 2 I x − 1 , y − I x + 1 , y ∂ I ∂ y \frac{\partial I}{\partial y} ∂ y ∂ I I x , y − 1 − I x , y + 1 2 \frac{I_{x,y-1}-I_{x,y+1}}{2} 2 I x , y − 1 − I x , y + 1 ∂ I ∂ t \frac{\partial I}{\partial t} ∂ t ∂ I
用矩阵表示上式:
[ I x I y ] [ u v ] = − I t \begin{bmatrix}I_x&I_y\end{bmatrix}\begin{bmatrix}u\\v\end{bmatrix}=-I_t [ I x I y ] [ u v ] = − I t
是一个欠定二元一次线型方程,需要引用额外的约束,假设窗口(w×w)内像素具有相同运动(光度不变),可以引入w 2 w^2 w 2
[ I x I y ] k [ u v ] = − I t k , k = 1 , ⋯ , w 2 \begin{bmatrix}I_x&I_y\end{bmatrix}_k\begin{bmatrix}u\\v\end{bmatrix}=-I_{tk},\;k=1,\cdots,w^2 [ I x I y ] k [ u v ] = − I t k , k = 1 , ⋯ , w 2 设A = [ [ I x , I y ] 1 ⋮ [ I x , I y ] k ] A=\begin{bmatrix}{[I_x,I_y]}_1\\\vdots\\{[I_x,I_y]}_k\end{bmatrix} A = ⎣ ⎢ ⎡ [ I x , I y ] 1 ⋮ [ I x , I y ] k ⎦ ⎥ ⎤ b = [ I t 1 ⋮ I t k ] b=\begin{bmatrix}I_{t1}\\\vdots\\I_{tk}\end{bmatrix} b = ⎣ ⎢ ⎡ I t 1 ⋮ I t k ⎦ ⎥ ⎤
A [ u v ] = − b A\begin{bmatrix}u\\v\end{bmatrix}=-b A [ u v ] = − b
当A可逆并且是方阵时:
[ u v ] = − A − 1 b \begin{bmatrix}u\\v\end{bmatrix}=-A^{-1}b [ u v ] = − A − 1 b
因为是超定方程,使用最小二乘法求解,使用伪逆形式:
[ u v ] ∗ = − ( A T A ) − 1 A T b \begin{bmatrix}u\\v\end{bmatrix}^*=-(A^TA)^{-1}A^Tb [ u v ] ∗ = − ( A T A ) − 1 A T b
可以看成最小化像素误差的话,可以用Gauss-Newton求解非线性优化问题
问题
光流依赖图像的梯度,但梯度不够平滑,可能会剧烈变化
局部梯度不能用于预测长期图像走向
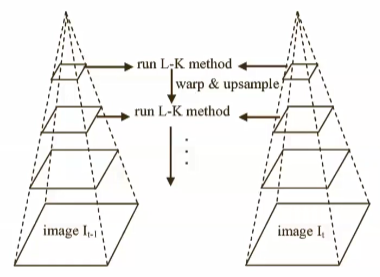
运动过快导致像素跟不上
解决方法
光流法仅估计了像素间的平移,没有用到相机本身的几何结构,相机的旋转和图像的缩放
跟踪在物体的边缘上,容易在跟踪时产生滑动
利用相机的运动关系,根据图像直接估计姿态变化,不再聚焦于某个像素,而是更加整体性的约束
设一点P(X,Y,Z),有两帧图像,有初始估计的R,t,用李群表示为e x p ( ξ ∧ ) exp(\xi^\wedge) e x p ( ξ ∧ )
I 1 ( p 1 ) ≈ I 2 ( p 2 ) I_1(p_1)\approx I_2(p_2) I 1 ( p 1 ) ≈ I 2 ( p 2 )
投影关系:
p 1 = [ u v 1 ] 1 = 1 Z 1 K P p_1=\begin{bmatrix}u\\v\\1\end{bmatrix}_1=\frac{1}{Z_1}KP p 1 = ⎣ ⎡ u v 1 ⎦ ⎤ 1 = Z 1 1 K P p 2 = [ u v 1 ] 2 = 1 Z 2 K ( R P + t ) = 1 Z 2 ( K e x p ( ξ ∧ ) P ) 1 : 3 p_2=\begin{bmatrix}u\\v\\1\end{bmatrix}_2=\frac{1}{Z_2}K(RP+t)=\frac{1}{Z_2}(Kexp(\xi^\wedge)P)_{1:3} p 2 = ⎣ ⎡ u v 1 ⎦ ⎤ 2 = Z 2 1 K ( R P + t ) = Z 2 1 ( K e x p ( ξ ∧ ) P ) 1 : 3 Z 1 Z 2 Z_1Z_2 Z 1 Z 2 因为e x p ( ξ ∧ ) exp(\xi^\wedge) e x p ( ξ ∧ ) 1 : 3 1:3 1 : 3
估计相机的运动,建立最小化光度误差问题:
min ξ J ( ξ ) = ∥ e ∥ 2 \min_\xi J(\xi)=\left\|e\right\|^2 min ξ J ( ξ ) = ∥ e ∥ 2 其中:
e e e Photometric Error,基于灰度不变假设(相机缓慢平移):
e = I 1 ( p 1 ) − I 2 ( p 2 ) e=I_1(p_1)-I_2(p_2) e = I 1 ( p 1 ) − I 2 ( p 2 )
ξ \xi ξ
在多个空间点的条件下:
min ξ J ( ξ ) = ∑ i = 1 N e i T e i \min_\xi J(\xi)=\sum_{i=1}^{N}e_i^Te_i min ξ J ( ξ ) = ∑ i = 1 N e i T e i e i = I 1 ( p 1 , i ) − I 2 ( p 2 , i ) e_i=I_1(p_1,i)-I_2(p_2,i) e i = I 1 ( p 1 , i ) − I 2 ( p 2 , i )
待估计的量为相机运动ξ \xi ξ ξ \xi ξ
求解最优解过程:使用李代数左乘扰动计算梯度,沿梯度方向求最优解
左乘扰动:e ( δ T ⊕ T ) = I 1 ( 1 Z 1 K P ) − I 2 ( 1 Z 2 K e x p ( δ ξ ∧ ) e x p ( ξ ∧ ) P ) e(\delta T\oplus T)=I_1(\frac{1}{Z_1}KP)-I_2(\frac{1}{Z_2}Kexp(\delta\xi^\wedge)exp(\xi^\wedge)P) e ( δ T ⊕ T ) = I 1 ( Z 1 1 K P ) − I 2 ( Z 2 1 K e x p ( δ ξ ∧ ) e x p ( ξ ∧ ) P )
对第二项做泰勒展开,用一阶近似:≈ I 1 ( 1 Z 1 K P ) − I 2 ( 1 Z 2 K ( 1 + δ ξ ∧ ) e x p ( ξ ∧ ) P ) = I 1 ( 1 Z 1 K P ) − I 2 ( 1 Z 2 K e x p ( ξ ∧ ) P + 1 Z 2 K δ ξ ∧ exp ( ξ ∧ ) P ) \approx I_1(\frac{1}{Z_1}KP)-I_2(\frac{1}{Z_2}K(1+\delta\xi^\wedge)exp(\xi^\wedge)P)=I_1(\frac{1}{Z_1}KP)-I_2(\frac{1}{Z_2}Kexp(\xi^\wedge)P+\frac{1}{Z_2}K\delta\xi^\wedge\exp(\xi^\wedge)P) ≈ I 1 ( Z 1 1 K P ) − I 2 ( Z 2 1 K ( 1 + δ ξ ∧ ) e x p ( ξ ∧ ) P ) = I 1 ( Z 1 1 K P ) − I 2 ( Z 2 1 K e x p ( ξ ∧ ) P + Z 2 1 K δ ξ ∧ exp ( ξ ∧ ) P )
为了简便,令:
q = δ ξ ∧ exp ( ξ ∧ ) P q=\delta\xi^\wedge\exp(\xi^\wedge)P q = δ ξ ∧ exp ( ξ ∧ ) P u = 1 Z 2 K q u=\frac{1}{Z_2}Kq u = Z 2 1 K q
I 1 ( 1 Z 1 K P ) − I 2 ( 1 Z 2 K e x p ( ξ ∧ ) P + u ) I_1(\frac{1}{Z_1}KP)-I_2(\frac{1}{Z_2}Kexp(\xi^\wedge)P+u) I 1 ( Z 1 1 K P ) − I 2 ( Z 2 1 K e x p ( ξ ∧ ) P + u ) 对第二项做泰勒展开,用一阶近似,可以链式法则求出I对x i xi x i ≈ I 1 ( 1 Z 1 K P ) − I 2 ( 1 Z 2 K e x p ( ξ ∧ ) P ) + ∂ I 2 ∂ u ∂ u ∂ q ∂ q ∂ ξ δ ξ \approx I_1(\frac{1}{Z_1}KP)-I_2(\frac{1}{Z_2}Kexp(\xi^\wedge)P)+\frac{\partial I_2}{\partial u}\frac{\partial u}{\partial q}\frac{\partial q}{\partial\xi}\delta\xi ≈ I 1 ( Z 1 1 K P ) − I 2 ( Z 2 1 K e x p ( ξ ∧ ) P ) + ∂ u ∂ I 2 ∂ q ∂ u ∂ ξ ∂ q δ ξ
= e ( ξ ) − ∂ I 2 ∂ u ∂ u ∂ q ∂ q ∂ ξ δ ξ =e(\xi)-\frac{\partial I_2}{\partial u}\frac{\partial u}{\partial q}\frac{\partial q}{\partial\xi}\delta\xi = e ( ξ ) − ∂ u ∂ I 2 ∂ q ∂ u ∂ ξ ∂ q δ ξ
其中:
∂ I 2 ∂ u \frac{\partial I_2}{\partial u} ∂ u ∂ I 2 ∂ u ∂ q \frac{\partial u}{\partial q} ∂ q ∂ u q = ( X , Y , Z ) T q=(X,Y,Z)^T q = ( X , Y , Z ) T
∂ u ∂ q = [ ∂ u ∂ X ∂ u ∂ Y ∂ u ∂ Z ∂ u ∂ X ∂ u ∂ X ∂ u ∂ X ] = [ f x Z 0 f x X Z 2 0 f y Z f y Y Z 2 ] \frac{\partial u}{\partial q}=\begin{bmatrix}\frac{\partial u}{\partial X}&\frac{\partial u}{\partial Y}&\frac{\partial u}{\partial Z}\\\frac{\partial u}{\partial X}&\frac{\partial u}{\partial X}&\frac{\partial u}{\partial X}\end{bmatrix}=\begin{bmatrix}\frac{f_x}{Z}&0&\frac{f_xX}{Z^2}\\0&\frac{f_y}{Z}&\frac{f_yY}{Z^2}\end{bmatrix} ∂ q ∂ u = [ ∂ X ∂ u ∂ X ∂ u ∂ Y ∂ u ∂ X ∂ u ∂ Z ∂ u ∂ X ∂ u ] = [ Z f x 0 0 Z f y Z 2 f x X Z 2 f y Y ]
∂ q ∂ ξ \frac{\partial q}{\partial\xi} ∂ ξ ∂ q
∂ q ∂ ξ = [ I , − q ∧ ] \frac{\partial q}{\partial\xi}=[I,-q\wedge] ∂ ξ ∂ q = [ I , − q ∧ ]
最终可得:
J = − ∂ I 2 ∂ u ∂ u ∂ δ ξ J=-\frac{\partial I_2}{\partial u}\frac{\partial u}{\partial \delta\xi} J = − ∂ u ∂ I 2 ∂ δ ξ ∂ u ∂ u ∂ δ ξ = − [ f x Z 0 − f x X Z 2 − f x X Y Z 2 f x + f x X 2 Z 2 − f x Y Z 0 f y Z − f y Y Z 2 − f y − f y Y 2 Z 2 f y X Y Z 2 f y X Z ] \frac{\partial u}{\partial \delta\xi}=-\begin{bmatrix}\frac{f_x}{Z}&0&-\frac{f_xX}{Z^2}&-\frac{f_xXY}{Z^2}&f_x+\frac{f_xX^2}{Z^2}&-\frac{f_xY}{Z}\\0&\frac{f_y}{Z}&-\frac{f_yY}{Z^2}&-f_y-\frac{f_yY^2}{Z^2}&\frac{f_yXY}{Z^2}&\frac{f_yX}{Z}\end{bmatrix} ∂ δ ξ ∂ u = − [ Z f x 0 0 Z f y − Z 2 f x X − Z 2 f y Y − Z 2 f x X Y − f y − Z 2 f y Y 2 f x + Z 2 f x X 2 Z 2 f y X Y − Z f x Y Z f y X ]
从式中可见有图像梯度因子,在图像中梯度不明显的地方,相机估计贡献就小
根据利用图像信息的不同,可分为:
稀疏直接法:利用角点或关键点
稠密直接法:使用所有像素
半稠密直接法:使用部分梯度明显的像素