长尾数据处理
过采样和重采样
每个Batch对每类样本设置比例,保证在一个Batch里是相对均衡的
- 大样本不能充分训练,导致准确率下降,同时小样本也容易过拟合
focal loss
- 通过减少易分类样本的权重,从而使得模型在训练时更专注于难分类的样本
- 假设一个二分类,样本x1属于类别1的pt=0.9,样本x2属于类别1的pt=0.6,显然前者更可能是类别1,假设γ=1,那么对于pt=0.9,调制系数则为0.1;对于pt=0.6,调制系数则为0.4,这个调制系数就是这个样本对loss的贡献程度,也就是权重,所以难分的样本(pt=0.6)的权重更大。
FL(pt)=−αt(1−pt)γlog(pt)
loss reweight
- loss reweight
- 如果对loss不加约束的话,大样本数据占主导,影响小样本,如果加约束的话,则会大大压缩大样本数据的训练,所以要找到一个中和的约束方法。这个模型想要可以区别major class和minor class,他的操作是在loss里面添加了一个和有效样本数量成反比的类平衡加权项。论文有两点贡献:
- 提供一种可以学习有效样本数量的方案来设计模型
- 提供了如何在sigmoid CE loss,softmax CE loss,focal loss上进行修改,并且通过实验验证提升
- 他引申出每个类都存在一个容量为N的特征空间S,那么每一群数量为n的样例都存在一个有效样本数量:En=1−β1−βn,β=NN−1
| 推导 |
结论 |
n=1 |
E1=1−β1−β=1 |
n=N-1 |
抽到以抽样样本概率P=NEn−1,En=PEn−1+(1−P)(En−1+1)=1+NN−1En−1,设En−1=1−β1−βn−1,En=En−1+(1−p),同时En=1−β1−βn,所以当样本为无穷大时,每一类容量为:N=limn→∞∑j=1Nβj−1=1−β1 |
| 推论 |
limβ→1En=N |
-
En的渐近性质表明,当N较大时,有效样本数与样本数N相同。在这种情况下,我们认为唯一原型数N较大,因此没有数据重叠,每个样本都是唯一的。在另一个极端,如果N = 1,这意味着我们相信存在一个单一的原型,所以这个类中的所有数据都可以通过这个原型通过数据扩充、转换等来表示。
-
现假设labely∈[1,2,…,C],C是总类别数,模型估计每一类的概率为:p=[p1,p2,…,pC]T,损失函数:L(p,y),每一类的有效采样数量:Eni=1−βi1−βini,βi=NNi−1,Ni=N,βi=β=NN−1
-
我们可以用En1来作为loss的权重,以CEloss为例:
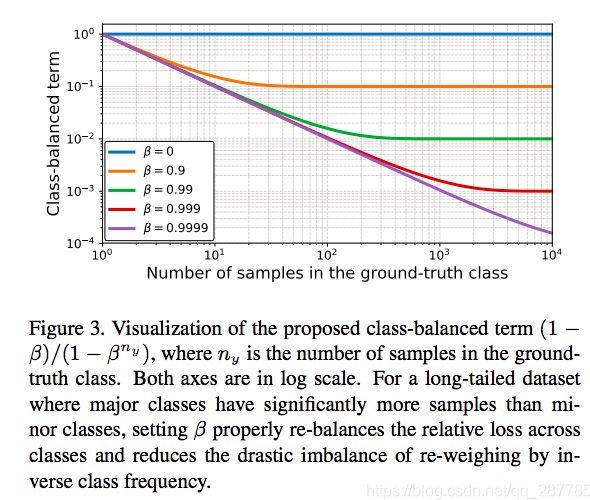
CB(p,y)=Eny1L(p,y)=1−βny1−βL(p,y)
- ny是每一类的采样数量,图3说明了不同的β,ny下,En1的输出
CEsoftmax(z,y)=−log(∑j=1Cexp(zj)exp(zy))
CBsoftmax(z,y)=−1−βny1−βlog(∑j=1Cexp(zj)exp(zy))
zit={zi,−zi,ifi=yotherwise
CEsigmoid(z,y)=−i=1∑Clog(sigmoid(zit))
CBsigmoid(z,y)=−1−β6ny1−βi=1∑Clog(sigmoid(zit))
FL(z,y)=−i=1∑C(1−pit)γlog(pit)
CB(z,y)=−1−βny1−βi=1∑C(1−pit)γlog(pit)


-
可以看到,根据数据集不同,β是变化的。N可以解释为一个类原始样本的数量。与粗粒度数据集相比,细粒度数据集的N应该更小。例如,一个特定鸟类物种的原始样本的数量应该小于一个通用鸟类类的原始的数量。由于CIFAR-100中的类比CIFAR-10更细粒度,所以CIFAR100的N应该比CIFAR-10小。这就解释了β的影响。
-
计算权重的时候,实际是按照每个类别样本数量作为n值,得到每个权重后需要归一化然后乘以class number。
i=1∑Cαi=C



