三维数学表达

点与坐标

点

点的表示

• 二维：$p(x,y)$
• 三维：$p(x,y,z)$

坐标系(参考系)

• 笛卡尔坐标系，三轴：x,y,z。向量的变换可以分为：平移、旋转、放缩

向量

向量表示

• 向量vector表示：$\overrightarrow{a}=(x,y)^T(e_1,e_2)$

向量运算

• 加减：$\overrightarrow{a}+\overrightarrow{b}=(a_x+b_x,a_y+b_y)$
• 内积：$a\cdot b=a^Tb=\sum_{i=1}^{3}a_ib_i=|a||b|cos(a,b)$
• 外积：$a\times b=\begin{bmatrix}i &j& k\\a_1 &a_2& a_3\\b_1 &b_2& b_3\\\end{bmatrix}=\begin{bmatrix}0 &-a_3& a_2\\a_3 &0& -a_1\\-a_2 &a_1& 0\\\end{bmatrix}b:=a^\wedge b$

向量旋转

• 内积(点乘)：$a\cdot b$表征了向量的投影
  • $a\cdot b=a^Tb=\sum_{i=1}^{3}a_ib_i=|a||b|cos(a,b)$
• 外积(叉乘)：$a\times b$表征了向量的旋转，a到b的旋转，可以使用右手定则，用w来描述。长度为：$|a||b|sin(a,b)$
  • $a\times b=\begin{bmatrix}i&j&k\\a_1&a_2&a_3\\b_1&b_2&b_3\end{bmatrix}=\begin{bmatrix}a_2b_3-a_3b_2\\a_3b_1-a_1b_3\\a_1b_2-a_2b_1\end{bmatrix}=\begin{bmatrix}0&-a_3&a_2\\a_3&0&-a_1\\-a_2&a_1&0\end{bmatrix}b:=a^\wedge b$
• 其中：$a^\wedge$是一个反对称矩阵，有很多特性
  • $A^T=-A$
  • $a^\wedge b=-b^\wedge a$

刚体运动

• 刚体：几何不变的物体
• 刚体运动：三维空间中，刚体做平移T、旋转R的运动

向量旋转和平移

旋转

旋转向量的推导

• 坐标系$(e_1,e_2,e_3)$中，P的坐标为$(a_1,a_2,a_3)$，P的向量可以表示做：$\begin{bmatrix} e_1,e_2,e_3\end{bmatrix}\begin{bmatrix} a_1\\a_2\\a_3\end{bmatrix}$

• 坐标系$(e_1,e_2,e_3)$中，同样的P坐标为$({a_1}',{a_2}',{a_3}')$，P的向量可以表示做：$\begin{bmatrix} {e_1}' ,{e_2}',{e_3}'\end{bmatrix}\begin{bmatrix} {a_1}'\\{a_2}'\\{a_3}'\end{bmatrix}$

• 由于都是表示同一个点P，可以建立下面的等式：

  • $\begin{bmatrix} e_1,e_2,e_3\end{bmatrix}\begin{bmatrix} a_1\\a_2\\a_3\end{bmatrix}=\begin{bmatrix} {e_1}' ,{e_2}',{e_3}'\end{bmatrix}\begin{bmatrix} {a_1}'\\{a_2}'\\{a_3}'\end{bmatrix}$

• 等式两边同左乘$\begin{bmatrix}e_1^T\\e_2^T\\e_3^T\end{bmatrix}$，由于e有性质：

  • $e_1^T\cdot e_1=1$
  • $e_1^T\cdot e_2=0$
  • $\begin{bmatrix}e_1^T\\e_2^T\\e_3^T\end{bmatrix}\begin{bmatrix} e_1,e_2,e_3\end{bmatrix}=I$

• 可以得到点P在e’坐标系下通过旋转矩阵R，变换到e坐标系的表示：

  • $\begin{bmatrix} a_1\\a_2\\a_3\end{bmatrix}=\begin{bmatrix} e_1^T{e_1}' &e_1^T{e_2}'&e_1^T{e_3}'\\e_2^T{e_1}' &e_2^T{e_2}'&e_2^T{e_3}'\\e_3^T{e_1}' &e_3^T{e_2}'&e_3^T{e_3}'\\\end{bmatrix}\begin{bmatrix} {a_1}'\\{a_2}'\\{a_3}'\end{bmatrix} := Ra'$

• R即旋转矩阵，必要条件：行列式为1的正交矩阵

• R的正交性质：1、$RR^T=I$，$R^{-1}=R^T$；2、$det(R)=1$

特殊正交群SO(n)

• SO(n)是Special Orthogonal Group，特殊正交群R
• $SO(n)=[R\in\mathbb{R}^{n\times n}|RR^T=I,det(R)=1]$
• 一般情况下n=3

旋转矩阵

• 旋转矩阵可以描述相机的运动，因为是正交阵，它的逆即转置，描述了一个相反的旋转
  • $a'=R^{-1}a=R^Ta$
• 于是，1和2相互旋转的关系为
  • $a_1=R_{12}a_2$
  • $a_2=R_{21}a_1$
  • 矩阵关系：$R_{21}=R_{12}^{-1}=R_{12}^T$
• $R_{12}^T$就表示一个相反方向的旋转

二维

• 在二维空间中，旋转可以用一个单一的角 定义。作为约定，正角表示逆时针旋转。把笛卡尔坐标的列向量关于原点逆时针旋转的矩阵是：
• $M(\theta)=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}=\cos\theta\begin{bmatrix}1&0\\0&1\end{bmatrix}+\sin\theta\begin{bmatrix}0&-1\\1&0\end{bmatrix}=exp(\theta\begin{bmatrix}0&-1\\1&0\end{bmatrix})$

三维

• 在三维空间中，旋转矩阵有一个等于单位1的实特征值。旋转矩阵指定关于对应的特征向量的旋转(欧拉旋转定理)。如果旋转角是 θ，则旋转矩阵的另外两个(复数)特征值是 exp(iθ) 和 exp(-iθ)。从而得出 3 维旋转的迹数等于 1 + 2 cos(θ)，这可用来快速的计算任何 3 维旋转的旋转角。
• 3 维旋转矩阵的生成元是三维斜对称矩阵。因为只需要三个实数来指定 3 维斜对称矩阵，得出只用三个是实数就可以指定一个 3 维旋转矩阵。

绕x-轴的主动旋转

• $R_x(\theta_x)=\begin{bmatrix}1&0&0\\0&\cos\theta_x&\sin\theta_x\\0&\sin\theta_x&\cos\theta_x\end{bmatrix}=exp(\theta\begin{bmatrix}0&0&0\\0&0&\theta_x\\0&\theta_x&0\end{bmatrix})$

绕y-轴的主动旋转

• $R_y(\theta_y)=\begin{bmatrix}\cos\theta_y&0&\sin\theta_y\\0&1&0\\-\sin\theta_y&0&\cos\theta_y\end{bmatrix}=exp(\theta\begin{bmatrix}0&0&\theta_y\\0&0&0\\-\theta_y&0&0\end{bmatrix})$

绕z-轴的主动旋转

• $R_z(\theta_z)=\begin{bmatrix}\cos\theta_z&-\sin\theta_z&0\\\sin\theta_z&\cos\theta_z&0\\0&0&1\end{bmatrix}=exp(\theta\begin{bmatrix}0&-\theta_z&0\\\theta_z&0&0\\0&0&0\end{bmatrix})$

平移

• 向量a经过旋转和平移后，得到完全描述的a’
• $a'=Ra+t$

欧拉定理(Euler’s rotation theorem)：刚体在三维空间里的一般运动，可分解为刚体上方某一点的平移，以及绕经过此点的旋转轴的转动

齐次变换

• 多次进行空间变换时：

  • $b=R_1a+t_1$
  • $c=R_2b+t_2=R_2(R_1a+t_1)+t_2$
  • …

• 当空间变换叠加次数很多时，那么计算会变得非常复杂。构造齐次坐标，将空间变换转为线性关系，就可以对增广矩阵进行叠加操作了

• $\begin{bmatrix} a'\\1\end{bmatrix} =\begin{bmatrix} R &t\\0^T&1\end{bmatrix} \begin{bmatrix} a\\1\end{bmatrix}:=T\begin{bmatrix} a\\1\end{bmatrix}$

• 定义T为变换矩阵(Transform Matrix)，$\widetilde{a}=\begin{bmatrix} a\\1\end{bmatrix}$，为了简便，使用a代替$\widetilde{a}$

• 变换矩阵T是在旋转矩阵R的基础上，做了齐次变换，放入了平移。

性质

• 齐次坐标中，某个点的每个分量同乘一个非零常数后，仍表示同一点

• $\widetilde{a}=\begin{bmatrix} a\\1\end{bmatrix}=\begin{bmatrix} ka\\k\end{bmatrix}=k\begin{bmatrix} a\\1\end{bmatrix}$

• 齐次坐标的线型关系

  • $\widetilde{b}=T_1\widetilde{a}$
  • $\widetilde{c}=T_2\widetilde{b}=T_2T_1\widetilde{a}$

• 逆变换矩阵：

  • $T^{-1}=\begin{bmatrix} R^T &-R^Tt\\0^T&1\end{bmatrix}$

特殊欧式群SE(n)

• SE(n)是Special Euclidean Group，特殊欧式群
• $SE(3)=[T=\begin{bmatrix} R &t\\0^T&1\end{bmatrix}\in\mathbb{R}^{4\times 4}|R\in SO(3),t\in\mathbb{R}^3]$

SO(3)和SE(3)

• SO(3)和SE(3)对加法不封闭(行列式为1的正交矩阵)：$R_1+R_2\notin SO(3)$，$T_1+T_2\notin SE(3)$

• SO(3)和SE(3)对乘法封闭：$R_1R_2\in SO(3)$，$T_1T_2\in SE(3)$

• 由于对SO(3)加法不封闭，那么求解最优值时，导数中$R+\triangle R\notin SO(3)$，这样无法叠加

旋转向量和欧拉角

• 前面用旋转矩阵表示3自由度的刚体旋转，3x3的矩阵包含9个变量，表示一个曲面，具有冗余的信息。

旋转向量

• 称为角轴/轴角(Angle Axis)或者旋转向量(Rotation Vector)
• 仅使用：方向(旋转轴)θ和长度(转过的角度)n表示的旋转向量
• 使用旋转向量θn更为简洁，但是具有歧义性，会有万向锁的问题。

罗德里格斯公式

• 罗德里格斯公式描(Rodrigues’s Formula)述了旋转向量到旋转矩阵的转换关系，通过罗德里格斯公式可以通过旋转向量θn，得到旋转矩阵R
• 假设一个旋转轴为n，角度为θ的旋转。旋转向量为θn，求R：
  • $R=cos\theta I+(1-cos\theta)nn^T+sin\theta n^\wedge$
• 罗德里格斯公式实际上是一个李代数，罗德里格斯的证明
• 证明

旋转矩阵求解旋转向量

• 通过旋转矩阵求旋转向量
  • $tr(R)=cos\theta tr(I)+(1-cos\theta)tr(nn^T)+sin\theta tr(n^\wedge)=1+2cos\theta$
• 角度：$\theta=arccos(\frac{tr(R)-1}{2})$
• 轴：$Rn=n$，轴在旋转时是不动的，通过求取$\lambda=1$的特征向量，就可以得到旋转轴n

欧拉角

• 旋转向量的轴并不容易找到，欧拉角通过三个坐标轴的方式，可以更直观的表示

• 三个旋转方向

  • 偏航(yaw)：z
  • 滚转(pitch)：y
  • 俯仰(roll)：x

• 通常按照z-y-x顺序转动，轴可以是定轴或动轴，不同领域习惯不同

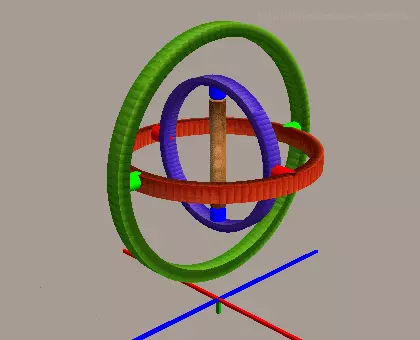
万向锁

• 旋转向量仅有三个实数表达旋转，不可避免的具有奇异性，是由于θ大于2π，相当于没有旋转，解决方法就是定义θ的范围
• 而欧拉角的奇异性问题，在特定值时，旋转自由度减1，和旋转顺序、角度有关，不太容易避免。欧拉角不适合插值或者迭代，通常用于人机交互中，比较直观

• 可以看到

  • 红色连接头：可以给予一个相对俯仰的自由度。
  • 绿色连接头：可以给予一个相对偏航的自由度。
  • 蓝色连接头：可以给予一个相对偏航的自由度。

• 在一定顺序的旋转后，三个连接头，提供的自由度只对应了俯仰和偏航两个自由度，桶滚自由度丢失了。

• 死锁的特点

  • 万向节死锁的根源在于欧拉角的定义方式
  • 万向节死锁的结果，不是说不能旋转了，而是会导致旋转不自然，前面的轴经过旋转后，卡在后面轴的旋转路径中了
  • 要规避万向节死锁，需要选择合适的旋转顺序（有12种旋转顺序）

• 在日常计算时，总会遇到万向锁问题。可以使用四元数解决

四元数

• 2维情况下，可以用单位复数表达旋转：
  • $z=x+iy=\rho e^{i\theta}$
  • 极坐标表示，模长乘极坐标的角度
• 乘i即旋转90°，乘-i旋转-90°
  • $zi=\rho e^{i\theta}i=\rho e^{i(\theta+\frac{\pi}{2})}$
• 四元数是一种三维情况下，扩充的复数表示旋转
• 四元数用四个实数表示旋转，既节省空间，同时避免了奇异性的问题

定义

• 四元数(Quaternion)q，拥有一个实部和三个虚部
• $q=q_0+q_1i+q_2j+q_3k$
• 可以用一个标量和一个向量表达四元数：$q=[s,v]$，$s=q_0\in\mathbb{R},v=[q_1,q_2,q_3]^T\in\mathbb{R}^3$

虚部

• $i^2=j^2=k^2=-1$
• $ij=k,ji=-k$
• $jk=i,kj=-i$
• $ki=j,ik=-j$

运算

• $q_a=[s_a,v_a]$，$q_b=[s_b,v_b]$
• 加减法：
  • $q_a\pm q_b=[s_a\pm s_b,v_a\pm v_b]$
• 乘法：
  • $q_aq_b=s_as_b-x_ax_b-y_ay_b-z_az_b+(s_ax_b+x_as_b+y_az_b-z_ay_b)i+(s_ay_b-x_az_b+y_as_b+z_ax_b)j+(s_az_b+x_ay_b-y_ax_a+z_as_b)k$
  • $=[s_as_b-v_a^Tv_b,s_av_b+s_bv_a+v_a\times v_b]$
  • ijk是有方向的，所以四元数乘法是不符合交换律的
• 共轭：
  • $q_a^*=s_a-x_ai-y_aj-z_ak=[s_a,-v_a]$
• 与共轭相乘：
  • $q_aq_a^*=q_a^*q_a=[s_a^2,v_a^Tv_a]$
• 模长：
  • $||q_a||=\sqrt{s_a^2+x_a^2+y_a^2+z_a^2}$
  • $||q_aq_b||=||q_bq_a||$
• 逆运算：
  • $q^{-1}=\frac{q^*}{||q||^2}$
  • $qq^{-1}=q^{-1}q=1$
  • $(q_aq_b)^{-1}=q_b^{-1}q_a^{-1}$
• 点积：
  • $q_a\cdot q_b=s_as_b+x_ax_bi+y_ay_bj+z_az_bk$

四元数对空间点旋转

• 三维点的旋转可以表示为$p'=Rp$
• 四元数p进行一次以四元数q表示的三维旋转，得到p’的表示：
  • 首先p的坐标用四元数表示(虚四元数)：$p=[0,x,y,z]=[0,v]$
  • 旋转的表示：$q=[cos\frac{\theta}{2},nsin\frac{\theta}{2}]^T$
  • 经过旋转后的关系为：$p'=qpq^{-1}=[0,x',y',z']=[0,v']$
    • p’是虚四元数的证明

四元数和欧拉角

• 如果通过四元数表示欧拉角，就可以解决万向锁的问题

旋转和四元数
![/images/pasted-381.png]

• 角轴到四元数

  • 三维空间的单位向量$n=[n_x,n_y,n_z]^T$，某个旋转是绕单位向量n进行了角度为θ的旋转，则该旋转四元数的表达形式为：
  • $q=[\cos{\frac{\theta}{2}},\mathbf{\omega}\sin{\frac{\theta}{2}}]^T$
  • $q=[cos\frac{\theta}{2},n_xsin\frac{\theta}{2},n_ysin\frac{\theta}{2},n_zsin\frac{\theta}{2}]^T=[cos\frac{\theta}{2},\vec{n}sin\frac{\theta}{2}]^T$

• 已知四元数q，反推夹角和旋转轴

  • $\theta=2arccosq_0$
  • $[n_x,n_y,n_z]^T=\frac{[q_1,q_2,q_3]^T}{sin\frac{\theta}{2}}$

旋转矩阵和四元数

• 假设：$q=q_0+q_1i+q_2j+q_3k$，$R=[m_{ij}],i,j\in[0,1,2]$

• 四元数到旋转矩阵

  • $R=\begin{bmatrix} 1-2q_2^2-2q_3^2& 2q_1q_2+2q_0q_3&2q_1q_3-2q_0q_2\\2q_1q_2-2q_0q_3 & 1-2q_1^2-2q_3^2&2q_2q_3+2q_0q_1\\2q_1q_3+2q_0q_2&2q_2q_3-2q_0q_1&1-2q12^2-2q_2^2\end{bmatrix}$

• 旋转矩阵到四元数

  • $q_0=\frac{\sqrt{tr(R)+1}}{2}$，$q_1=\frac{m_{23}-m_{32}}{4q_0}$，$q_2=\frac{m_{31}-m_{13}}{4q_0}$，$q_3=\frac{m_{12}-m_{21}}{4q_0}$

• 四元数通过旋转矩阵表示比较复杂，在实际应用中，q0比较小时其他三项会比较大，造成计算的不稳定

李群和李代数

• 由于SO和SE对加法不封闭，而求导操作需要加法运算，引入李代数的目的就是为了旋转矩阵的求导
• 李代数求导可以直接推出公式，但是要计算雅克比矩阵，另一种方式是左乘扰动模型，进行求解。

群

• 前面遇到了SO(3)和SE(3)，都属于群。
• $SO(3)=[R\in\mathbb{R}^{3\times 3}|RR^T=I,det(R)=1]$
• $SE(3)=[T=\begin{bmatrix} R &t\\0^T&1\end{bmatrix}\in\mathbb{R}^{4\times 4}|R\in SO(3),t\in\mathbb{R}^3]$

定义

• 群(G)是一种代数结构：集合(A)+运算(·)，即：G=(A,·)

群的特点

• 封闭性：
  • $\forall a_1,a_2\in A,\;a_1\cdot a_2\in A$
• 结合律：
  • $\forall a_1,a_2,a_3\in A,\;(a_1\cdot a_2)\cdot a_3=a_1\cdot (a_2\cdot a_3)$
• 幺元(单位元)：
  • $\exists a_0\in A,\; s.t.\;\forall a\in A,\;a_0\cdot a=a\cdot a_0=a$
• 逆：
  • $\forall a\in A,\;\exists a^{-1}\in A,\; s.t.\;a\cdot a^{-1}=a_0$

群的种类^[1]

• 一般线性群GL(n)：指n×n的可逆矩阵，它们对矩阵乘法成群

• 特殊正交群SO(n)：旋转矩阵和矩阵乘法，构成群，幺元是单位阵

• 特殊欧式群SE(n)：变换矩阵和矩阵乘法，构成群

• SO(n)和SE(n)加法不满足封闭性，旋转矩阵相加不满足约束，结构没有意义。

李群

• 李群(Lie Group)的特性
  • 具有连续(光滑)性质的群
  • 李群既是群，也是流形(光滑运动)
• SO(3)和SE(3)只有定义良好的乘法，没有加法，所以难以进行极限求导操作。
• SO(n):光滑的旋转，SE(n):光滑的旋转和移动

李群到李代数^[2]

• SO(3)和SE(3)在李群无法求导，原因是无法做加法，在曲空间做加法可能会掉到曲空间外面。而在切空间满足加法，可以利用李代数求得切空间，再映射到李群中去。

• 例如，一个特殊正交群，满足：$SO(3)=[R\in\mathbb{R}^{3\times 3}|RR^T=I,det(R)=1]$，其中R是相机的旋转，随时间t连续变化，可以描述为时间的函数：R(t)

• $R(t)R(t)^T=I$，连续运动就可以两边对t求导：

  • $\dot{R}(t)R^T(t) +R(t)\dot{R}^T(t)=0$
  • $\dot{R}(t)R^T(t)=-(\dot{R}(t)R^T(t))^T$，其中$\dot{R}(t)R^T(t)$是反对称矩阵，设为A
  • $A^T=-A,A=\dot{R}(t)R^T(t)$
  • A是反对称矩阵，反对称矩阵的形式：$A=\begin{bmatrix}0 &-a_3& a_2\\a_3 &0& -a_1\\-a_2 &a_1& 0\\\end{bmatrix}$
  • 设一个向量a表示为：$a=[a_1,a_2,a_3]^T$
  • 向量a可转为反对称矩阵A：$a^\wedge=A$，同样矩阵A也可转为向量a$A^\vee=a$

• 设$\phi(t)\in R^3$为三维向量，$\phi(t)^\wedge$为对应的反对称矩阵

• 则：$\dot{R}(t)R^T(t)=\phi(t)^\wedge$

• 两边同乘$R(t)$，因为R为正交阵，可得

  • $\dot{R}(t)R^T(t)R(t)=\dot{R}(t)$
  • $=\phi(t)^\wedge R(t)=\begin{bmatrix}0 &-\phi_3& \phi_2\\\phi_3 &0& -\phi_1\\-\phi_2 &\phi_1& 0\\\end{bmatrix}R(t)$
  • 此时，可以得到$\dot{R}(t)$导数形式了，而没有用到加法运算，而是乘了一个矩阵

• 考虑在单位元附近，令$t_0=0$，且$R(0)=I$，将$R(0)$在$t_0$处一阶泰勒展开：

  • $R(t)\approx R(t_0)+\dot{R}(t+0)(t-t_0)=I+\phi(t_0)^\wedge t$
  • $\phi$反映了一阶导数的性质，正切空间(tangent space)上，是位于单位元处的正切平面

• 根据上面得出的式子：

  • $\dot{R}(t)=\phi(t)^\wedge R(t)$
  • $\R(t)=I+\phi(t_0)^\wedge t$，一阶泰勒展开
  • $\phi(t_0)=\phi_0$，假设在$t_0$附近$\phi$不变
  • $R(0)=I$

• 假设在$t_0$附近$\phi$不变，在t=0附近时，就可以推出类似微分方程的式子：$\dot{R}(t)=\phi(t_0)^\wedge R(t)=\phi_0^\wedge R(t)$

• 一个函数导数等于其本身乘以一个矩阵，其与指数函数：$e^ax$导数形式一致，故可以写成如下形式：$R(t)=exp(\phi_0\wedge t)$

• 在李代数$\phi$任意一点，都可以通过指数映射$exp(\phi\wedge)$可以得到李群R，现在的目标就是求得向量$\phi$，矩阵的指数如何求$exp(\phi\wedge)$

李代数

• 李代数，与李群对应的一种结构，位于向量空间，是李群单位元处的正切空间，也就是导数形式
• 任意李群都对应一个李代数：SO(3)–>so(3)，SE(3)–>se(3)
• 李代数描述了李群单位元附近的正切空间性质，只是导数形式，李群转为李代数后就可以进行求导操作了。

定义

• 李代数有一个集合V，一个数域F和一个二元运算[,]组成

• 如果这三者满足下面的性质，称(V;F;[,])为一个李代数，记作$\mathfrak{g}$

  1. 封闭性：$\forall X,Y\in \mathbb{V} ,[X,Y]\in \mathbb{V}$
  2. 双线性：$\forall X,Y,Z\in \mathbb{V},\;a,b\in \mathbb{F}$，有：$[aX+bY,Z]=a[X,Z]+b[Y,Z],\;[Z,aX+bY]=a[Z,X]+b[Z,Y]$
  3. 自反性：$\forall X\in \mathbb{V},\;[X,X]=0$，李括号运算表示了两个元素的差异，度量X和X之间的差异
  4. 雅克比等价：$\forall X,Y,Z\in \mathbb{V},\;[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0$

• 其中二元运算也叫做李括号(Lie Bracket)，表示两个元素的差异。

  • 例如：三维空间向量+叉积运算，构成李代数

• 旋转矩阵李代数so(3)

  • $so(3)=[\phi\in R^3,\Phi=\phi\in R^{3\times 3}]$，$\Phi=\phi^\wedge=\begin{bmatrix}0 &-\phi_3& \phi_2\\\phi_3 &0& -\phi_1\\-\phi_2 &\phi_1& 0\\\end{bmatrix} \in R^{3\times 3}$
  • so(3)的李括号：$[\phi_1,\phi_2]=(\Phi_1\Phi_2-\Phi_2\Phi_1)^\vee$

• 变换矩阵李代数se(3)

  • $se(3)=[\xi=\begin{bmatrix}\rho\\\phi\end{bmatrix}\in \mathbb{R}^6,\rho\in \mathbb{R}^3,\phi\in so(3),\xi^\wedge=\begin{bmatrix}\phi^\wedge&\rho\\0^T&0\end{bmatrix}\in \mathbb{R}^{4\times 4}]$，李代数是6维的，前三维是平移，后三维是，$\Phi=\phi^\wedge=\begin{bmatrix}0 &-\phi_3& \phi_2\\\phi_3 &0& -\phi_1\\-\phi_2 &\phi_1& 0\\\end{bmatrix} \in R^{3\times 3}$
  • se(3)的李括号：$[\xi_1,\xi_2]=(\xi_1^\wedge\xi_2^\wedge-\xi_2^\wedge\xi_1^\wedge)^\vee$
    • 这里$\wedge$是将6维向量$\xi=\begin{bmatrix}\rho\\\phi\end{bmatrix}$转为4维矩阵$\xi^\wedge$，与稍有so(3)的不同：$\xi^\wedge=\begin{bmatrix} \phi^\wedge &\rho\\0^T&0\end{bmatrix}$

指数和对数映射

so(3)–>SO(3) 指数映射

• 旋转矩阵可以表示为指数形式：李代数到李群=指数形式

  • $R=exp(\phi\wedge)$

• 对于指数的泰勒展开为：

  • $exp(A)=\sum_{n=0}^{\infty}\frac{1}{n!}(A)^n$

• so(3)的泰勒展开：$exp(\phi^\wedge)=\sum_{n=0}^{\infty}\frac{1}{n!}(\phi^\wedge)^n$

• 由于$\phi$是向量，定义其方向a和模长$\theta$：$\phi=\theta a$

  • a的性质：
    1. 长度为1的单位向量，$||a||=1$；
    2. $a^\wedge a^\wedge=aa^T-I$；
    3. $a^\wedge a^\wedge a^\wedge=-a^\wedge$；

• a的性质，可以方便的对$exp(\phi^\wedge)$泰勒展开式进行化简：

  • $exp(\phi^\wedge)=\sum_{n=0}^{\infty}\frac{1}{n!}(\theta a^\wedge)^n$
  • $=I+\theta a^\wedge+\frac{1}{2!}\theta^2 a^\wedge a^\wedge+\dots$
  • $=aa^T+(\theta-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5+\dots)a\wedge -(1-\frac{1}{2!}\theta^2+\frac{1}{4!}\theta^4+\dots)a\wedge a\wedge$
  • $=cos\theta I+(1-cos\theta)aa^T+sin\theta a^\wedge$

• 最后指数映射的公式形式和罗德里格斯公式形式一致，所以说明李代数实际的物理意义就是旋转向量，李群实际的物理意义就是旋转矩阵。

• 罗德里格斯公式作用是由旋转向量转为旋转矩阵。

SO(3)–>so(3) 对数映射

• 如果反过来，也可以求得SO(3)到so(3)的元素，李群到李代数
• 求对数运算：
  • $\phi=\ln R^\vee=(\sum_{n=0}^{\infty}\frac{(-1)^n}{n+1}(R-I)^{n+1})^\vee$
• 用对数形式可以求解李代数，但是计算量太大。可以通过旋转矩阵直接求旋转向量的公式：$\theta=arccos(\frac{tr(R)-1}{2})$

se(3)–>SE(3)

• $exp(\xi^\wedge)=\begin{bmatrix}\sum_{n=0}^{\infty}\frac{1}{n!}(\phi^\wedge)^n&\sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^\wedge)^n\rho \\0^T &1 \end{bmatrix}:=\begin{bmatrix}R&J\rho\\o^T&1\end{bmatrix}=T$
• J是雅克比矩阵：$J=\frac{sin\theta}{\theta}+(1-\frac{sin\theta}{\theta})aa^T+\frac{1-cos\theta}{\theta}a^\wedge$

李代数的求导和扰动模型

• 李代数的求导方案：
  • 先利用李代数上加法定义李群元素的导数：$R\leftarrow\phi+\delta\phi$；
  • 再使用指数映射和对数映射完成变换关系：$e^{\phi_!^\wedge}e^{\delta\phi^\wedge}=exp^{(\phi_1+\delta\phi)^\wedge}$，需要判断是否相等：
• 式子在标量上明显成立：$e^ae^b=e^{a+b}$，但是在矩阵上不成立。
• 可以利用BCH进行线性近似，推导so(3)与se(3)上的导数和扰动模型，通常情况扰动模型更为简洁实用。

BCH公式

• Baker-Campbell-Hausdorff formula解释了两个李群的乘法再对数之后，得到李代数的加法展开的形式，方括号为李括号：
  • $ln(exp(A)exp(B))=A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[B,[A,B]]+...$
  • 完成公式形式
• 在SO(3)上，当$\phi_1\phi_2$其中一个量为小量时，忽略其高阶项，使用BCH简化为一阶线性近似形式：

$ln(e^{\phi_1^\wedge}e^{\phi_2^\wedge})^\vee\approx \begin{cases}J_l(\phi_2)^{-1}\phi_1+\phi_2 & \text{ if } \phi_1\;is\;small\\J_r(\phi_1)^{-1}\phi_2+\phi_1 & \text{ if } \phi_2\;is\;small\\\end{cases}$

• $\phi_1$是小量时，称为左雅克比

$J_l=J=\frac{sin\theta}{\theta}+(1-\frac{sin\theta}{\theta})aa^T+\frac{1-cos\theta}{\theta}a^\wedge$

$J_l^{-1}=\frac{\theta}{2}cot\frac{\theta}{2} I+(1-\frac{\theta}{2}cot\frac{\theta}{2})aa^T-\frac{\theta}{2} a^\wedge$

• $\phi_2$是小量时，称为右雅克比

$J_r(\phi)=J_l(-\phi)$

• 在李群上左乘小量时，李代数上的加法相差左雅克比的逆

$exp(\triangle\phi^\wedge)exp(\phi^\wedge)=exp((\phi+J_l^{-1}(\phi)\triangle\phi)^\wedge)$

• 李代数上进行小量加法时，相当于李群上左成一个带左雅克比的量，或者在李群上右乘一个带右雅克比的量

$exp((\phi+\triangle\phi)^\wedge)=exp((J_l\triangle\phi)^\wedge)exp(\phi^\wedge)=exp(\phi^\wedge)exp((J_r\triangle\phi)^\wedge$

• SE(3)同理

$exp(\triangle\xi^\wedge)exp(\xi^\wedge)=exp((J_l^{-1}\triangle\xi+\xi)^\wedge)$

$exp(\xi^\wedge)exp(\triangle\xi^\wedge)=exp((J_r^{-1}\triangle\xi+\xi)^\wedge$

扰动模型

• 通过BCG近似，可以定义李代数的导数了
• 假设机器人目前的位姿为T，观察点为p，产生乐意个观测数据z：$z=Tp+w$
• 误差为：$e=z-Tp$，对于N个连续观测，那么误差会叠加，估计位姿就是求解：$minJ(T)=\sum_{i=1}^{N}||z_i-Tp_i||_2^2$
• 求解J需要利用对R的导数，方法有两种：
  • 对R对应的李代数加上无限趋于0的$\delta\phi$小量，求相对于小量的李群的变化率，称为导数模型
  • 对R左乘或者右乘一个无限趋于0的$\delta R$小量，求相对于小量的李代数的变化率，称为左扰动和右扰动模型

导数模型

$R\leftarrow\phi+\delta\phi$

$\frac{\partial(exp(\phi^\wedge)p)}{\partial\phi}=\lim_{\delta\phi\rightarrow0}\frac{e^{(\phi+\delta\phi)^\wedge}p-e^{\phi^\wedge}p}{\delta\phi}$

$=-(Rp)^\wedge J_l$

• 需要求解雅克比矩阵，计算量比较大

扰动模型

$\frac{\partial(Rp)}{\partial\varphi}=\lim_{\varphi\rightarrow0}\frac{e^{\varphi^\wedge}e^{\phi^\wedge}p-e^{\phi\wedge}p}{\varphi}$

$=-(Rp)^\wedge$

• 扰动模型更为简单实用

---

1. 抽象代数：应用进阶代数 ↩︎

2. V.S. Varadarajan, Lie groups, Lie algebars, and their representations, vol. 102. Springer Science & Business Media, 2013. ↩︎