void land space 主页文章标签分类相册
eigen
| programme

eigen

Eigen简介

安装

linux

sudo apt-get install libeigen3-dev
  • 查找安装包，一般在/usr/include/eigen3
sudo updatedb
locate eigen3
  • 创建软连接
sudo ln -sf eigen3/Eigen Eigen
sudo ln -sf eigen3/unsupported unsupported

windows

vcpkg install eigen3

使用[1][2][3]

库与头文件

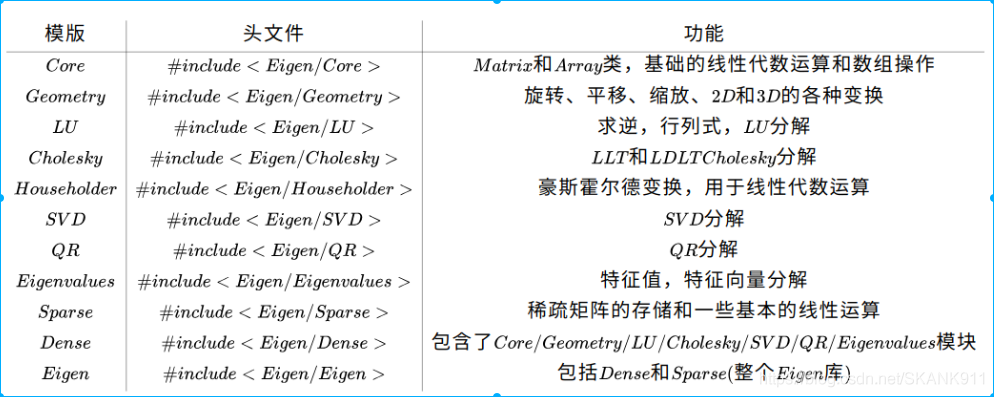
  • Eigen库被分为了一个Core模块和几个其他额外的模块，每个模块都有对应的头文件，使用时需要进行包含。其中通过Dense和Eigen头文件可以很方便的使用其他的模块，因此一般情况下使用这俩就够了。

库与头文件

Matrix类

  • 在Eigen中，所有的矩阵和向量都是Matrix模板类的对象，向量只是特殊的矩阵而已，无论是行向量还是列向量。

Matrix模板类

  • Matrix <typename Scalar,int RowsAtCompileTime,int ColsAtCompileTime,int Options=0,int MaxRowsAtCompileTime=RowsAtCompileTime,MaxColsAtCompileTime=ColsAtCompileTime>
  • Matrix类共有6个模板参数，主要使用的是前三个参数，剩余的都有默认值。前三个参数分别是<变量类型 ,行 , 列>
参数 说明
typename 变量类型
RowsAtCompileTime 行
ColsAtCompileTime 列
Options 是一个标志位，表明矩阵的存储方式，RowMajor表示按行存储。默认是按列存储的。例如：Matrix<float, 3, 3, RowMajor>
MaxRowsAtCompileTime 表示编译时矩阵尺寸的上限，主要是为了避免动态内存分配。
MaxColsAtCompileTime 矩阵尺寸列的上限

Matrix派生类对象

对象 定义
Vector3f typedef Matrix<float,3,1> Vector3f;
RowVector2i typedef Matrix<int,1,2> RowVector2i;
Matrix2d Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();//由轴角构造旋转向量，用于后面的由旋转向量构造李群
AngleAxisd 旋转向量：AngleAxisd ortation_vector(M_PI/4,Vector3d(0,0,1));沿z轴转45°
Quaterniond 四元数：Quaterniond q=Quaterniond(rotaion_vector)、Eigen::Quaterniond q(R);

参数Dynamic

  • RowsAtCompileTIme和ColsAtCompileTIme参数可以取特殊值Dynamic，这代表编译时不能确定矩阵的尺寸，必须在运行时确定。Eigen中称为动态尺寸，编译时确定尺寸的矩阵称为固定尺寸的矩阵
对象 定义
MatrixXd typedef Matrix <double，Dynamic，Dynamic> MatrixXd ;
VectorXi typedef Matrix <int，Dynamic，1> VectorXi ;

构造函数

  • 默认的构造函数不执行动态内存分配，也不初始化矩阵的元素。
Matrix3f a;  //a是3x3的矩阵，分配了float[9]的空间但是没有进行初始化
MatrixXf b; //b是个0x0的矩阵
  • 对于构造函数指定尺寸也是可以的，对于矩阵首先传递的是行参数，对于向量则只传递尺寸就好，构造函数会分配相应的空间但是不进行初始化工作。
MatrixXf a(10,15); //a是10x15的矩阵，分配了空间没有进行初始化
VectorXf b(30); //b是个尺寸为30的向量同样没有初始化
  • 尺寸小于4的向量可以直接在定义时初始化
Vector2d a（5.0,6.0）;
Vector3d b（5.0,6.0,7.0）;
Vector4d c（5.0,6.0,7.0,8.0）;

元素获取

MatrixXd m(2,2);
m(0,0)=3;m(1,0)=4;m(0,1)=5;m(1,1)=-3;
cout<<m<<endl;
MatrixXcf a = MatrixXcf::Random(2,2);
cout<<a<<endl;

逗号初始化

Matrix3f m;
m<< 1,2,3,
    4,5,6,
    7,8,9;
cout<<m<<endl;

调整尺寸

  • 矩阵的大小可以通过rows(), cols(), size()方法获取。对动态尺寸的矩阵调整尺寸时使用resize()方法
Matrix3d m(2,5);
m.resize(4,5);
cout<<m.rows()<<m.cols()<<m.size()<<endl;

Assignment和resizing

  • Assignment是将一个矩阵赋值给另一个，如果尺寸不同时Eigen会将左边的矩阵的尺寸自动resize成和右边的矩阵相同的尺寸
MatrixXf m(2,2);
cout<<m.rows()<<m.cols()<<m.size()<<endl;
MatrixXf n(3,3);
m = n;
cout<<n.rows()<<n.cols()<<n.size()<<endl;

固定尺寸VS动态尺寸

  • 对于小的矩阵，尤其是小于16个元素的，使用固定尺寸有利于代码性能，因为会避免动态内存的分配，固定尺寸的矩阵实际上就是个数组，

  • 比如Matrix4f mymatrix等价于float mymatrix[16]。

  • 而动态尺寸的矩阵总是在堆上申请内存，因此MatrixXf mymatrix[rows,cols]相当于float *mymatrix = new float[rows*cols]，并且MatrixXf对象还会存储它的行和列作为成员变量。

  • 使用固定尺寸的局限在于仅仅当你能提前确定矩阵的尺寸。对于较大的矩阵，如大于32,使用固定尺寸带来的性能效果就变得可以忽略了，更糟糕的是，当试图在函数内部创建一个很大的固定尺寸的矩阵时可能会导致栈溢出

矩阵与向量的运算

  • Eigen提供了一些矩阵和向量的数值运算，其中一些是通过通用的C++运算符重载实现，如+,-,*等，另一些通过特殊的方法实现，如dot()，cross()等方法。对于Matrix类，这些操作只支持线性代数运算，比如matrix1*matrix2代表矩阵的乘积，而向量+标量则是不允许的。

加减

  • 运算符两侧必须有相同的行和列。而且还要有相同的数据类型，因为Eigen并不做自动类型转换
可用的操作符 示例
二元运算+ a+b
二元运算- a-b
一元运算- -a
复合运算+= a+=b
复合运算-= a-=b

标量的乘除

可用的操作符 示例
二元运算符* matrix*scalar，scalar*matrix
二元运算符/ matrix/scalar
复合运算符*= matrix*=scalar
复合运算符/= matrix/=scalar

表达式模板

  • 不需要担心在Eigen中使用大的算法表达式。它仅仅是给了Eigen更多的优化机会。
  • Eigen中数值运算符如+并不执行任何计算，而是返回一个表达式对象描述需要执行的计算。一般是当整个表达式被评估完之后（典型的比如遇到符号=）实际的计算才进行。这样做主要是为了优化提高效率，比如当你写
VectorXf a(50), b(50), c(50), d(50);...a = 3*b + 4*c + 5*d;
  • Eigen会把他们编译成一个循环以便数组们只需要访问一次，比如会编译成如下形式
for(int i = 0; i < 50; ++i)
  a[i] = 3*b[i] + 4*c[i] + 5*d[i];

转置和共轭

  • 对矩阵的转置、共轭和共轭转置由成员函数transpose(), conjugate(), adjoint()实现
函数 说明
transpose() 转置a.transpose()
conjugate() 共轭a.conjugate()
adjoint() 共轭转置a.adjoint()
  • 对于实数矩阵，conjugate()不做任何操作，所以adjoint()等同于transpose()。
  • 基本的数值运算符、transpose()和adjoint()会简单的返回一个中间对象而不是对原对象做处理。
Matrix2i a;a<<1,2,3,4;
cout<<a<<endl;  //1,2\n3,4
a = a.transpose();//!!!不要这样做!!!
cout<<a<<endl; //1,2\n2,4
  • 这称为别名问题，在debug模式下当assertions没有禁止时，这种问题会被自动检测到。要避免错误，可以使用in-place转置。类似的还有adjointInPlace()。

矩阵相乘，矩阵乘向量

  • 矩阵相乘使用运算符*实现，由于向量也是一种特殊的矩阵，因此矩阵乘以向量和向量间的外积是一样的方法。所有这些情况都由两个运算符处理
可用的操作符 示例
二元运算符* a*b
复合运算符*= a*=b，等于a = a*b。

Eigen对矩阵相乘这种情况进行特殊处理，不用担心别名问题，比如m = m*m会被编译成tmp = m*m; m = tmp

点积和叉积

函数 说明
点积 v.dot(w)
叉积 v.cross(w)

基础的算术规约操作

  • Eigen提供了一些对于矩阵或向量的规约操作，
函数 说明
和 sum()
各元素相乘 prod()
矩阵行的最大值和索引 maxCoeff()
矩阵行的最小值和索引 minCoeff()
迹 trace为矩阵的迹，也可以由a.diagonal().sum()得到。

minCoeff和maxCoeff函数也可以返回相应的元素的位置信息

操作的有效性

  • Eigen会检查你的操作的有效性，如果可能的话会在编译阶段产生，输出信息。这些信息可能比较长并且难看，不过重要的信息都用了大写的语句标出了，可以很容易找到。如
Matrix3f m;
Vector4f v;
v = m*v;      // Compile-time error: YOU_MIXED_MATRICES_OF_DIFFERENT_SIZES
  • 但是另一些情况下，比如对于动态尺寸的检查不能在编译阶段完成，那么Eigen会在运行期间检查，如果出错，那么程序会崩溃并输出一些信息。
MatrixXf m(3,3);
VectorXf v(4);
v = m * v; // Run-time assertion failure here: "invalid matrix product"

实例

求解矩阵方程耗时比较（直接求逆，Qr分解，LU分解）

#include <iostream>
#include <ctime>
#include <Eigen/Core>
#include <Eigen/Dense>
#include <Eigen/LU>
#include <Eigen/Cholesky>
using namespace std;
using namespace Eigen;
/***********************
* solve equation: matrix_NN * x = v_Nd
************************/
const int MATRIX_SIZE = 100;
// https://blog.csdn.net/weixin_41074793/article/details/84241776
int main()
{
        Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;
        matrix_NN = MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
        Matrix<double, MATRIX_SIZE, 1> v_Nd;
        v_Nd = MatrixXd::Random( MATRIX_SIZE,1);
        clock_t time_stt = clock();
        //直接求逆
        Matrix< double, MATRIX_SIZE, 1> x = matrix_NN.inverse()*v_Nd;
        cout << "time use in normal inverse is       " << 1000.0 * (clock() - time_stt) /
                                (double)CLOCKS_PER_SEC << "ms" << endl;
        //Qr分解
        time_stt = clock();
        x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
        cout << "time use in Qr composition is       " << 1000 * (clock() - time_stt) / (double)
            CLOCKS_PER_SEC << "ms" << endl;
        //cholesky分解
        time_stt = clock();
        // 使得NN成为正定矩阵，才能分解
        matrix_NN = matrix_NN.transpose() * matrix_NN;
        x = matrix_NN.partialPivLu().solve(v_Nd);
        cout << "time use in cholesky composition is " << 1000 * (clock() - time_stt) / (double)
            CLOCKS_PER_SEC << "ms" << endl;
        //LU分解
        time_stt = clock();
        x = matrix_NN.partialPivLu().solve(v_Nd);
        cout << "time use in LU composition is       " << 1000 * (clock() - time_stt) / (double)
            CLOCKS_PER_SEC << "ms" << endl;
    return 0;
}

矩阵使用的案例

  • 视觉slam十四讲中的
#include <iostream>
using namespace std;
#include <ctime>
// Eigen 部分
#include <Eigen/Core>
// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Dense>
#define MATRIX_SIZE 50
int main( int argc, char** argv )
{
    // Eigen 中所有向量和矩阵都是Eigen::Matrix，它是一个模板类。它的前三个参数为：数据类型，行，列
    // 声明一个2*3的float矩阵
    Eigen::Matrix<float, 2, 3> matrix_23;
    // 同时，Eigen 通过 typedef 提供了许多内置类型，不过底层仍是Eigen::Matrix
    // 例如 Vector3d 实质上是 Eigen::Matrix<double, 3, 1>，即三维向量
    Eigen::Vector3d v_3d;
	// 这是一样的
    Eigen::Matrix<float,3,1> vd_3d;
    // Matrix3d 实质上是 Eigen::Matrix<double, 3, 3>
    Eigen::Matrix3d matrix_33 = Eigen::Matrix3d::Zero(); //初始化为零
    // 如果不确定矩阵大小，可以使用动态大小的矩阵
    Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > matrix_dynamic;
    // 更简单的
    Eigen::MatrixXd matrix_x;
    // 这种类型还有很多，我们不一一列举
    // 下面是对Eigen阵的操作
    // 输入数据（初始化）
    matrix_23 << 1, 2, 3, 4, 5, 6;
    // 输出
    cout << matrix_23 << endl;
    // 用()访问矩阵中的元素
    for (int i=0; i<2; i++) {
        for (int j=0; j<3; j++)
            cout<<matrix_23(i,j)<<"\t";
        cout<<endl;
    }
    // 矩阵和向量相乘（实际上仍是矩阵和矩阵）
    v_3d << 3, 2, 1;
    vd_3d << 4,5,6;
    // 但是在Eigen里你不能混合两种不同类型的矩阵，像这样是错的
    // Eigen::Matrix<double, 2, 1> result_wrong_type = matrix_23 * v_3d;
    // 应该显式转换
    Eigen::Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;
    cout << result << endl;
    Eigen::Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;
    cout << result2 << endl;
    // 同样你不能搞错矩阵的维度
    // 试着取消下面的注释，看看Eigen会报什么错
    // Eigen::Matrix<double, 2, 3> result_wrong_dimension = matrix_23.cast<double>() * v_3d;
    // 一些矩阵运算
    // 四则运算就不演示了，直接用+-*/即可。
    matrix_33 = Eigen::Matrix3d::Random();      // 随机数矩阵
    cout << matrix_33 << endl << endl;
    cout << matrix_33.transpose() << endl;      // 转置
    cout << matrix_33.sum() << endl;            // 各元素和
    cout << matrix_33.trace() << endl;          // 迹
    cout << 10*matrix_33 << endl;               // 数乘
    cout << matrix_33.inverse() << endl;        // 逆
    cout << matrix_33.determinant() << endl;    // 行列式
    // 特征值
    // 实对称矩阵可以保证对角化成功
    Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> eigen_solver ( matrix_33.transpose()*matrix_33 );
    cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
    cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;
    // 解方程
    // 我们求解 matrix_NN * x = v_Nd 这个方程
    // N的大小在前边的宏里定义，它由随机数生成
    // 直接求逆自然是最直接的，但是求逆运算量大
    Eigen::Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;
    matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
    Eigen::Matrix< double, MATRIX_SIZE,  1> v_Nd;
    v_Nd = Eigen::MatrixXd::Random( MATRIX_SIZE,1 );

    clock_t time_stt = clock(); // 计时
    // 直接求逆
    Eigen::Matrix<double,MATRIX_SIZE,1> x = matrix_NN.inverse()*v_Nd;
    cout <<"time use in normal inverse is " << 1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC << "ms"<< endl;
	// 通常用矩阵分解来求，例如QR分解，速度会快很多
    time_stt = clock();
    x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
    cout <<"time use in Qr decomposition is " <<1000*  (clock() - time_stt)/(double)CLOCKS_PER_SEC <<"ms" << endl;
    return 0;
}

几何模块

#include <iostream>
#include <cmath>
using namespace std;
#include <Eigen/Core>
// Eigen 几何模块
#include <Eigen/Geometry>
int main ( int argc, char** argv )
{
    // Eigen/Geometry 模块提供了各种旋转和平移的表示
    // 3D 旋转矩阵直接使用 Matrix3d 或 Matrix3f
    Eigen::Matrix3d rotation_matrix = Eigen::Matrix3d::Identity();
    // 旋转向量使用 AngleAxis, 它底层不直接是Matrix，但运算可以当作矩阵（因为重载了运算符）
    Eigen::AngleAxisd rotation_vector ( M_PI/4, Eigen::Vector3d ( 0,0,1 ) );     //沿 Z 轴旋转 45 度
    cout .precision(3);
    cout<<"rotation matrix =\n"<<rotation_vector.matrix() <<endl;                //用matrix()转换成矩阵
    // 也可以直接赋值
    rotation_matrix = rotation_vector.toRotationMatrix();
    // 用 AngleAxis 可以进行坐标变换
    Eigen::Vector3d v ( 1,0,0 );
    Eigen::Vector3d v_rotated = rotation_vector * v;
    cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;
    // 或者用旋转矩阵
    v_rotated = rotation_matrix * v;
    cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;
    // 欧拉角: 可以将旋转矩阵直接转换成欧拉角
    Eigen::Vector3d euler_angles = rotation_matrix.eulerAngles ( 2,1,0 ); // ZYX顺序，即roll pitch yaw顺序
    cout<<"yaw pitch roll = "<<euler_angles.transpose()<<endl;
    // 欧氏变换矩阵使用 Eigen::Isometry
    Eigen::Isometry3d T=Eigen::Isometry3d::Identity();                // 虽然称为3d，实质上是4＊4的矩阵
    T.rotate ( rotation_vector );                                     // 按照rotation_vector进行旋转
    T.pretranslate ( Eigen::Vector3d ( 1,3,4 ) );                     // 把平移向量设成(1,3,4)
    cout << "Transform matrix = \n" << T.matrix() <<endl;
    // 用变换矩阵进行坐标变换
    Eigen::Vector3d v_transformed = T*v;                              // 相当于R*v+t
    cout<<"v tranformed = "<<v_transformed.transpose()<<endl;
    // 对于仿射和射影变换，使用 Eigen::Affine3d 和 Eigen::Projective3d 即可，略
    // 四元数
    // 可以直接把AngleAxis赋值给四元数，反之亦然
    Eigen::Quaterniond q = Eigen::Quaterniond ( rotation_vector );
    cout<<"quaternion = \n"<<q.coeffs() <<endl;   // 请注意coeffs的顺序是(x,y,z,w),w为实部，前三者为虚部
    // 也可以把旋转矩阵赋给它
    q = Eigen::Quaterniond ( rotation_matrix );
    cout<<"quaternion = \n"<<q.coeffs() <<endl;
    // 使用四元数旋转一个向量，使用重载的乘法即可
    v_rotated = q*v; // 注意数学上是qvq^{-1}
    cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;
    return 0;
}

  1. 链接 ↩︎

  2. 链接 ↩︎

  3. 链接 ↩︎

robotic