简介
介绍
- 三维视觉相较于二维视觉增加了深度信息,可以更好的利用环境信息,为物体分类、目标检测、场景分割等任务提供更多的信息。
三维表达
- 三维表达的方法
| 三维表达 | 说明 |
|---|---|
| point cloud | 点云 |
| mesh | 三角形或三变形面片组合 |
| volumetric | 栅格化 |
| projected view RGB(D) | 图片拼接,具有RGB信息 |
| Voxel Grid | 体素网格 |
| Octree | 八叉树 |
- 体素网格冗余信息过多,很多空间实际上是空的,但仍会占据存储空间。八叉树很好的解决了这个问题
- 点云容易表达,可以使用矩阵表示,但是也有很多的缺点:
- 点云的点密度近密远疏,不均匀
- 与二维图像相比,不容易找到最近邻的点
- 没有纹理信息
- 顺序无关性,点云中的点排列顺序是没有关系的
- 旋转物体后的点云是变化的,但是还是代表一个物体
处理的方法
-
基于结构化网格
- Voxel based:体素化
- multiview based:多视角投影为二维图处理
-
点云直接处理
-
基于图的方法
数据集
| 形状分类的数据集 | samples | classes | type | representation |
|---|---|---|---|---|
| McGill Benchmark | 456 | 19 | Synthetic | Mesh |
| Sydney Urban Objects | 588 | 14 | Real-World | point cloud |
| ModelNet10 | 4899 | 10 | Synthetic | Mesh |
| ModelNet40 | 12311 | 40 | Synthetic | Mesh |
| ShapeNet | 51190 | 55 | Synthetic | Mesh |
| ScanNet | 12283 | 17 | Real-World | RGB-D |
| ScanObjectNN | 2902 | 15 | Real-World | point cloud |
| 目标检测和跟踪数据集 | scenes | classes | type | representation |
|---|---|---|---|---|
| KITTI | 22 | 8 | Urban(driving) | RGB&LiDAR |
| SUN RGB-D | 47 | 37 | Indoor | RGBD |
| ScanNetV2 | 1.5K | 18 | Indoor | RGBD&Mesh |
| H3D | 160 | 8 | Urban(driving) | RGB&LiDAR |
| Argoverse | 113 | 15 | Urban(driving) | RGB&LiDAR |
| Lyft L5 | 366 | 9 | Urban(driving) | RGB&LiDAR |
| A*3D | - | 7 | Urban(driving) | RGB&LiDAR |
| Waymo Open | 1K | 4 | Urban(driving) | RGB&LiDAR |
| nuScenes | 1K | 23 | Urban(driving) | RGB&LiDAR |
| 3d点云分割数据集 | points | classes | RGB | sensors |
|---|---|---|---|---|
| Oakland | 1.6M | 5(44) | N/A | MLS |
| ISPRS | 1.2M | 9 | N/A | ALS |
| Paris-rue-Madame | 20M | 17 | N/A | MLS |
| IQmulus | 300M | 8(22) | N/A | MLS |
| ScanNet | - | 20(20) | Yes | RGBD |
| S3DIS | 273M | 13(13) | Yes | Matterport |
| Semantic3D | 4000M | 8(9) | Yes | TLS |
| Paris-Lile-3D | 143M | 9(50) | N/A | MLS |
| SemanticKITTI | 4549M | 25(28) | N/A | MLS |
| Toronto-3D | 78.3M | 8(9) | Yes | MLS |
| DALES | 505M | 8(9) | N/A | ALS |
传统算法
奇异值分解SVD[1]
-
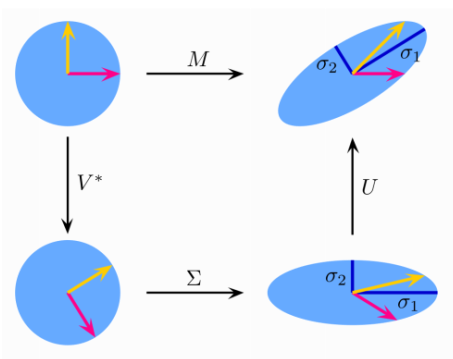
奇异值分解在数据降维中有较多的应用,这里把它的原理简单总结一下,并且举一个图片压缩的例子,最后做一个简单的分析,希望能够给大家带来帮助。
-
上图初始是I为圆形,两种变化的途径
- 第一种:经过M进行了旋转缩放变化,变成了椭圆
- 第二种:依次经过:旋转矩阵–>缩放矩阵–>旋转矩阵,变换为椭圆
特征值分解(EVD)
实对称矩阵
- 在理角奇异值分解之前,需要先回顾一下特征值分解,如果矩阵A是一个m×m的实对称矩阵(即),那么它可以被分解成如下的形式
- (1-1)
- 其中Q为标准正交阵,即有,Σ为对角矩阵,且上面的矩阵的维度均为m×m。λi称为特征值,qi是Q(特征矩阵)中的列向量,称为特征向量。
一般矩阵
- 上面的特征值分解,对矩阵有着较高的要求,它需要被分解的矩阵A为实对称矩阵,但是现实中,我们所遇到的问题一般不是实对称矩阵。那么当我们碰到一般性的矩阵,即有一个m×n的矩阵A,它是否能被分解成上面的式(1-1)的形式呢?当然是可以的,这就是我们下面要讨论的内容。
奇异值分解(SVD)
奇异值分解定义
- 有一个m×n的实数矩阵A,我们想要把它分解成如下的形式:
- 其中U和V均为单位正交阵,即有和,U称为左奇异矩阵,V称为右奇异矩阵,Σ仅在主对角线上有值,我们称它为奇异值,其它元素均为0。上面矩阵的维度分别为, , 。
- 一般地Σ有如下形式
奇异值求解
-
正常求上面的U,V,Σ不便于求,我们可以利用如下性质:
- (2-2)
- (2-3)
- 注:需要指出的是,这里与在矩阵的角度上来讲,它们是不相等的,因为它们的维数不同,而,但是它们在主对角线的奇异值是相等的
- ,
-
可以发现和也是对称矩阵,那么可以利用式(1-1),做特征值分解。利用式(2-2)特征值分解,得到的特征矩阵即为U;利用式(2-3)特征值分解,得到的特征矩阵即为V;对或中的特征值开方,可以得到所有的奇异值。
举例
- 假设已知矩阵A:
- 就可以求出的特征值分解U、的特征值分解V,得到的特征值的开方,最终求得
import numpy as np |
- SVD做图像压缩
import matplotlib.pyplot as plt |
- 可以看到,当我们取到前面120个奇异值来重构图片时,基本上已经看不出与原图片有多大的差别。
谱定理spectral theorem
- 谱定理是线性代数中很重要很基础的定理,并为以后的特征值分解做准备
- 谱定理:设A是nxn满秩对称矩阵,存在正交向量u,,满足下面的等式:
- 其中:
瑞利商
- Rayleigh Quotient定义函数为瑞丽商
- 其中x为非零向量,而A为n×n的Hermitan矩阵。所谓的Hermitan矩阵就是满足共轭转置矩阵和自己相等的矩阵,即。如果我们的矩阵A是实矩阵,则满足的矩阵即为Hermitan矩阵。
- 瑞利商有一个非常重要的性质,即它的最大值等于矩阵A最大的特征值,而最小值等于矩阵A的最小的特征值,也就是满足
- 解释瑞丽商就是:经过x和xT旋转变换后的最大最小值是多少,旋转不会改变特征值的大小
- 当向量x是标准正交基时,即满足时,瑞利商退化为:,这个形式在谱聚类和PCA中都有出现。
结合谱定理
- U是正交的,是对角
- 根据瑞丽商:
- x经过U的旋转变为,特征值是不变的,所以
- 结合上面的式子,可得瑞丽商
PCA
-
主成分分析是一种无监督降维的方法
-
定义输入:
-
输出:主成分向量,投影到主成分向量上,方差最大
-
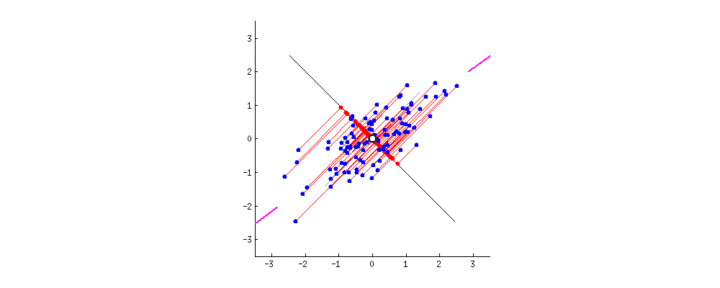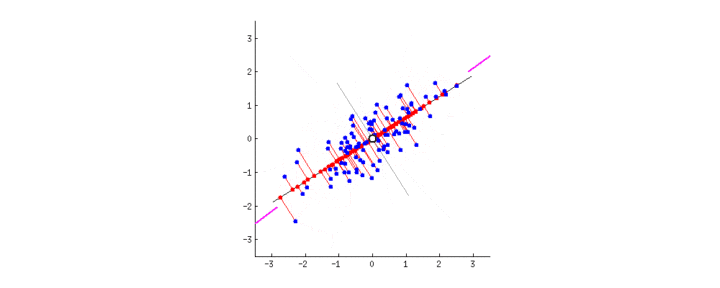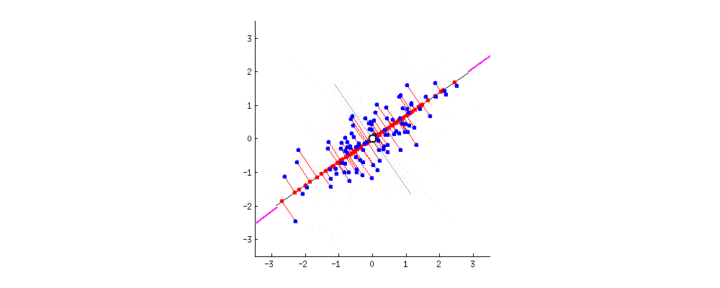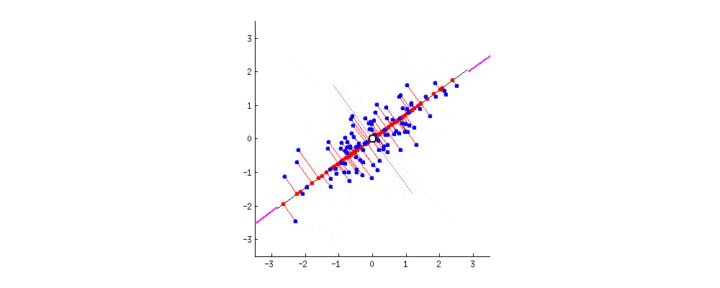
PCA的目的是找到线性不相关的正交轴,这些正交轴也称为m维空间中的主成分(PC),以将数据点投影到这些PC上。第一台PC捕获数据中最大的差异。让我们通过将PCA拟合到2D数据矩阵上来直观地了解PCA,该矩阵可以方便地用2D散点图表示:
-
由于所有PC彼此正交,因此我们可以在二维空间中使用一对垂直线作为两台PC。为了使第一台PC捕获最大的方差,我们旋转我们的PC对以使其其中的一个与数据点的分布最佳对齐。接下来,所有数据点都可以投影到PC上,它们的投影(PC1上的红色点)本质上是数据集降维的结果。中提琴,我们只是将矩阵从2-D缩减为1-D,同时保留了最大的方差!
-
可以通过协方差矩阵C的特征分解来确定PC。毕竟,特征分解的几何意义是通过旋转找到C的特征向量的新坐标系。
-
假设C的特征向量组成的矩阵为W, 特征值组成的对角矩阵为 [公式] ,则有如下公司成立:
-
在上式中,协方差矩阵C(m×m)被分解为特征向量W(m×m)的矩阵和m个特征值Λ的对角矩阵。特征向量是W中的列向量,实际上是我们要寻找的PC。然后,我们可以使用矩阵乘法将数据投影到PC空间上。出于降维的目的,我们可以将数据点投影到前k个PC上,作为数据的表示形式:
-
以二维特征为例,两个特征之间可能存在线性关系的(例如这两个特征分别是运动的时速和秒速度),这样就造成了第二维信息是冗余的。PCA的目标是为了发现这种特征之间的线性关系,检测出这些线性关系,并且去除这线性关系。
-
定义两个特征之间的协方差:
- 多个特征之间的协方差矩阵:
-
where
-
根据协方差矩阵,求出特征值、特征向量,找到对应特征值较大的k个特征向量组合成为变换矩阵,说明这k个特征值在整个特征空间是比较重要的。通过矩阵乘法,我们就把原样本空间压缩了。
特点
- 降维
- 法向量的估计
kernel PCA
-
输入有时不能通过线型分类器进行分类,如果可以升维操作,就可以实现线性操作进行分类了
-
步骤与PCA相同
-
输入,非线性映射
- 假设是均值为0的分布
- 计算协方差矩阵:
- 求解特征向量和特征值:
-
kernel的选择:
| kernel | 说明 |
|---|---|
| Linear | |
| Polynomial | |
| Gaussian | |
| Laplacian |
寻找法向量
- 用曲线拟合点云数据,曲面上任意一点,都可以找到切平面,只要能够获取切平面的法向量。
- 如何找法向量,PCA寻找的是最有用的向量,方差最大,而法向量则找最没用的向量,分布最集中。具体步骤
- 选择一个点
- 定义一个邻域
- PCA
- 寻找对应特征值最小的特征向量
- 同时得到曲率:
邻域的选择
- 邻域大小的选择非常重要,大邻域值可以避免误差,但会降低精细程度,导致法向量不准确;小邻域对模型表达更精准,但容易被噪声影响
- 提升的方式:
- 根据信息的特征选择比较类似的邻域,例如RGBD颜色、Lidar反射率,在每个点增加权重属性
- RANSAC
- DeepLearning
深度学习
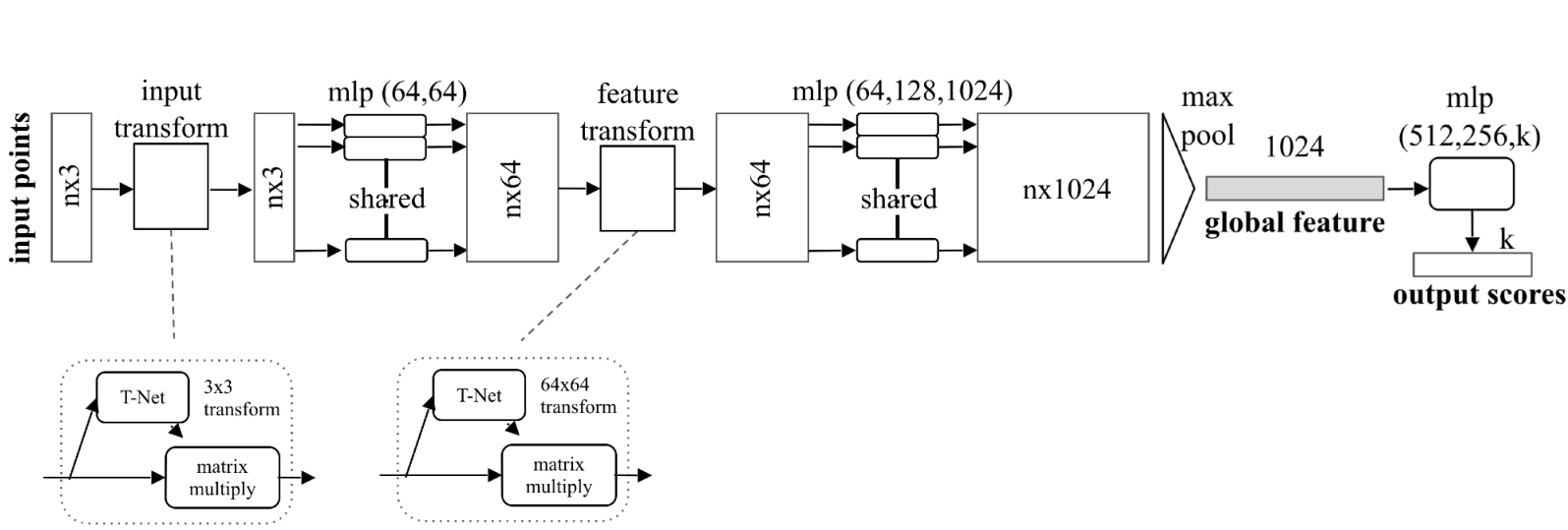
PointNet
-
PointNet,2016。直接使用点云数据进行分类、分割的目标。
-
之前处理点云的方法
- 可以栅格化后,通过3D-CNN处理,例如VoxNet算法;
- 通过投影,得到图像,通过2D-CNN识别,例如Multi-view CNN
- 抽取特征,通过全连接网络处理
-
PointNet就直接利用点云数据进行处理,实现分类、分割等操作。
-
利用点云,模型会遇到两个挑战:
- 模型顺序无关性
- 模型几何不变性
模型顺序无关性
- 对称函数满足顺序无关,例如:max()、sum()等函数。
- 神经网络中的复合函数,共享的h(x)函数使用MLP将输入转换为高维向量,减少后续g(x)池化的维度丢失的问题
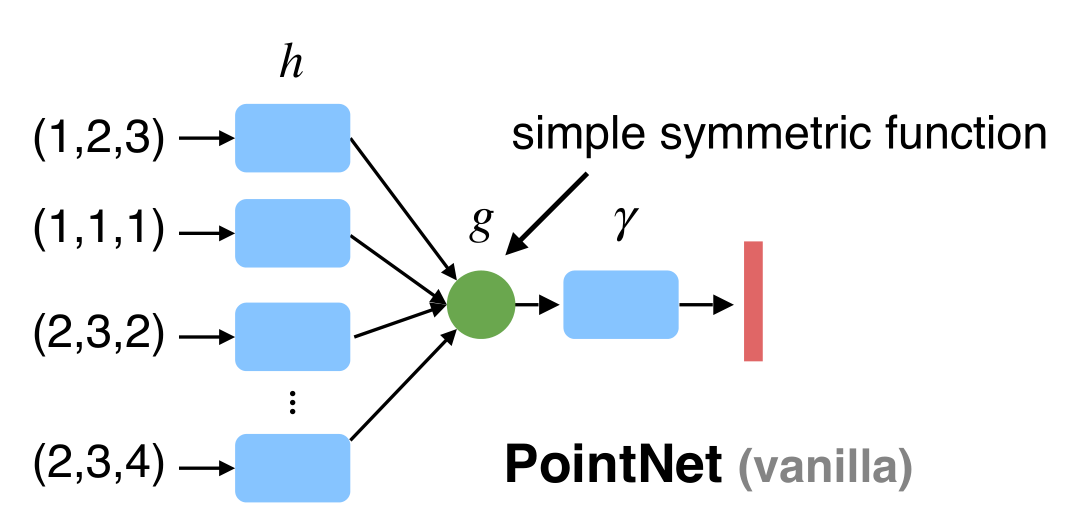
- 作者证明:PointNet可以拟合任意的连续函数
模型几何不变性
- 引入变换网络,通过矩阵乘法,使得模型可以自动找到旋转的角度,适应目标的识别。
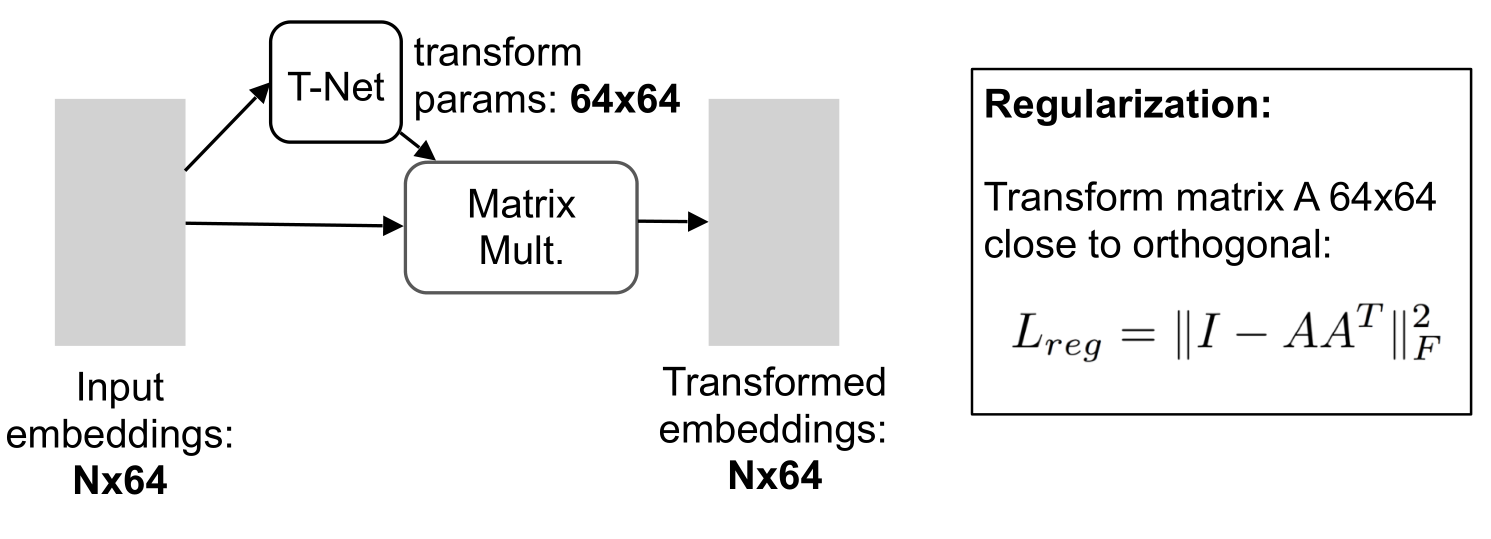
- 其中T-Net可以用mlp实现。
整体模型
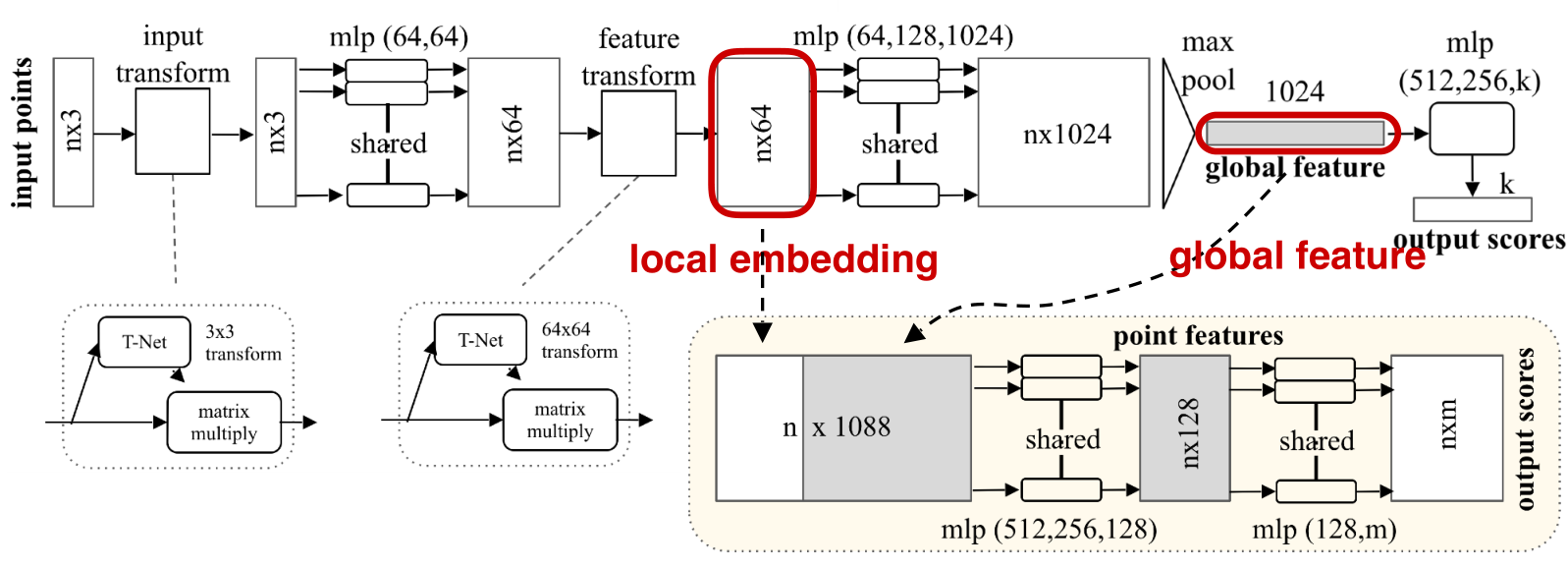
- 在目标分割时,全局特征已经不具有每个点的信息了,所以与maxpool前的数据进行了特征的拼接,再经过MLP,得到每个点的分类得分。
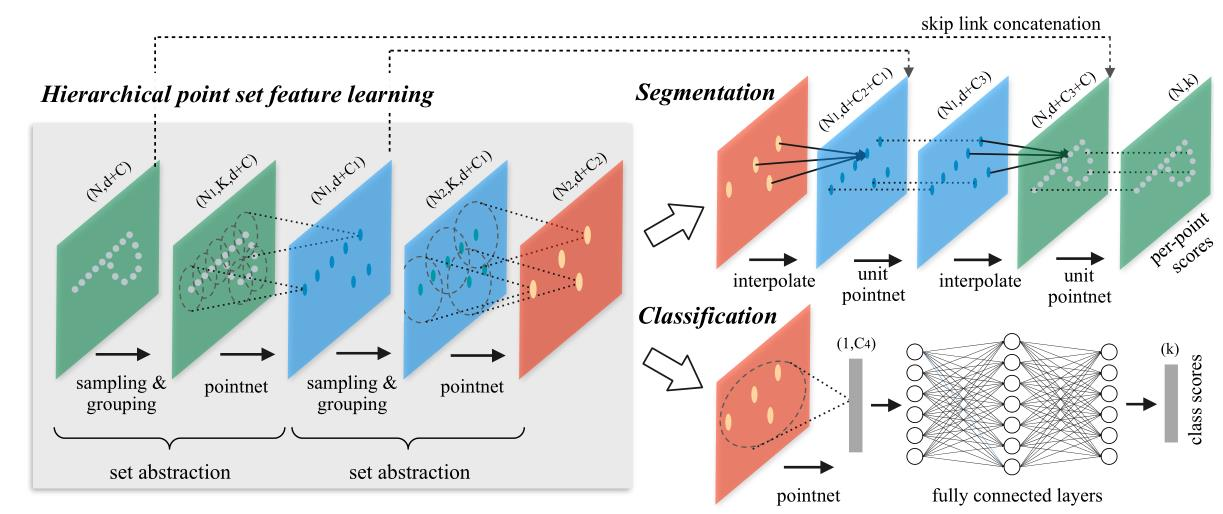
PointNet++
- PointNet++2017,PointNet没有局部区域的关注,PointNet++借鉴了CNN的思想,通过串联的多级别的感受野,多层次特征提取结构提升模型性能,同时保证旋转不变性和顺序无关性。
改进
- 整体流程:
- sampling centroid抽样:在点云中首先通过centroid中心点
- group points by centroid组类别选取:在centroid周围的点组成一个组,多个centroid将点集划分为重叠的局部区域。
- pointnet on each group:对每个组进行pointnet识别,此时通过多个局部信息的学习,模型就具有了上下文的信息了
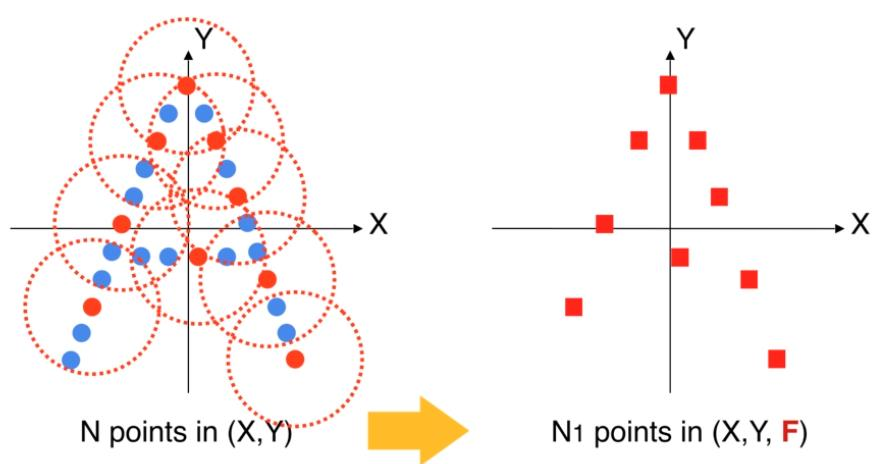
- 与CNN相似,提取局部特征以捕获来自小邻域的精细几何结构。这些局部特征将进一步分组为较大的单元,并进行处理以生成更高级别的特征。重复此过程,直到获得整个点集的特征为止。
结构图
采样的方法
- uniform sampling:均匀采样
- farthest sampling:最远点采样,可以更好的覆盖采样空间。类似于kmeans++初始点选取
input points, we use iterative FPS to choose a subset of points, such that is the most distant point(in metric distance) from the set with regard to the rest points.
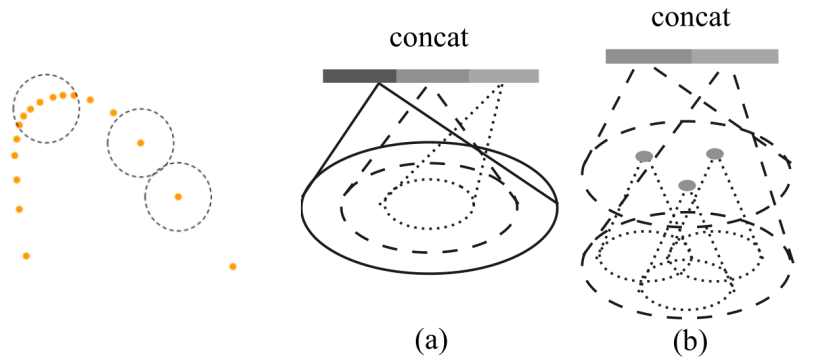
分组方法
- K nearest neighbors:KNN算法
- Ball query:球查询的方法
- 查找点求半径范围所有点,可以保证固定区域尺寸,是区域特征更具通用性
插值方法
- 在分割时,由于点云的稀疏,需要进行Feature Porpagation进行插值,插值方法基于距离权重的倒数平均,基于KNN(p=2,k=3)
非均匀点云数据优化
- 由于点云数据的近密远疏,噪声的非均匀点云对于PointNet非层次话的学习有很大的影响,PointNet使用MRG方法,增加多尺度信息
- Multi-scale grouping(MSG):多尺度的拼接,拼接多个视野的特征点,数量级较大
- Multi-resolution grouping(MRG):多层次的凭借,分层拼接
- Single scale grouping (SSG)
MV3D
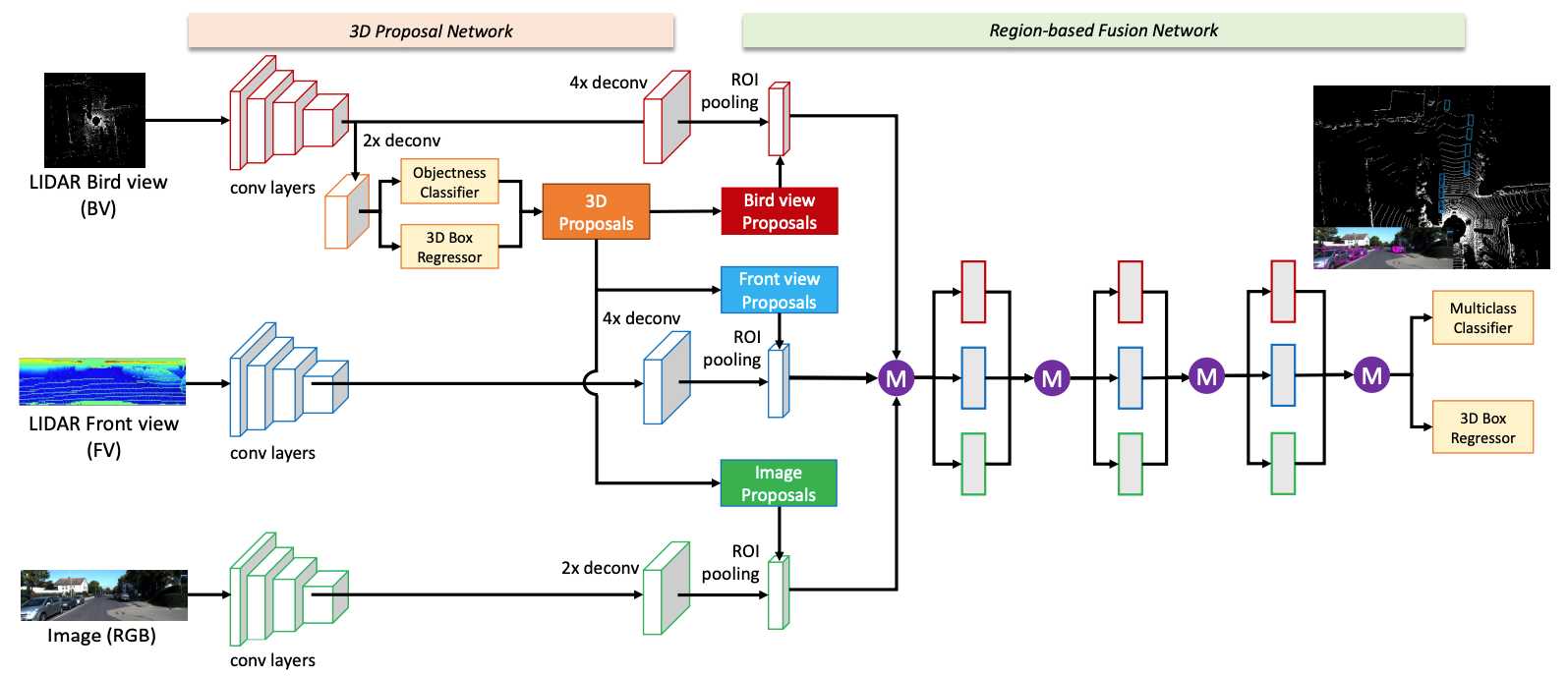
- 将点云投影到两个方向(brid view+front view) + Faster RCNN
• 3D proposal from BV, project into other views
• ROI pooling in each view, combined for Cls./Reg. - Pioneer work but not frequently used nowadays
VoxelNet
- VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection, Yin Zhou, et.al.
步骤
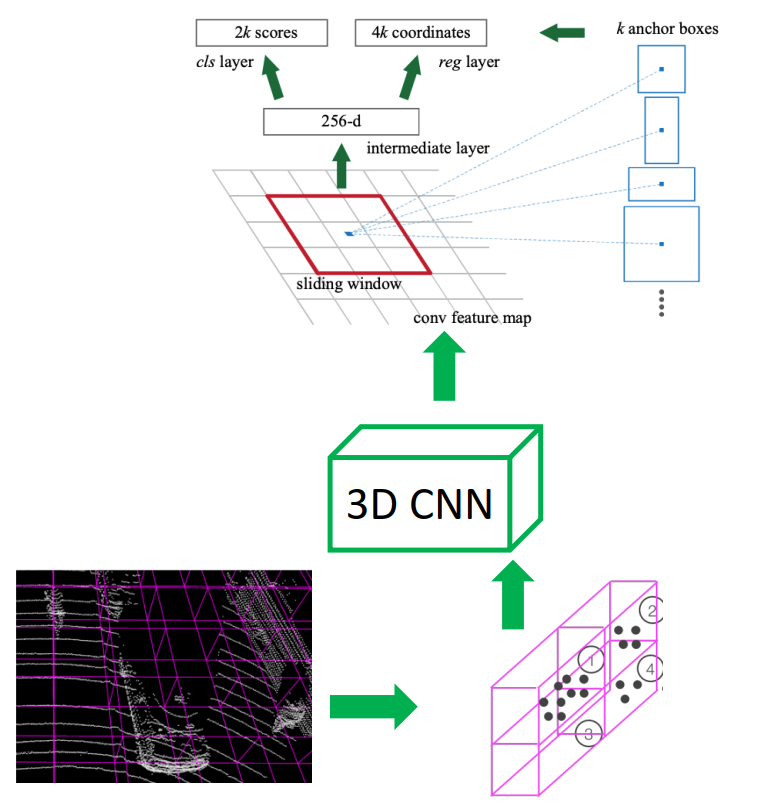
- Build voxel grid
- Get feature per-cell:PointNet
- 3D voxel → 2D feature map: 3D convolution
- Region Proposal Network (RPN)
- One network for one category.
- RPN is only predicting if the anchor box is an object
流程
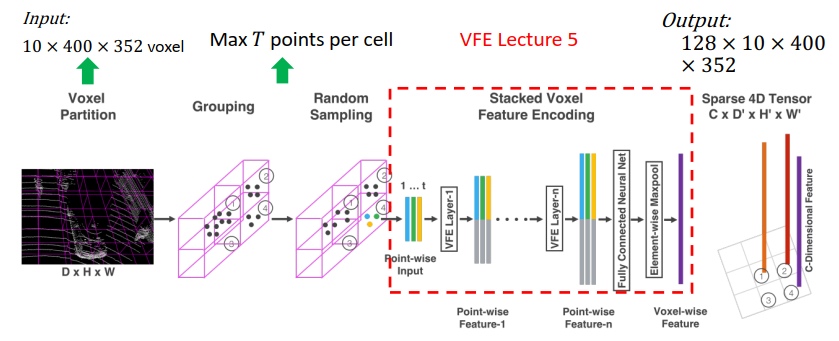
- 由于点云比较稀疏,90%的voxel都是空的,造成计算的浪费,作者对100x400x352体素的表达进行了定义
- Build two containers
- K – maximum number of non-empty voxels
- T – maximum number of points per voxel
- 𝐾 × 𝑇 × 7 for points:(𝑥𝑖, 𝑦𝑖, 𝑧𝑖, 𝑟𝑖, 𝑥𝑖 − 𝑣𝑖𝑥, 𝑦𝑖 − 𝑣𝑖𝑦, 𝑧 − 𝑣𝑖𝑧)
- 𝐾 × 3 for voxel coordinates
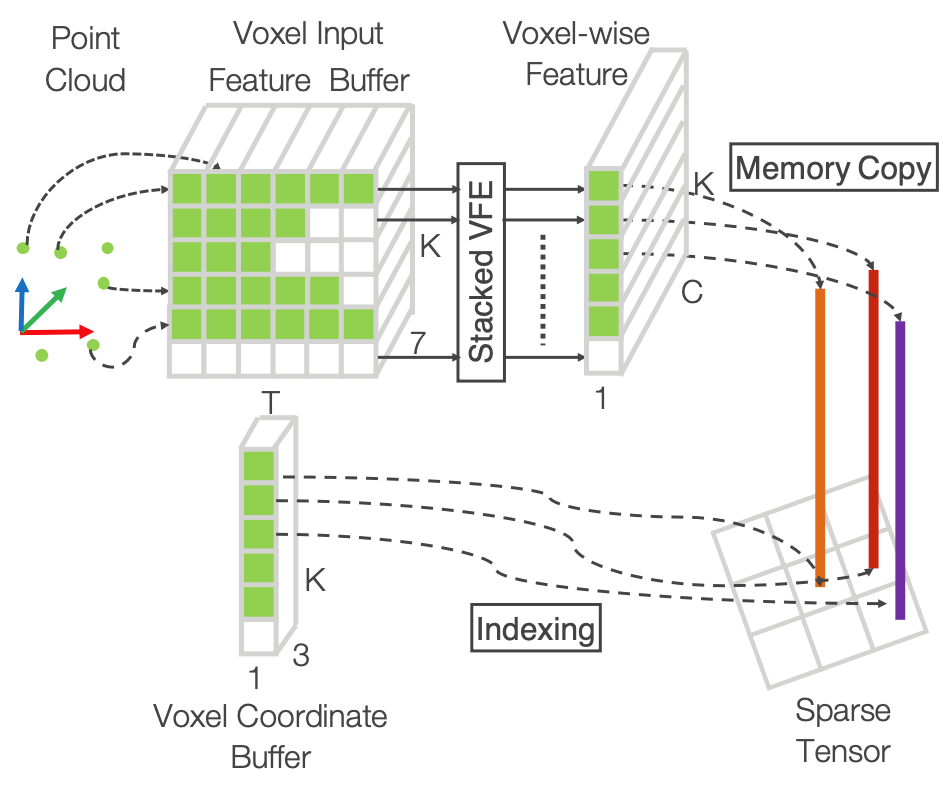
- Iterate each point
- Determine voxel coordinate (ℎ𝑥, ℎ𝑦, ℎ𝑧):Hash(ℎ𝑥, ℎ𝑦, ℎ𝑧) → index 𝑘 in container ©(d)
- If 𝑘-th element exist in ©/(d), append to ©
- If not, create 𝑘-th element in © (d)
- VFE / PointNet on © → 𝐾 × 128
- Put © back to the voxel grid → 128 × 10 × 400 × 352
- Input: 128 × 10 × 400 × 352 → Conv3D
- Output channel # 64, kernel (3, 3, 3), stride (2, 1, 1), padding (1, 1, 1)
- Output channel # 64, kernel (3, 3, 3), stride (1, 1, 1), padding (0, 1, 1)
- Output channel # 64, kernel (3, 3, 3), stride (2, 1, 1), padding (1, 1, 1)
- Output: C′ × 𝐷′ × 𝐻′ × 𝑊′ → 64 × 2 × 400 × 352
- Reshape into 2D feature map 2𝐶′ × 𝐻′ × 𝑊′
- This is image-like feature map!
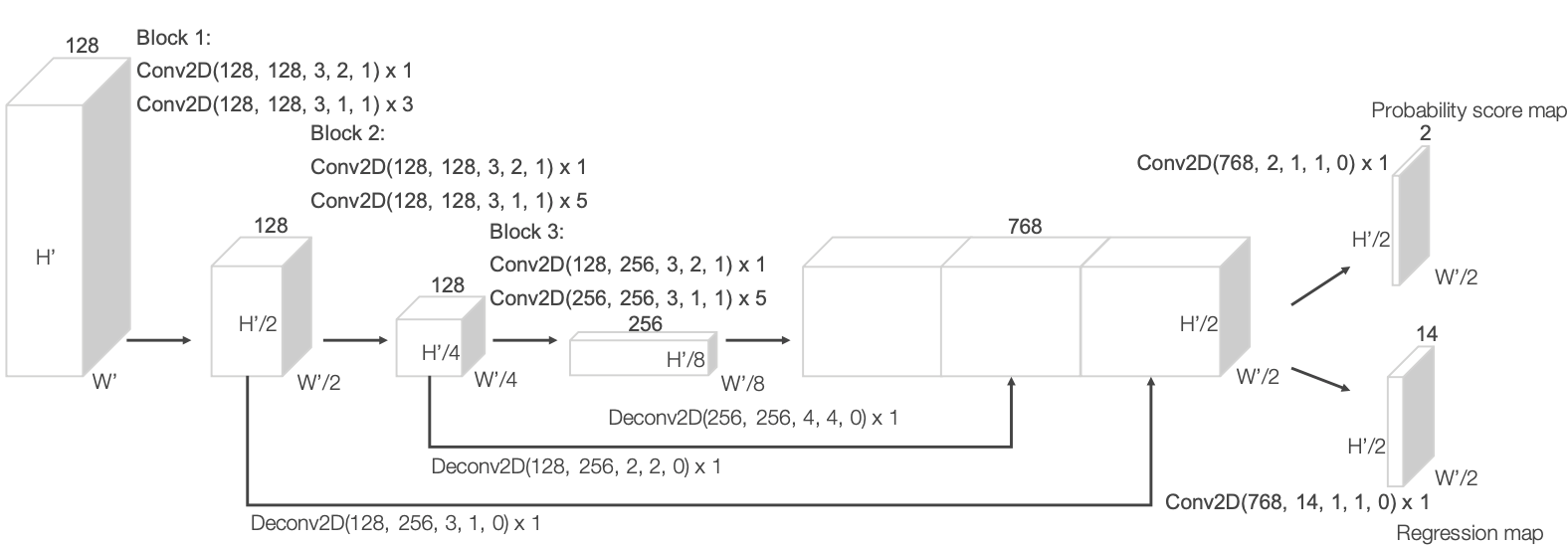
- 再经过分类网络和回归网络得到分类和位置
损失
-
- is “Binary Cross Entropy Loss” – in fact not a standard one
- VoxelNet represents the ”objectness confidence” with only 1 number, instead of 2.
-
Ground truth box:
-
A matching anchor box (positive box):
-
Loss between Ground truth and positive anchor box:
- 其中:
PointPillars
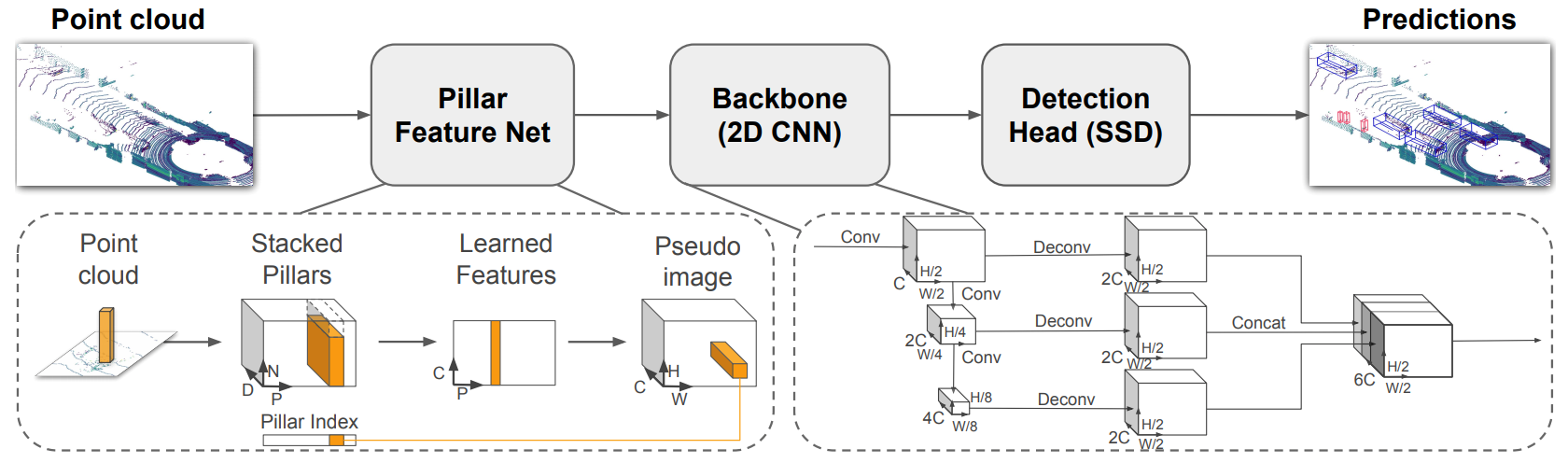
损失函数
-
- 其中:same as VoxelNet,except:
- ,这里的角度在某些特定值无效
- :将旋转划分为090,90180,180270,270360
- :使用focalloss代替crossentropyLoss,解决类别不均衡问题
- 其中:same as VoxelNet,except:
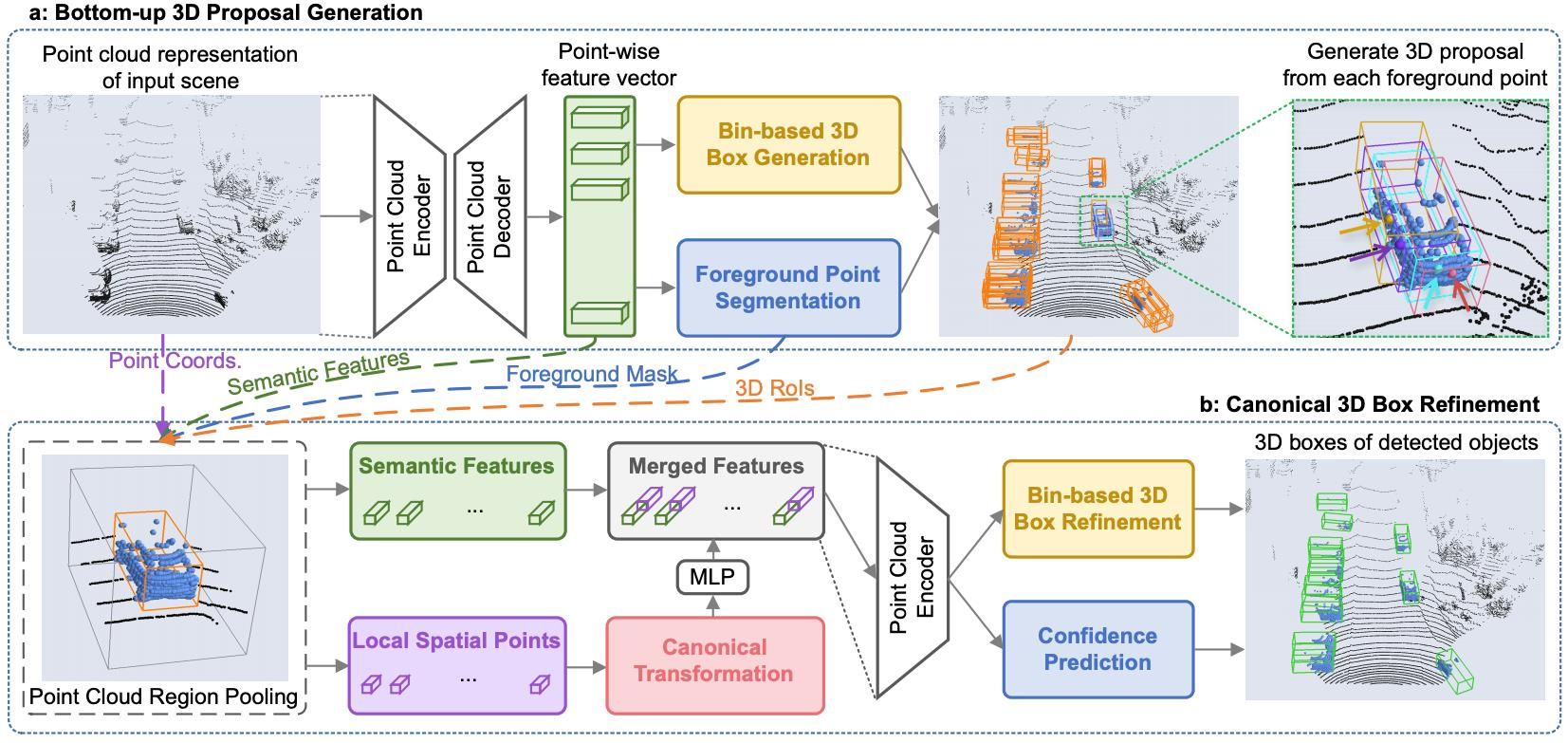
PointRCNN
Frustum PointNet
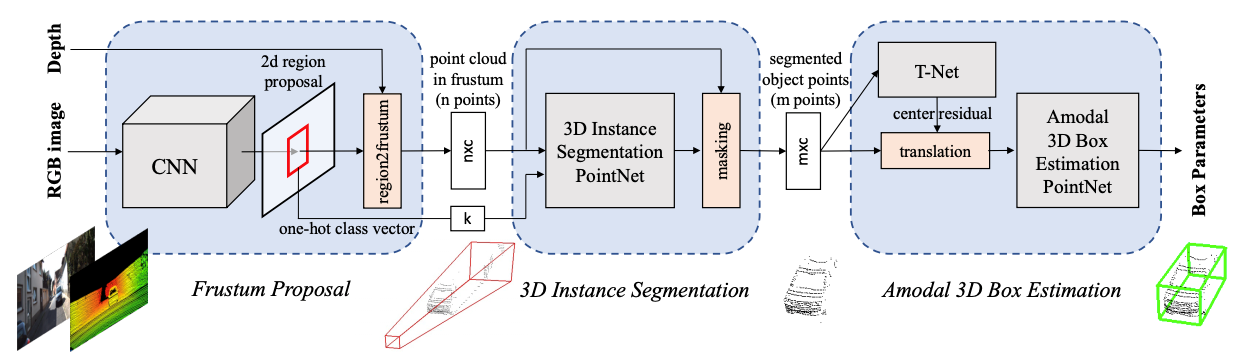
- 用MaskRCNN将图像中的目标进行分割,再映射到三维点云中的数据,得到分割的实例
- 实际效果取决于MaskRCNN,而其基于二维,丢失了很多信息
- 点云数据和图像数据不一定是同步的,可能有延迟以及视差,导致工程场景并不十分精确
PointPainting
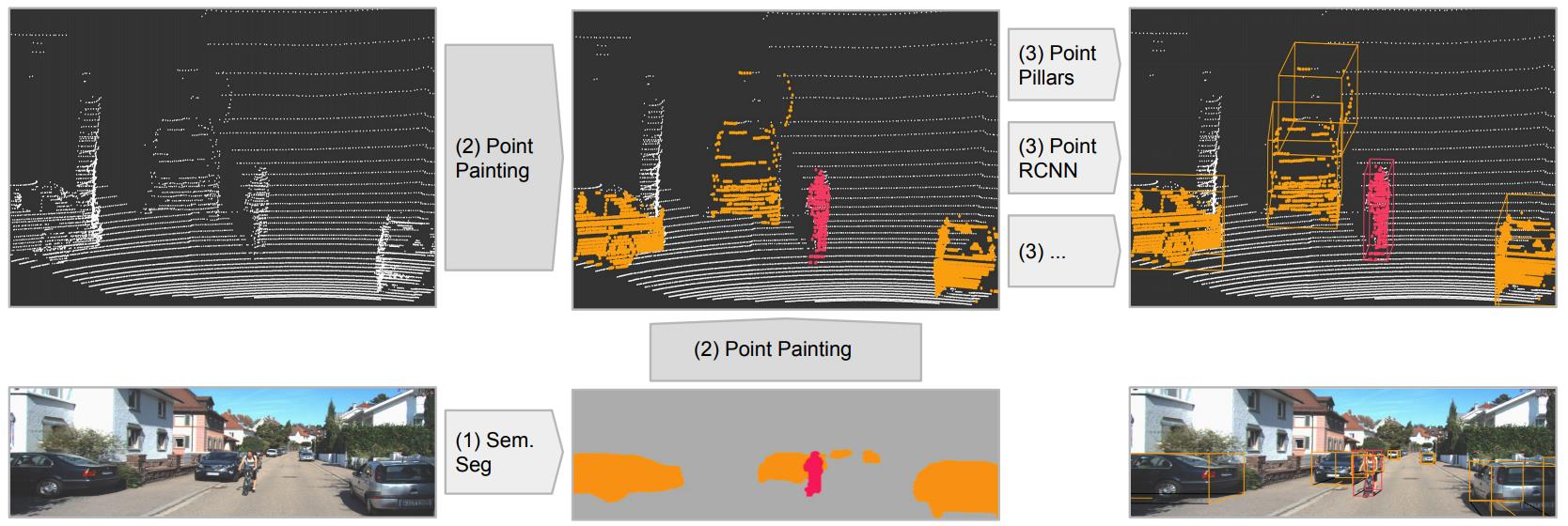
- Augment each point with the semantic segmentation label from an image based semantic segmentation network.
SoNet
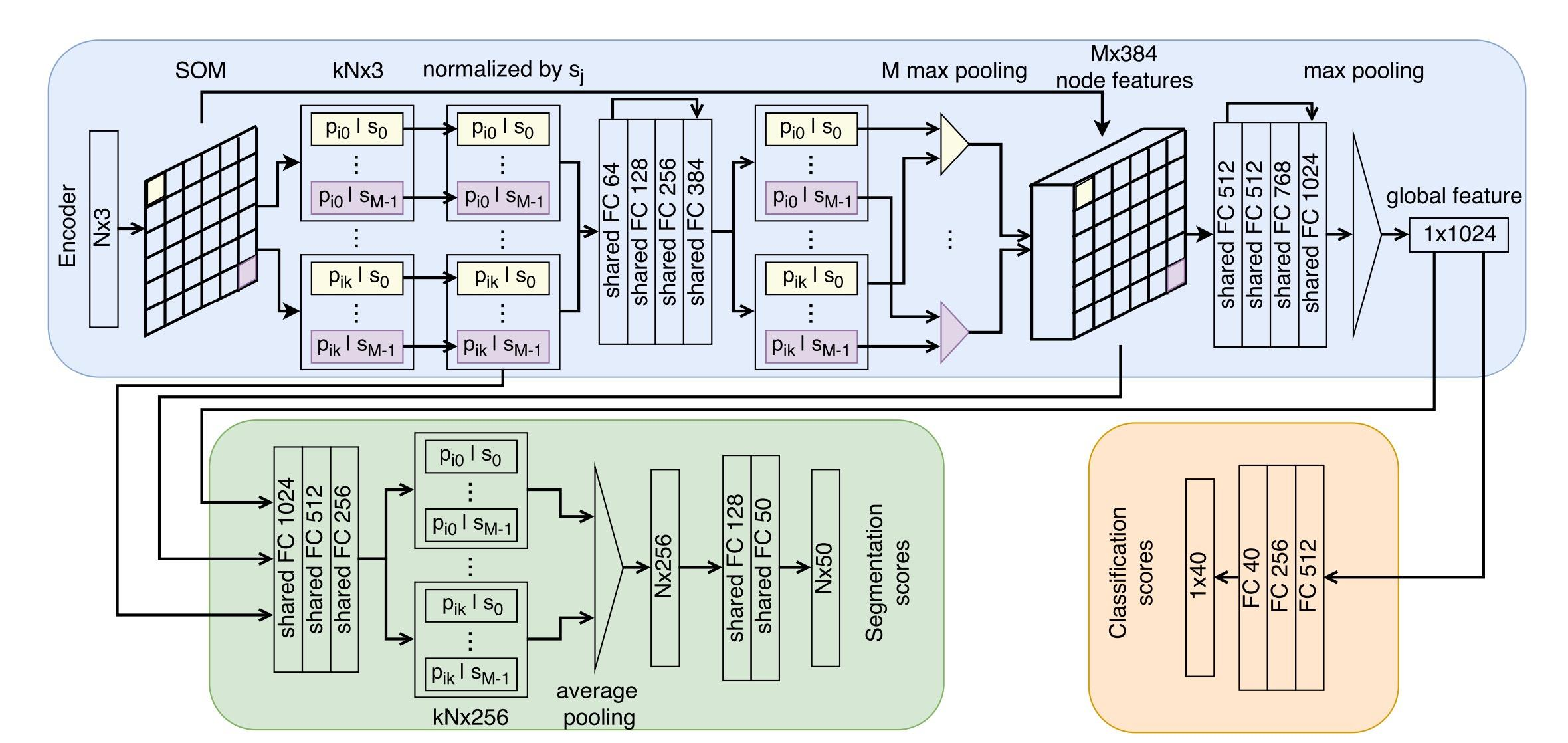
- 自组织映射
- point to node