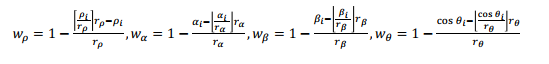降维

谱定理spectral theorem

• 谱定理是线性代数中很重要很基础的定理，并为以后的特征值分解做准备
• 谱定理：设A是nxn满秩对称矩阵，存在正交向量u，$Au_i=\lambda_iu_i$，满足下面的等式：
  • $A=U\Lambda U^T=\sum_{i=1}^{n}\lambda_iu_iu_i^T,\;\Lambda=diag(\lambda_1,\cdots,\lambda_n)$
  • 其中：$UU^T=U^TU=I$

瑞利商

• Rayleigh Quotient定义函数为瑞丽商
  • $R(A,x)=\frac{x^HAx}{x^Hx}$
  • 其中x为非零向量，而A为n×n的Hermitan矩阵。所谓的Hermitan矩阵就是满足共轭转置矩阵和自己相等的矩阵，即$A^H=A$。如果我们的矩阵A是实矩阵，则满足$A^T=A$的矩阵即为Hermitan矩阵。
• 瑞利商$R(A,x)$有一个非常重要的性质，即它的最大值等于矩阵A最大的特征值，而最小值等于矩阵A的最小的特征值，也就是满足
  • $\lambda_{min}\le\frac{x^HAx}{x^Hx}\le\lambda_{max},\;\forall x\ne0$
  • $\lambda_{max}(A)=\max_{x:||x||_2=1}x^TAx$
  • $\lambda_{min}(A)=\min_{x:||x||_2=1}x^TAx$
  • 解释瑞丽商就是：经过x和xT旋转变换后的最大最小值是多少，旋转不会改变特征值的大小
• 当向量x是标准正交基时，即满足$x^Hx=1$时，瑞利商退化为：$R(A,x)=x^HAx$，这个形式在谱聚类和PCA中都有出现。

SVD

• 有一个m×n的实数矩阵A，我们想要把它分解成如下的形式:

  • $A=U\Sigma V^T$
  • 其中U和V均为单位正交阵，即有$UU^T=I$和$VV^T=I$，U称为左奇异矩阵，V称为右奇异矩阵，Σ仅在主对角线上有值，我们称它为奇异值，其它元素均为0。上面矩阵的维度分别为$U\in R^{m×m}$, $Σ\in R^{m×n}$, $V\in R^{n×n}$。

• 一般地Σ有如下形式

  • $\Sigma=\begin{bmatrix}\sigma_1&0&0&0&0&0\\0&\sigma_2&0&0&0&0\\0&0&\cdots&0&0&0\\0&0&0&0&\cdots&0\end{bmatrix}_{m\times n}$

• 正常求上面的U,V,Σ不便于求，我们可以利用如下性质:

  • $AA^T=U\Sigma V^TV\Sigma^TU^T=U\Sigma \Sigma^TU^T$（2-2）
  • $A^TA=V\Sigma^TU^TU\Sigma V^T=V\Sigma^T\Sigma V^T$（2-3）
  • 注：需要指出的是，这里$\Sigma\Sigma^T$与$\Sigma^T\Sigma$在矩阵的角度上来讲，它们是不相等的，因为它们的维数不同$\Sigma\Sigma^T\in R_{m\times m}$，而$\Sigma^T\Sigma\in R_{n\times n}$，但是它们在主对角线的奇异值是相等的
  • $\Sigma\Sigma^T=\begin{bmatrix}\sigma_1&0&0&0\\0&\sigma_2&0&0\\0&0&\cdots&0\\0&0&0&\cdots\end{bmatrix}_{m\times m}$，$\Sigma^T\Sigma=\begin{bmatrix}\sigma_1&0&0&0\\0&\sigma_2&0&0\\0&0&\cdots&0\\0&0&0&\cdots\end{bmatrix}_{n\times n}$

• 可以发现$AA^T$和$A^TA$也是对称矩阵，那么可以利用式（1-1），做特征值分解。利用式（2-2）特征值分解，得到的特征矩阵即为U；利用式（2-3）特征值分解，得到的特征矩阵即为V；对$\Sigma\Sigma^T$或$\Sigma^T\Sigma$中的特征值开方，可以得到所有的奇异值。

PCA & Kernel PCA

Kernel PCA可以理解为，先通过非线性变换，将点云投影到高维空间中，然后在高维空间中做PCA。但这个非线性变换函数很难找，所以通过数学变换，改写，用核方法表示。使用常用的，多项式的核，高斯的核就可以实现Kernel PCA。

PCA步骤

• 输入：$x\in\mathbb{R}^n,\;i=1,2,\cdots,m$
• 输出：最主要的特征向量$z_1,z_2,\cdots,z_k\in\mathbb{R},k\le n$
• 将数据归一化
  • $\tilde{X}=[\tilde{x_1},\cdots,\tilde{x_m}]$
  • 其中：$\tilde{x_i}=x_i-\bar{x},\;i=1,\cdots,m$
  • $\bar{x}=\frac{1}{m}\sum_{i=1}^{m}x_i$
• 计算得到最大的方差时的投影方向z，$z\in\mathbb{R}^n,\left\|z\right\|_2=1$
  • 投影：$a_i=\tilde{x}_i^Tz$
• 计算投影的方差，由于数据中心化，方差为数据的平方和
  • $\frac{1}{m}\sum_{i=1}^{m}a_i^2=\frac{1}{m}\sum_{i=1}^{m}z^T\tilde{x}_i\tilde{x}_i^Tz=\frac{1}{m}z^T\tilde{X}\tilde{X}^Tz$
• 转化为求最值的问题：
  • $\max_{z\in\mathbb{R}^n}z^T(\tilde{X}\tilde{X}^T)z,\;s.t.\left\|z\right\|_2=1$
• 根据瑞丽熵：
  • $\lambda_{min}(A)\le\frac{x^TAx}{x^Tx}\le\lambda_{max}(A),\forall{x}\ne{0}$
• 谱定理：
  • $A=U\Lambda U^T=\sum_{i=1}^{n}\lambda_iu_iu_i^T,\Lambda=diag(\lambda_1,\cdots,\lambda_n)$
• 最值问题可以转为求解特征值特征向量
  • $H=\tilde{X}\tilde{X}^T=U_r\Sigma^2U_r^T$

Kernel PCA

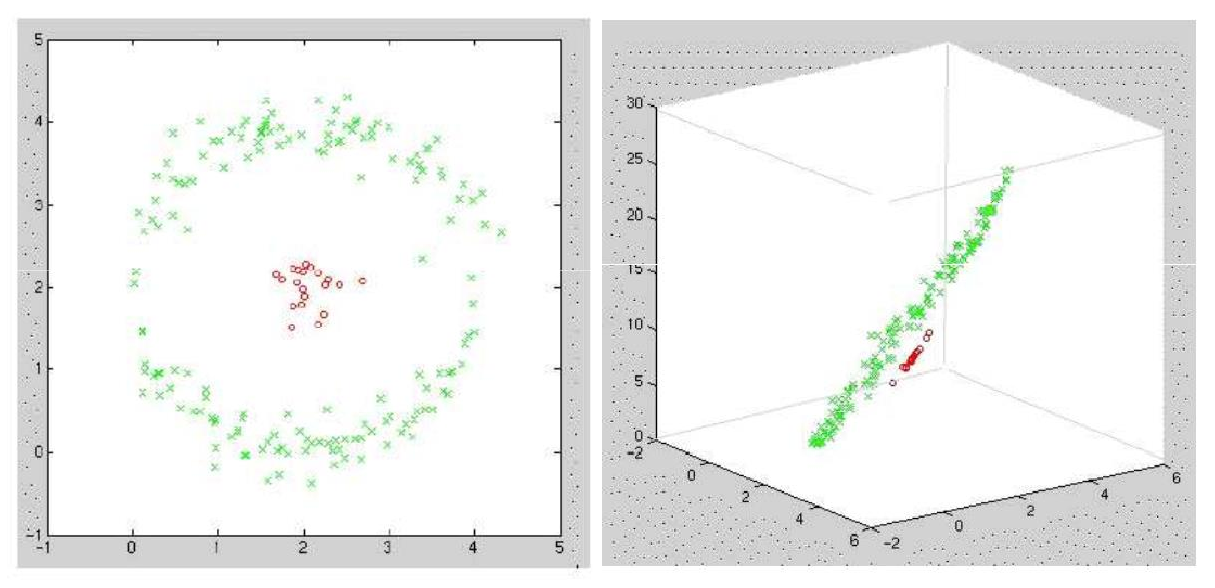
• 例如原始数据为两组，一组是二维的圆上的数据，一组为圆心周围的数据，数学表达为：$x_i=[x_{i1},x_{i2}]\in\mathbb{R}^2$
• 增加一个维度，就是数据相对原点的距离：$x_i=[x_{i1},x_{i2},x_{i1}^2+x_{i2}^2]\in\mathbb{R}^3$
• 此时变为三维空间后，就可以很好的分类两组数据

核函数	公式
Linear	$k(x_i,x_j)=x_i^Tx_j$
Polynomial	$k(x_i,x_j)=(1+x_i^Tx_j)^p$
Gaussian	$k(x_i,x_j)=e^{-\beta\left\|x_i-x_j\right\|_2}$
Laplacian	$k(x_i,x_j)=e^{-\beta\left\|x_i-x_j\right\|_1}$

法向量估计

• Surface Normal就是PCA中中最后一维的向量(也就是方差最小的向量z)，将点云做PCA，最后一个主成分就是法向量的方向，curvature也与PCA中最小的特征值有关。

法向量计算步骤

• 选取一个点
• 寻找周围的邻居点
• 将这些点通过PCA计算最不显著的向量
• 曲率为最小特征值比上所有特征值之和

  $curvature=\frac{\lambda_n}{\sum_{i=1}^{n}\lambda_i}$

滤波

去噪

Radius Outlier Removal

• 在每个点计算半径r内是否相邻指定的点，不包含则丢弃

Statistical Outlier Removal

• 计算所有点半径r内每个邻居的距离的平均值和方差，再对每个点计算邻居，大于$3\sigma$则认为是噪声

下采样

Voxel Grid Downsampling

• pcl库中使用排序的方法，时间时间复杂度是O(NlogN)，如果使用哈希表，其实感觉就像是桶排序，可以做到O(N)
• 分成指定网格，再在网格中取一个点代表这个网格，选择方法：平均值、随机点

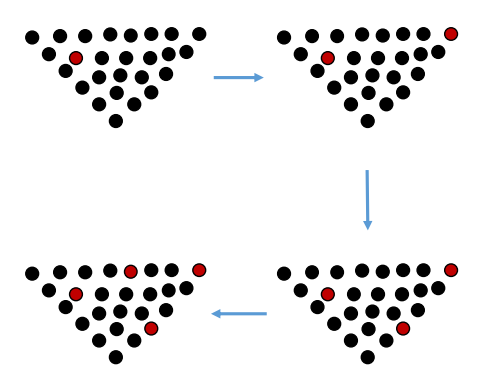
FPS

• Farthest Point Sampling，可以将比较密集的点去除
• Randomly choose a point to be the first FPS point
• Iterate until we get the desired number of points
• For each point in the original point cloud, compute its distance to the nearest FPS point
• Choose the point with the largest value, add to FPS set

Normal Space Sampling

• 在曲率大的地方多采样

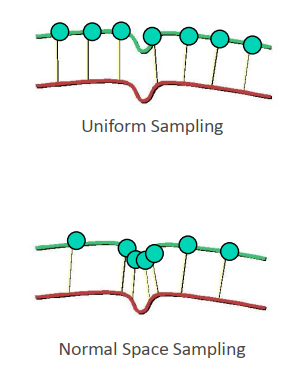
DeepLearning：《learning to sample》

• 语义上进行降采样

上采样

Bilateral Filter – Gaussian Filter

• 对像素值与周围进行平均，可以对图像进行平滑，但是会将边缘丢失。
  • 高斯核：$G_\sigma(x)=\frac{1}{2\pi\sigma^2}exp(-\frac{x^2}{2\sigma^2})$
• Bilateral Filter使用了两个高斯核，当是边缘时，权重会比较小
  • $BF[I]_p=\frac{1}{W_p}\sum_{q\in S}G_{\sigma_s}(\left\|p-q\right\|)G_{\sigma_r}(I_p-I_q)I_q$
  • 其中：$W_p=\sum_{q\in S}G_{\sigma_s}(\left\|p-q\right\|)G_{\sigma_r}(I_p-I_q)$

最近邻Nearset Neighbor Problem

Binary Search Tree

• 处理1维问题

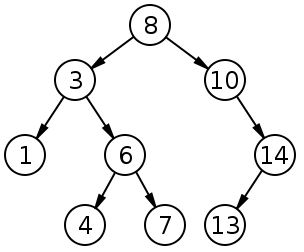
KD-Tree

• KD-Tree：k-dimensional tree，高维度的二叉树，每个维度切一刀

• 切法：

  1. 轮流切，xyzxyz
  2. adaptive，按照点的分布切

• 两种速度差别并不是很大，结果是一样的。

• 构建速度，最快O(nlogn)，使用O(n)的求中值的方法，但很复杂。有以下两个trick：

  1. 找中值时，不用某个区域的全部点，而是只用一部分
  2. 用平均值代替中值

• 这两个trick生成的树不是平衡树，但用起来还算可以

• 查找时需要根据worst-distance判断查找范围

Octree

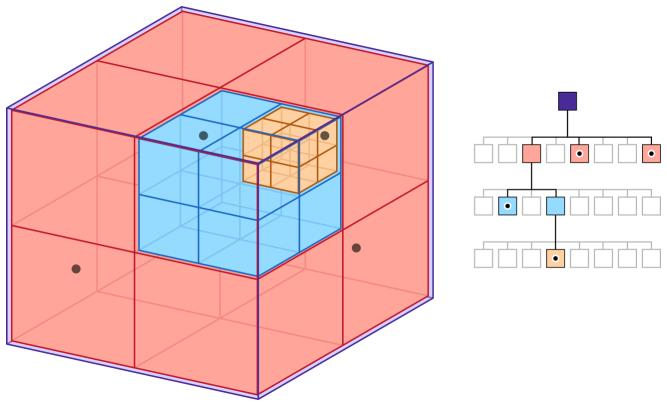
• 专门为三维数据设计的，在最近点搜索中比较高效的原因是，可以提前终止搜索。使用KD-Tree，无论如何都会返回到root。
• 构建八叉树的时候，要确定leaf_size和最小边长。

聚类

k-means

步骤

• 𝑁 input data points, find 𝐾 clusters.
• 输入：𝑥1, ⋯ , 𝑥𝑁 , 𝑥𝑛 ∈ ℝ𝐷
  1. Randomly select K center points
  2. Each data point is assigned to one of the K centers. Cluster center 𝜇𝑘, 𝑘 = 1, ⋯ 𝐾。
  • 𝜇𝑘 is the center of 𝑘𝑡ℎ cluster
  3. Re-compute the K centers by the mean of each group
  4. Iterate step 2 & 3. Objective of K-Means is to minimize the distortion measure:
  • $J=\sum_{n=1}^{N}\sum_{k=1}^{K}r_{nk}\left\|x_n-\mu_k\right\|^2$

Tricks

• 选择数据中的点作为初始化点，而不是随机选点
• 由于K-menas选点的初始值有关，所以跑几次K-menas，选择惩罚函数最小的一次作为结果
• Mini-Batch K-means
• Sequential K-means
• 欧氏距离不能用，就不能用K-menas，因为其要求平均值

k-medoids

• 对kmeans加强，为了增加对噪声的鲁棒性，不要求距离函数可导
• k中心点，将第i各类中的所有点，分别遍历其他所有点距离和最小的点作为类中心

GMM

高斯模型

• 一个变量的高斯模型：

  • $N(x|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}exp(-\frac{1}{2\sigma^2}(x-\mu)^2)}$

• 有D个维度的多维高斯

  • $N(x|\mu,\Sigma)=\frac{1}{(2\pi)^{\frac{D}{2}}}\frac{1}{|\Sigma|^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)^T)$

• K-means只给出中心点，不给出每个点的prob，还是比较粗糙的。使用GMM，每个类用一个高斯模型来拟合。

GMM

• 在现有x分布的状态下，类别z的概率分布：$p(z|x)=\frac{p(x|z)p(z)}{p(x)}$

  • 其中：$p(x)=\sum_{z}{p(z)p(x|z)}$
  • GMM是有向图，通过z来判断x：$p(x,z)=p(z)p(x|z)$
  • $p(z_i=1)=\pi_i$,$\pi\in[0,1],\sum_{i=1}^{K}\pi_i=1$
  • $p(z)=\prod_{i=1}^{K}\pi_i^{z_i}$

• GMM表达的K个高斯模型的线型组合，每个模型包含三个参数：

  • $p(x)=\sum_{k=1}^{K}\pi_kN(x|\mu_k,\Sigma_k)$
  • $\mu,\Sigma$高斯的参数
  • $\pi$高斯模型的权重

• 求解GMM时，也是用EM迭代优化得到GMM的参数

• K-means只是GMM的一个特例：GMM中每个高斯模型的方差都趋于0

K-means的优劣

• 优点：简单，快速
• 缺点：1）认为类别是各向同性的，2）需要预先确定K，3）易受初始化影响，4）对噪声铭感

EM

• EM不是特定于针对GMM的算法，而是针对求最大似然估计的方法，最大似然估计是要求
  $\max p(\theta|X)$。通过在$p(\theta|X)$引入预测的label，变成$p(\theta, Z|X)$。通过最大化来求取模型参数$\theta$。
  步骤
  1. 选择初始化的参数$\theta^{old}$
  2. E-step：估计$p(Z|X,\theta^{old})$
  3. M-step：根据优化问题，估计$\theta^{new}$
  • $\theta^{new}=\arg\max_\theta Q(\theta,\theta^{old})$
  • $Q(\theta,\theta^{old})=\sum_zp(Z|X,\theta^{old})\ln p(X,Z|\theta)=\mathbb{E}_z[\ln p(X,Z|\theta)]$
• 由于$P(\theta|X)$不好求，所以转为求上图中的Q，Q中的第一项就是给了模型估计点的label，很方便，第二项的求法是将$p(X, Z|X) = p(Z |\theta)p(X |Z,\theta)$，其中第一项是label的分布，在GMM中就是每个GM的权重，第二项是数据的先验分布。

Spectral Clustering

• 谱聚类先构建一个图，计算点与点之间的关系。用每个点与其他点的联系的权重组成的向量作为改点的vector。对所有点的vector进行压缩，然后使用压缩后的特征值进行k-menas。
• 不归一的谱聚类倾向于每个类中点的数量相似。
  1. Build the graph to get adjacency matrix 𝑊 ∈ ℝ𝑛×𝑛
  2. Compute unnormalized Laplacian 𝐿
  3. Compute the first (smallest) 𝑘 eigenvectors 𝑣1, ⋯ , 𝑣𝑘 of 𝐿
  4. Let 𝑉 ∈ ℝ𝑛×𝑘 be the matrix contraining the vectors 𝑣1,⋯ , 𝑣𝑘 as columns
  5. For 𝑖 = 1,⋯ 𝑛 , let 𝑦𝑖 ∈ ℝ𝑘 be the vector corresponding to the 𝑖-th row of 𝑉
  6. Cluster the points {𝑦𝑖 ∈ ℝ𝑘} with k-means algorithm into clusters 𝐶1,⋯ , 𝐶𝑘
  7. The final output clusters are 𝐴1, ⋯ ,𝐴𝑘 where 𝐴𝑖 = {𝑗|𝑦𝑗 ∈ 𝐶𝑖}
• 归一化的谱聚类倾向于每个类中点的密度相似。
  1. Build the graph to get adjacency matrix 𝑊 ∈ ℝ𝑛×𝑛
  2. Compute normalized Laplacian 𝐿′ = 𝐿𝑟𝑤
  3. Compute the first (smallest) 𝑘 eigenvectors 𝑣1, ⋯ , 𝑣𝑘 of 𝐿′
  4. Let 𝑉 ∈ ℝ𝑛×𝑘 be the matrix contraining the vectors 𝑣1,⋯ , 𝑣𝑘 as columns
  5. For 𝑖 = 1,⋯ 𝑛 , let 𝑦𝑖 ∈ ℝ𝑘 be the vector corresponding to the 𝑖-th row of 𝑉
  6. Cluster the points {𝑦𝑖 ∈ ℝ𝑘} with k-means algorithm into clusters 𝐶1,⋯ , 𝐶𝑘
  7. The final output clusters are 𝐴1, ⋯ ,𝐴𝑘 where 𝐴𝑖 = {𝑗|𝑦𝑗 ∈ 𝐶𝑖}

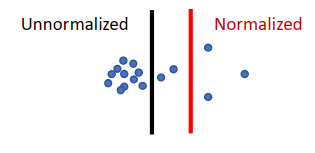
• 谱聚类可以自适应的选择类别的多少。
• 缺点：复杂，慢
• 优点：1）不对类的预先形状做假设，2）对任意维度的数据都可以处理，3）可以自动找出需要聚成多少个类

Mean Shift

Mean Shift步骤

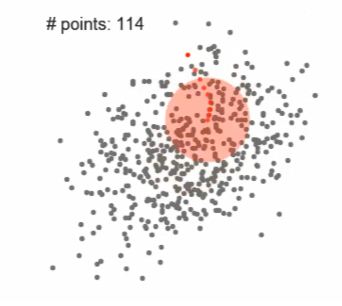
• 放置一个圆，计算圆的均值的位置，将圆的中心更新，继续计算直到稳定

做聚类的方法

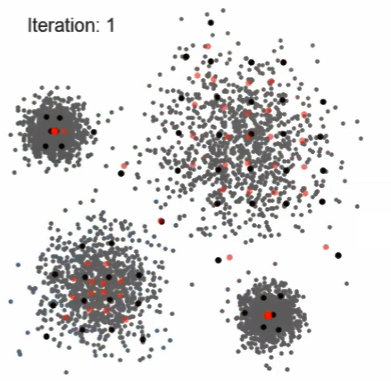
1. Randomly select a circle with radius 𝑟
2. Move the circle to the center of the points inside
3. Repeat step-2 until it doesn’t move
4. Repeat step-1,2,3. Remove overlapping circles

• If circles overlap, select the one with most points

5. Determine clusters by finding the nearest circle center (similar to k-means)

• Parameters: radius r

• 像爬山一样，最终散布的圆会聚集到k个比较密集的区域。以此将数据分为k个类

特点

• 不需要预先确定有多少个类
• 复杂度：O(Tnlgn)
• 还是认为类的分布是椭圆的，爬山也不一定爬到最优的中心
• 对高维稀疏的情况，设定R不易确定

DBSCAN

• Density-Based Spatial Clustering of Applications with Noise (DBSCAN)

步骤

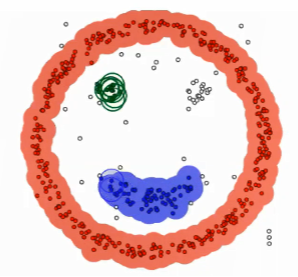
• Preparation: all points labeled as unvisited
• Parameters: distance 𝑟, min _samples
  1. Randomly select a unvisited point 𝑝, find its neighborhood within 𝑟
  2. Number of points within 𝑟 ≥ min _𝑠𝑎𝑚𝑝𝑙𝑒𝑠?
  • Yes. 𝑝 is a core point, Create a cluster 𝐶, go to step 3, mark 𝑝 as visited.
  • No. Mark 𝑝 as noise and visited.
  3. Go through points within its 𝑟-neighborhood, label it as 𝐶
  • If it is a core point, set it as the “new 𝑝”, repeat step-3
  4. Remove cluster 𝐶 from the database, go to step-1
  5. Terminate when all points are visited.

特点

• 同样不需要预先确定有多少类
• 与Spectral Clustering同为是考虑连接的，不假设类别是椭圆的。

模型拟合

最小二乘

• 拟合线性关系
  • $E=\sum_{i=1}^{n}(ax_i+by_i+c)^2$，求解abc，使得E最小
• 矩阵形式：
  • $\min E=\left\|Ax\right\|_2^2,s.t.\left\|x\right\|_2=1$
  • $A=\begin{bmatrix}x_1&y_1&1\\\vdots&\vdots&\vdots\\x_n&y_n&1\end{bmatrix}$
  • $x=[a,b,c]^T$
• 在A满秩的情况下，求解$x=(A^TA)^{-1}A^Tb$

噪声处理

• 2范数对噪声敏感，可以使用不同的优化函数，减小噪声的干扰

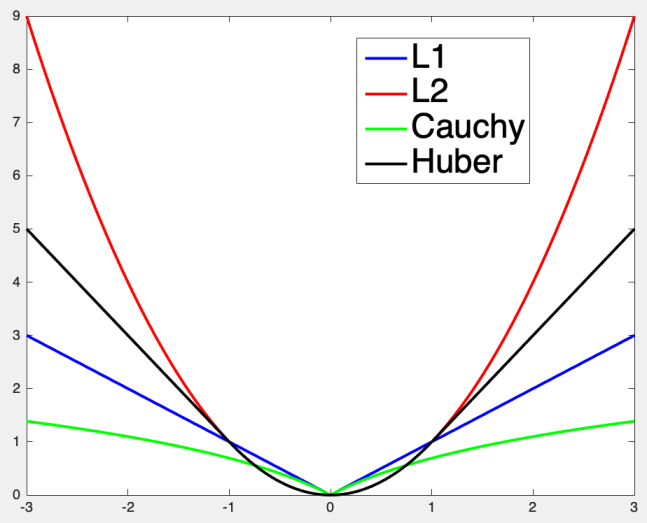
优化函数	公式
L1	$\rho=\|s\|$
L2	$\rho=s^2$
Cauchy	$\rho=\log(1+\|s\|)$
Huber	$\rho=\begin{cases}s^2,&\|s\|<\delta\\2\delta(\|s\|-\frac{1}{2}\delta),&otherwise\end{cases}$

• 使用了优化的损失函数，可以用梯度下降、高斯牛顿、LM方法求解最优解

Hough Transformation

• 使用极坐标表示直线，防止斜率k无穷大时无法表示的问题

  • $xcos\theta+ysin\theta=r$

• 对每个$\theta,r$进行计算x’,y’，与原始的x,y进行匹配，找到最合适的参数解

• 其他形状也同样使用

• 只适用于低维空间，否则计算量太大，一般要求模型参数<=3

RANSAC

步骤

1. 随机选择一个sample，用于表征模型所需的最小的点的个数

• $p_0,p_1$

2. 根据sample建立模型，计算a,b

• 𝑥 = 𝑥0 + 𝑎𝑡，𝑦 = 𝑦0 + 𝑏𝑡

3. 计算其余的点与模型的距离：

• 点到直线的距离：$d_i=\frac{n^T(p_i-p_0)}{\|n\|_2}$
• n表示法线向量

4. 计算某个接收区间的点的个数：

• $d_i<\tau$

5. 重复n次，找到接收最多的参数模型

$\tau$的设定

• $\tau$的设定可以由实验获得，但使用$\chi^2$分布并不靠谱，一般用经验确$\tau$的值。

• 假设点到模型的距离符合高斯分布，$d\sim N(0,\delta^2)$

• $\chi^2$分布：k个标准正态分布的和，假设在95%置信区间内满足点在区域内，则：

  • 1维：$\tau=\sqrt{3.84\delta^2}$
  • 2维：$\tau=\sqrt{5.99\delta^2}$
  • 3维：$\tau=\sqrt{7.81\delta^2}$

N的设定

• 定义概率p，做N次sample，都在接受区间的概率，当p至少为0.99的时候的N，为最佳的N
  • $(1-(1-e)^s)^N=1-p$
  • 其中：e：拒绝点的ratio
  • s：sample的点的个数
  • N：迭代次数
  • p：置信度至少一次得到最近加sample的概率
  • 1-p：一次好的都拿不到
• 得到：
  • $N=\frac{\log(1-p)}{\log(1-(1-e)^s)}$

提取特征点

Harris 2D

• 寻找角点，使得选取框可以对物体的位置比较敏感

定义

• 给定图像I上一点(x,y)视野移动(u,v)时变化为：

  • $E(u,v)=\sum_{x,y\in\Omega}w(x,y)[I(x+u,y+v)-I(x,y)]^2$
  • 其中$w(x,y)$表示对x,y方向上的权重

• 

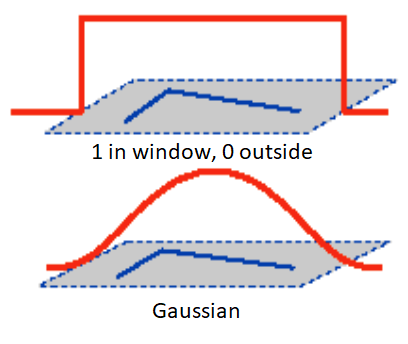
• u和v足够小时，上式可以等价于求导，使用一阶泰勒展开：

  • $f(x+u,y+v)\approx f(x,y)+uf_x(x,y)+vf_y(x,y)$

• 忽略w，令$w(x,y)=1$，使用一阶泰勒近似，上式可简化为：

  • $E(u,v)\approx \sum_{x,y\in\Omega}[I(x,y)+uI_x+vI_y-I(x,y)]^2=\sum_{x,y\in\Omega}u^2I_x^2+2uvI_xI_y+v^2I_y^2$
  • $=\sum_{x,y\in\Omega}\begin{bmatrix}u&v\end{bmatrix}\begin{bmatrix}I_x^2&I_xI_y\\I_xI_y&I_y^2\end{bmatrix}\begin{bmatrix}u\\v\end{bmatrix}$

• 此时移动一个方块图像的变化可表示为：

  • $E(u,v)\approx\begin{bmatrix}u&v\end{bmatrix}M\begin{bmatrix}u\\v\end{bmatrix}$
  • M为协方差矩阵：$M=\sum_{x,y\in\Omega}\begin{bmatrix}I_x^2&I_xI_y\\I_xI_y&I_y^2\end{bmatrix}$

• 通过协方差矩阵的特征就可以判断是否是角点，因为其在x,y方向上都有较大的一阶导数变化
  

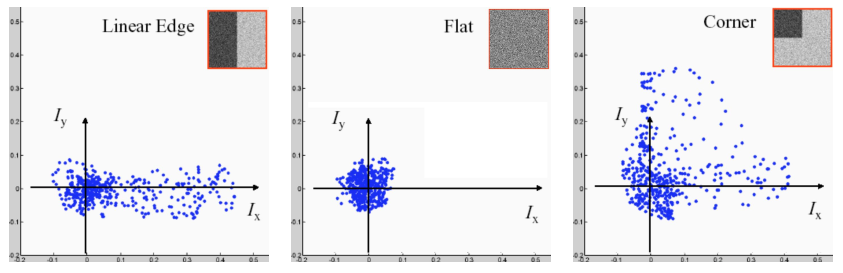
• 求M的特征值特征向量，令$R=min(\lambda_1,\lambda_2)$

Harris 3D&6D

数学表达

• 同理，对于3D空间的特征定义变换的方程

  • $E(u,v,w)=\sum_{x,y,z\in\Omega}[I(x+u,y+v,z+w)-I(x,y,z)]^2$
  • 一阶近似：$E(u,v,w)\approx\begin{bmatrix}u&v&w\end{bmatrix}M\begin{bmatrix}u\\v\\w\end{bmatrix}$
  • M为协方差矩阵：$M=\sum_{x,y,z\in\Omega}\begin{bmatrix}I_x^2&I_xI_y&I_xI_z\\I_xI_y&I_y^2&I_yI_z\\I_xI_z&I_yI_z&I_z^2\end{bmatrix}$

• 计算$I_xI_yI_z$的方法：

• 定义

  • p为要分析的点
  • 邻居域$\Omega$，包含点集：$x_i=[x_i,y_i,z_i]$
  • p的梯度向量$e=[e_x,e_y,e_z]^T\in\mathbb{R}^3$

• p点和其邻域的点的关系：

  • $(x_1-p_x)e_x+(y_1-p_y)e_y+(z_1-p_z)e_z=I(x_1,y_1,z_1)-I(p_x,p_y,p_z)$
  • 向量化：${x_i^T}'e=\triangle l_i$
  • $x_i'=[x_i',y_i',z_i']^T=[x_i-p_x,y_i-p_y,z_i-p_z]^T$]
  • $\triangle l_i=I(x_1,y_1,z_1)-I(p_x,p_y,p_z)$

• 多个邻域的点组合，得到矩阵

  • $Ae=b$
  • 当A满秩可逆，可得$e=(A^TA)^{-1}A^Tb$

• 得到e就可以得到每个方向上的一阶梯度，用以得到M矩阵

• 求M的特征值特征向量，令$R=\lambda_2$

e的优化

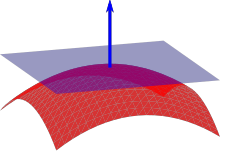
• 对于e，可以用一阶导数，也就是切面的梯度进行近似
• 根据邻域得到切平面：
  • $ax+by+cz+d=0$
  • 法向量：$n=\begin{bmatrix}n_x&n_y&n_z\end{bmatrix}=\frac{[a,b,c]^T}{\|[a,b,c]\|_2}$

距离的方法

• 对于雷达没有intensity时，无法获得b，此时，根据某个平面的距离作为b
• 要计算的p的切面法向量为n，对p做(u,v,w)移动后，相对切面变化的距离作为b
• 其M的表示为：
  • $M=\sum_{x,y,z\in\Omega}\begin{bmatrix}n_x^2&n_xn_y&n_xn_z\\n_xn_y&n_y^2&n_yn_z\\n_xn_z&n_yn_z&n_z^2\end{bmatrix}$
• 求M的特征值特征向量，令$R=\lambda_3$

6d

• 协方差矩阵$\begin{bmatrix}I_x,I_y,I_z,n_x,n_y,n_z\end{bmatrix}$

• 求M的特征值特征向量，令$R=\lambda_4$

• Harris3D分为使用intensity的和使用距离的两种。

• 使用intensity的方式，求得的梯度，投影到局部平面更好

• Harris6D，把intensity和法向量结合起来

ISS（Intrinsic Shape Signatures）

• 在邻域内点分布变化很大的地方。就是把邻域内的点拿出来，求协方差矩阵，然后再做特征值分解，找最小的特征值。

步骤

1. 在r的范围内计算每个点的协方差矩阵
2. 点的权重

• $w_j=\frac{1}{\|\{p_k:\|p_k-p_j\|_2<r\}\|}$

3. 加权协方差

• $cov(p_i)=frac{\sum_{\|p_j-p_i\|_2<r}w_j(p_j-p_i)(p_j-p_i)^T}{\sum_{\|p_j-p_i\|_2<r}w_j}$

4. 得到特征值$\lambda_i^1,\lambda_i^2,\lambda_i^3$由大到小
5. 判断是否是特征点：

• $\frac{\lambda_i^2}{\lambda_i^1}<\gamma_{21}$,$\frac{\lambda_i^3}{\lambda_i^2}<\gamma_{32}$
• 平面的约束为：$\lambda_i^1=\lambda_i^2>\lambda_i^3$
• 直线：$\lambda_i^1>\lambda_i^2=\lambda_i^3$
• 要确保：$\lambda_i^1>\lambda_i^2>\lambda_i^3$

6. NMS最大值抑制，选取$\lambda_i^3$，最小特征值比较大

• 上面两种传统方法，对噪声不鲁棒

USIP

• 三维特征点提取

1. 一个物体提取的特征点，在任意角度看仍然是特征点
2. 特征点具有尺度不变性

描述子

• 两大类：
  • 直方图，在某个范围计数，丢失旋转信息：
    • PFH & FPFH

• 基于坐标的，对旋转不适应：
  • SHOT

• 深度学习方法：
  • 3DMatch & Perfect Match
  • Perfect Match
  • PPFNet & PPF-FoldNet

PFH & FPFH

• Point Feature Histogram，输入：点云及其法向量+特征点

  1. 对6DOF的变化保持不变性
  2. 使用法向量的变化描述一个邻域

• 计算特征点邻域中每对点的3个特征，把这三个特征作为一个向量，放到一个voxel中。得到一个BxBxB大小的特征，B是voxel每个分量的grid的山数量

步骤

• 在某个邻域内，两两组合

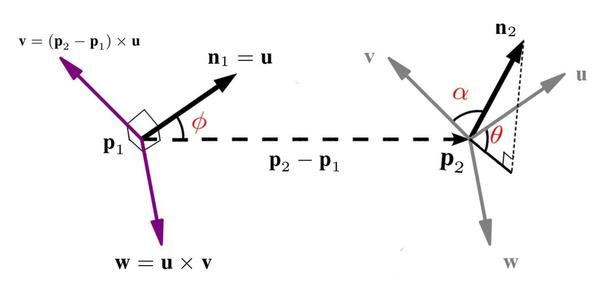
• 一对点p1和p2，其法向量分别为n1,n2，通过法向量和两点连线建立坐标系
  • $u=n_1$
  • $v=u\times \frac{p_2-p_1}{\|p_2-p_1\|_2}$
  • $w=u\times v$
• 四个特征：
  • $d=\|p_2-p_1\|_2$
  • $\alpha=v\cdot n_2$
  • $\phi=u\times \frac{p_2-p_1}{\|p_2-p_1\|_2}$
  • $\theta=\arctan(w\cdot n_2,u\cdot n_2)$
• 一般情况下，由于激光雷达数据近密远疏的性质，d的效果比较差，所以不做考虑，所以描述子可以表述为：
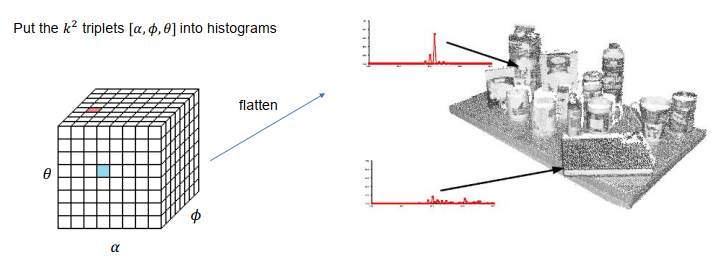
  • 在某个点的邻域内，有k个点，每对点的法向量的特征：$\alpha,\phi,\theta$，一共$k^2$个信息
• 以三维角度作为数据，每个角度有B个bin格子，建立$B^3$的立方体的直方图，将$k^2$的信息放入直方图
• 复杂度：$O(nk^2)$

• FPFH

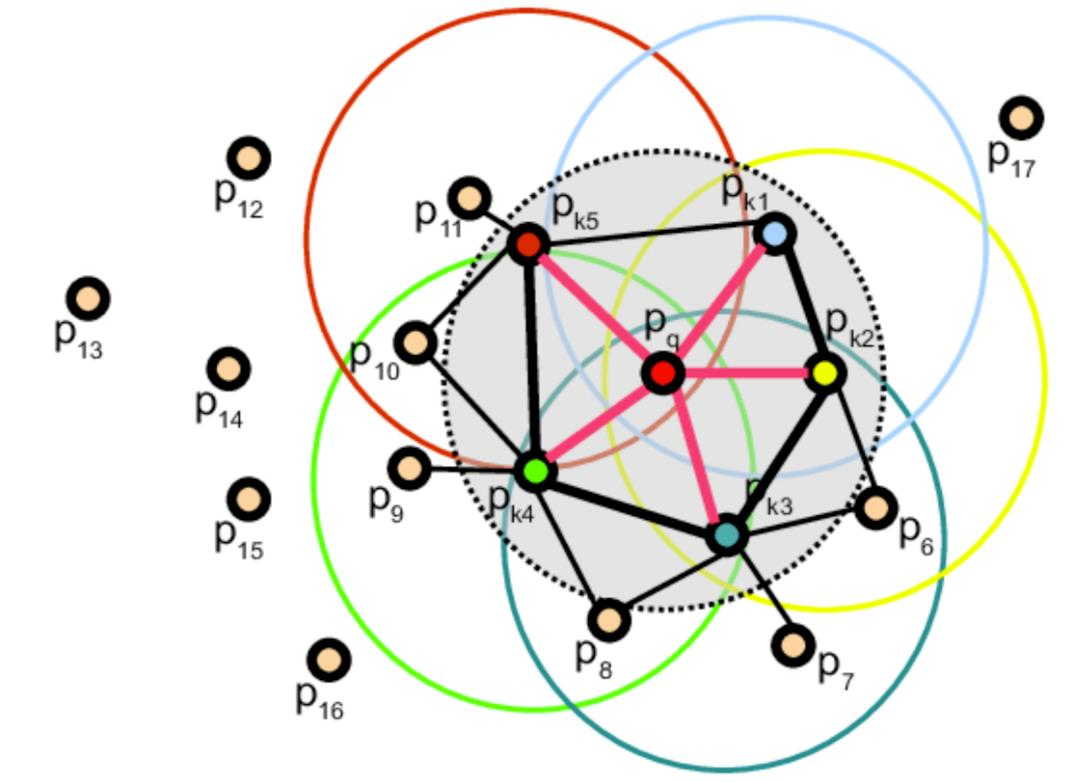
• 只对某个点和邻域的点组合，不再两两组合，同样得到三元组SPFH：$\alpha,\phi,\theta$

• 再与每个邻居的SPFH加权求和

  • $FPFH(p_q)=SPFH(p_q)+\frac{1}{k}\sum_{i=1}^{k}w_k\cdot SPFH(p_k)$
  • 其中：$w_k=\frac{1}{\|p_q-p_k\|_2}$

• 以每个角度为数据，B个bin格子，建立3个直方图，然后进行拼接，得到3B宽度的直方图

• 复杂度：$O(nk)$

• 直方图$3B$

SHOT

1. 使用加权的协方差矩阵做特征值分解，得到局部坐标系LRF

• $M=\frac{1}{\sum_{i:d_i\le R}(R-d_i)}\sum_{i:d_i\le R}(R-d_i)(p_i-p)(p_i-p)^T$
• 其中：$d_i=\|p_i-p\|_2$
• 计算三个特征向量作为坐标系：$x^+,y^+,z^+$，$x^-,y^-,z^-$
• 正负判断的标准是看哪边的点多：
• $S_x^+=\{i:d_i\le R\wedge(p_i-p)\cdot x^+\ge0\}$
• $S_x^-=\{i:d_i\le R\wedge(p_i-p)\cdot x^-\gt0\}$
• $x=\begin{cases}x^+,&\|S_x^+\|\ge\|S_x^-\|\\x^-,&otherwise\end{cases}$
• z轴通过叉乘求得

2. 按照这个局部坐标系把邻域分成一些小块
3. 用法向量来计算每个小块中直方图的特征
4. 使用插值实现软投票，解决boundary effect

• 软投票，避免因为噪声造成直方图偏差:

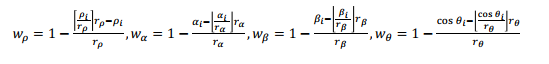
3DMatch

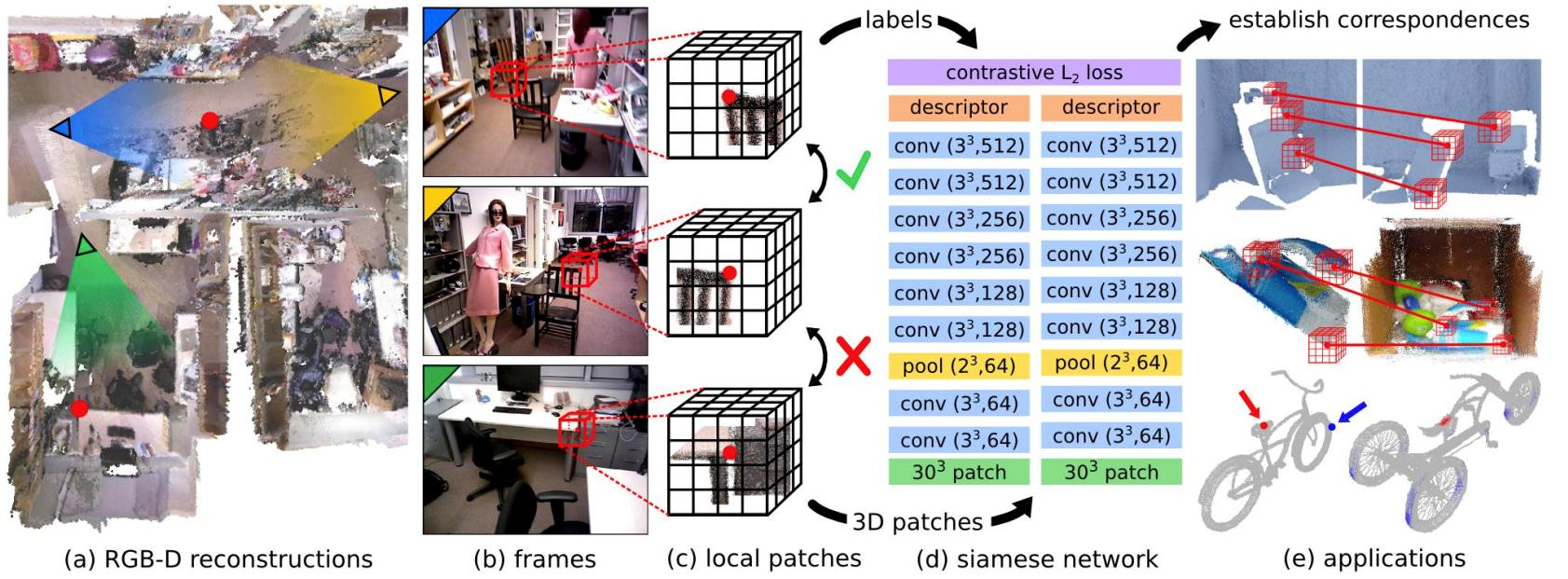
1. 在特征点周围建立局部的voxel，然后放到神经网络里面
2. 在不同视角下的相同点，做同样操作，得到positive的feature
3. 在不同点得到negative的feature
4. 用feature的距离代表相似程度
5. 使得negative的feature距离大，positive的feature距离近

• Contrastive Loss：$L=\frac{1}{N}\sum_{n=1}^{N}{y_{ij}d_{ij}^2+(1-y_{ij})max(\tau-d_{ij},0)^2}$，$d_{ij}=\|f(x_i)-f(x_j)\|_2$

局限

1. 对旋转过于敏感
2. loss约束过于强

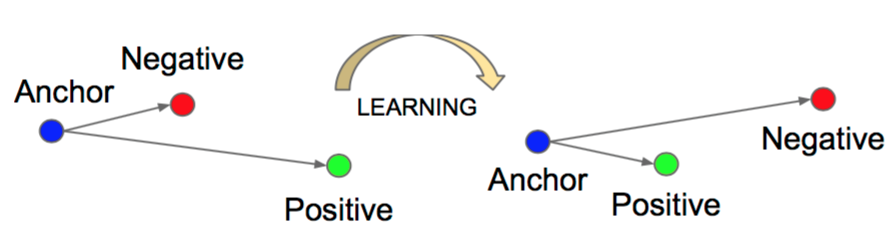
改进
1）建立局部坐标系，对于旋转是稳定的，然后在局部坐标系中简历voxel
2）使用 triplet loss，如何找到难度适中的三元组。

• $L=\sum_{i=1}^{N}max(d_i(a,p)-d_i(a,n)+\gamma,0)$
• 其中：$\gamma$是margin，把positive和negative拉的相对远一些，同时positive可以不那么重合

Perfect Match

• 主要就是如上两点改进

1. 使用PCA建立局部坐标系LRF

• $\Sigma \hat{S}=\frac{1}{\sum_{\|S\|}(R-d_i)}\sum_{p\in S}(p_i-p)(p_i-p)^T$
• 根据点的数量确定正方向

2. 使用triplet loss

PPFNet

• PPFNet结合了全局信息和局部信息，考虑了patch对patch的triplet loss

• PFH包含四个信息：
  • $\psi_{12}=(\|d\|_2,\angle(n_1,d),\angle(n_2,d),\angle(n_1,n_2) )$
  • $\angle(n_1,n_2)=atan2(\|v_1\times v_2\|,v_1\cdot v_2)$

• N-tuple Loss

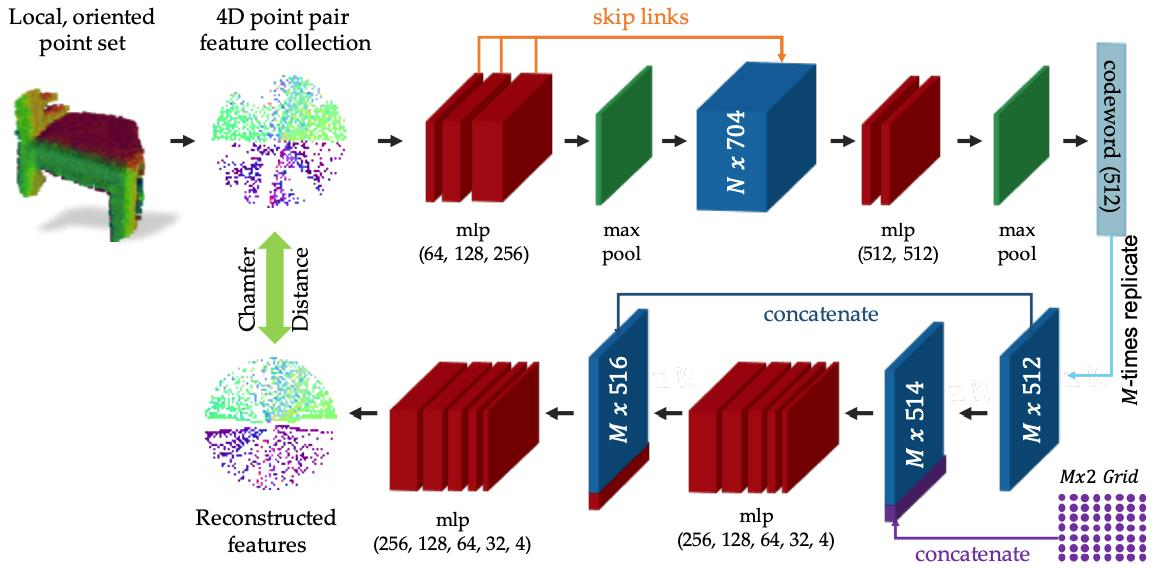
PPF-FoldNet

• PPF-FoldNet使用了autoencoder
• decoder-encoder

Registration

ICP

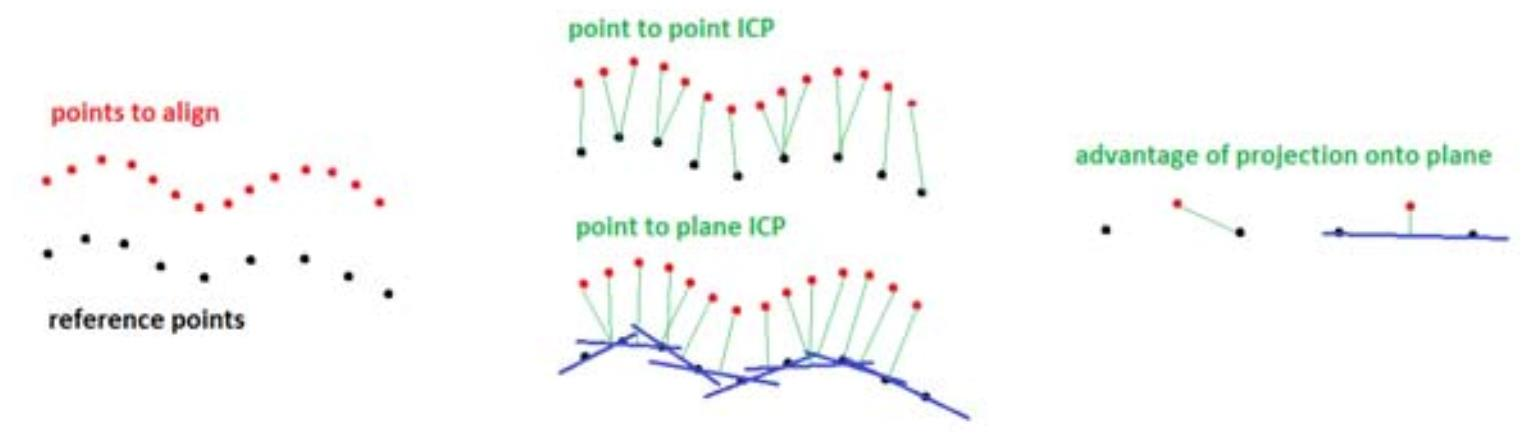
• correspondence是根据两个点的距离计算。
• 简单，但是需要初始化𝑅, 𝑡

步骤

• Given two corresponding point sets:
  • 𝑃 = {𝑝1, ⋯ , 𝑝𝑁}, 𝑝𝑖 ∈ ℝ3, we are transforming 𝑃 (source)
  • 𝑄 = {𝑞1, ⋯ , 𝑞𝑁}, 𝑞𝑖 ∈ ℝ3, assume 𝑄 is fixed (target)

1. Data association: 𝑁 correspondences

• For each point 𝑝𝑖 find the nearest neighbor in 𝑄
• Remove outlier pairs, e.g., ||𝑝𝑖 − 𝑞𝑖|| too large

2. $R,t=\argmin_{R,t}\min E(R,t)=\argmin_{R,t}\frac{1}{N}\sum_{i=1}^{N}\|q_i-Rp_i-t\|^2$

• Compute center $\mu_p=\frac{1}{N}\sum_{i=1}^{N}q_i$
• $P'=\{p_i-\mu_p\},Q'=\{q_i-\mu_q\}$
• $Q'P'^T=U\Sigma V^T$
• $R=UV^T,t=\mu_q-R\mu_p$

3. Check converge.

• Evaluate convergence criteria
  1. $E(R,t)$small enough
  2. 𝛥𝑅, 𝛥𝑡 small enough
• If not converged,
  1. 𝑃 ← 𝑅𝑃 + 𝑡
  2. repeat Step 1-3

ICP 缺点

• 找最近对应点的计算开销较大
• 只考虑了点与点距离，缺少对点云结构信息的利用

改进

1. 选取一部分点做ICP，减少计算复杂度

• Random Sample
• Voxel Grid Sample
• Normal Space Sampling (NSS)
  
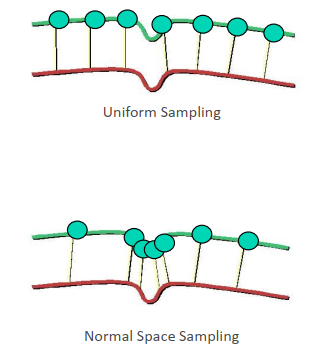
• Feature detection

2. 数据关联

• Nearest neighbor – kd-tree/octree for acceleration
• Normal shooting：投影其法向量最短的点，作为关联
  
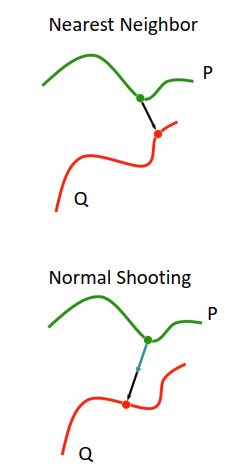
• Projection：只能在RGBD中做，通过2维坐标找关联
  
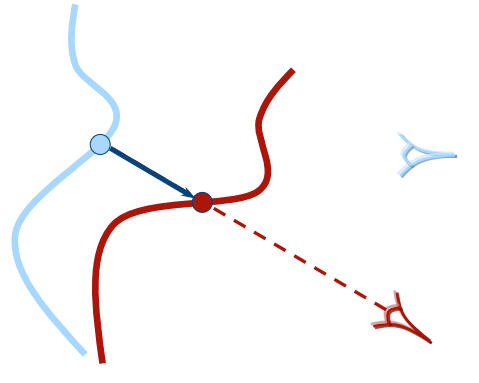
• Feature descriptor matching (compatible point)

3. 去除异常值

• Remove correspondence with high distance
• Remove worst x% of correspondences

4. Loss function

• Point-to-Point

• Point-to-Plane：点与另一个点与周围点形成的平面距离，由于是平面约束，可以在平面上移动，容易求解最优，速度快，但需要最小二乘，求解复杂
  

• 方法列举

  • Point-to-Plane ICP，原始 ICP 算法的代价函数中使用的 point-to-point 距离，point-to-plane 则是考虑源顶点到目标顶点所在面的距离，比起直接计算点到点距离，考虑了点云的局部结构，精度更高，不容易陷入局部最优；但要注意 point-to-plane 的优化是一个非线性问题，速度比较慢，一般使用其线性化近似；
  • Plane-to-Plane ICP，point-to-plane 只考虑目标点云局部结构， plane-to-plane 顾名思义就是也考虑源点云的局部结构，计算面到面的距离；
  • Generalized ICP (GICP)，综合考虑 point-to-point、point-to-plane 和 plane-to-plane 策略，精度、鲁棒性都有所提高；
  • Normal Iterative Closest Point (NICP)，考虑法向量和局部曲率，更进一步利用了点云的局部结构信息，其论文中实验结果比 GICP 的性能更好。

Point-to-Plane步骤

• Given two corresponding point sets:
  • 𝑃 = {𝑝1, ⋯ , 𝑝𝑁}, 𝑝𝑖 ∈ ℝ3, we are transforming 𝑃 (source)
  • 𝑄 = {𝑞1, ⋯ , 𝑞𝑁}, 𝑞𝑖 ∈ ℝ3, assume 𝑄 is fixed (target)

1. Data association: 𝑁 correspondences

• For each point 𝑝𝑖 find the nearest neighbor in 𝑄
• Remove outlier pairs, e.g., ||𝑝𝑖 − 𝑞𝑖|| too large

2. $R,t=\argmin_{R,t}\min E(R,t)=\argmin_{R,t}\frac{1}{N}\sum_{i=1}^{N}((Rp_i+t-q_i)^Tn_i)^2$

• $\hat{x}=\argmin_xE(x)=\|Ax-b\|^2=(A^TA)^{-1}A^Tb$
• $\hat{x}=[\alpha,\beta,\gamma,t_x,t_y,t_z]^T$
• compute R,t from $\hat{x}$

3. Check converge.

• Evaluate convergence criteria
  1. $E(R,t)$small enough
  2. 𝛥𝑅, 𝛥𝑡 small enough
• If not converged,
  1. 𝑃 ← 𝑅𝑃 + 𝑡
  2. repeat Step 1-3

NDT

• Normal Distribution Transform

1. 建立voxel，每个grid使用高斯模型来建模。如果一个格子中的点过于少就丢掉，认为格子是空的，无法建立高斯模型。

• $\vec{\mu}=\frac{1}{m}\sum_{k=1}^{m}\vec{y}_k$
• $\Sigma=\frac{1}{m-1}\sum_{k=1}^{m}(\vec{y}_k-\vec{\mu})(\vec{y}_k-\vec{\mu})^T$
• 建立出三维的高斯分布
  

2. 将source中的点，通过RT转到target frame中，然后用1）中建立的概率构建最大似然估计

• 使用mixture prob来代替高斯分布，使得对外点鲁棒
• 用高斯分布模拟最大似然中的-log函数
• 使用牛顿法来求解高斯分布的极值，从而完成优化。可以求出NDT中牛顿法的解析解，所以很快。

Feature Based Registration