void land space 主页文章标签分类相册
状态估计中的优化问题
| math

模型表示

  • 假定观测模型的数学表达：
    • zk,j=h(yi,xk,vk,j)z_{k,j}=h(y_i,x_k,v_{k,j})
    • yiy_i：每个点的坐标
    • xkx_k：相机位置
    • vk,jv_{k,j}：噪声
  • 定义状态变量x为：
    • x=[x1,⋯ ,xN,y1,⋯ ,yM]x=[x_1,\cdots,x_N,y_1,\cdots,y_M]
  • 根据x状态，z观测，u输入量，求解x的分布：
    • P(x∣z,u)=?P(x|z,u)=?

概率模型

  • 直接求P(x∣z)P(x|z)很困难，根据贝叶斯法则，可以将问题转化

    • P(x∣z)=P(z∣x)P(x)P(z)∝P(z∣x)P(x)P(x|z)=\frac{P(z|x)P(x)}{P(z)}\propto P(z|x)P(x)
    • P(z∣x)P(z|x)：似然概率
    • P(x)P(x)：先验概率

  • 最大后验估计(Maximize a Posterior,MAP)

    • xMAP∗=arg⁡max⁡P(x∣z)=arg⁡max⁡P(z∣x)P(x)x^*_{MAP}=\arg\max P(x|z)=\arg\max P(z|x)P(x)
    • 在没有P(x)P(x)先验概率情况下，求得最大的P(z∣x)P(z|x)似然概率也可以得到最大的后验概率

  • 最大似然估计(Maximize Likelihood Estimation,MLE)

    • xMLE∗=arg⁡max⁡P(z∣x)x^*_{MLE}=\arg\max P(z|x)

最优估计问题

  • 根据观测模型
    • zk,j=h(yi,xk)+vk,jz_{k,j}=h(y_i,x_k)+v_{k,j}
  • 假设vk,jv_{k,j}符合高斯分布：
    • vk,j∼N(0,Qk,j)v_{k,j}\sim N(0,Q_{k,j})
  • 所以，在已知xk,yjx_k,y_j的条件下，状态zj,kz_{j,k}满足正态分布
    • P(zj,k∣xk,yj)=N(h(yj,xk),Qk,j)P(z_{j,k}|x_k,y_j)=N(h(y_j,x_k),Q_{k,j})
    • 期望由xk,yjx_k,y_j决定，方差由高斯噪声Qk,jQ_{k,j}决定
  • 求x,y的最大似然估计

最小二乘问题

  • 高斯分布的形式
    • P(x)=1(2π)Ndet⁡(∑)e−12(x−μ)T∑−1(x−μ)P(x)=\frac{1}{\sqrt{(2\pi)^N\det(\sum)}}e^{-\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)}
    • ∑\sum：协方差
  • 最大似然法，求最大P(x)的分布，转换为负对数形式求取−ln(P(x))-ln(P(x))的最小值
    • −ln(P(x))=12((2π)Ndet⁡(∑))+12(x−μ)T∑−1(x−μ)-ln(P(x))=\frac{1}{2}((2\pi)^N\det(\sum))+\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)
    • 12((2π)Ndet⁡(∑))\frac{1}{2}((2\pi)^N\det(\sum))与x没有关系，只跟12(x−μ)T∑−1(x−μ)\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)有关，这个二次型是马氏距离
  • 将最大似然估计等价为最小二乘的问题，定义损失函数
    • 原问题：{xk=f(xk−1,uk,wk)zk,j=h(xk,yj,vk,j)\begin{cases}x_k=f(x_{k-1},u_k,w_k)\\z_{k,j}=h(x_k,y_j,v_{k,j})\end{cases}
    • 误差：{ev,k=xk−f(xk−1,uk)ey,k,j=zk,j−h(xk,yj)\begin{cases}e_{v,k}=x_k-f(x_{k-1},u_k)\\e_{y,k,j}=z_{k,j}-h(x_k,y_j)\end{cases}
    • min⁡J(x)=∑kev,kTRk−1ev,k+∑k∑jey,k,jTQk,j−1ey,k,j\min J(x)=\sum_k{e_{v,k}^{T}R_{k}^{-1}e_{v,k}}+\sum_k\sum_j{e_{y,k,j}^{T}Q_{k,j}^{-1}e_{y,k,j}}
    • R和Q是I时为二范数，不为I时可以调整优化的方向

非线性最小二乘问题求解

  • 考虑一个简单问题：

    • arg⁡min⁡x12∥f(x)∥22\arg\min_x\frac{1}{2}\left\|f(x)\right\|_2^2，
    • 其中：x∈R3x\in\mathbb{R}^3，f为任意函数

  • 当f很简单时，可直接求导为0，得到鞍点、极小值解，对比就可以得到最优解

  • 当f很复杂时，可以用迭代的方式求解

  • 迭代时增量的确定：

    • 泰勒展开：∥f(x+△x)∥22≈∥f(x)∥22+J(x)△x+12△xTH△x+⋯\left\|f(x+\triangle x)\right\|_2^2\approx\left\|f(x)\right\|_2^2+J(x)\triangle x+\frac{1}{2}\triangle x^TH\triangle x+\cdots
    • 其中J(x)为雅克比矩阵，H(x)为海森矩阵

  • 最速下降法：只保留一阶梯度

    • △x∗=arg⁡min⁡∥f(x)∥22+J(x)△x\triangle x^*=\arg\min\left\|f(x)\right\|_2^2+J(x)\triangle x
    • 增量方向为：△x∗=−JT(x)\triangle x^*=-J^T(x)

  • 牛顿法：保留二阶梯度

    • △x∗=arg⁡min⁡∥f(x)∥22+J(x)△x+12△xTH△x\triangle x^*=\arg\min\left\|f(x)\right\|_2^2+J(x)\triangle x+\frac{1}{2}\triangle x^TH\triangle x
    • 令上式关于△x\triangle x导数为0：H△x=−JTH\triangle x=-J^T

  • 使用牛顿法迭代次数少，更好的利用全局信息。但海森矩阵的计算比较复杂，有两种方法可以简化：

    • Gauss-Newton
    • Levenberg-Marquadt

Gauss-Newton

  • 一阶近似f(x)：
    • f(x+△x)≈f(x)+J(x)△xf(x+\triangle x)\approx f(x)+J(x)\triangle x
  • 平方误差变为：
    • 12∥f(x)+J(x)△x∥22=12(f(x)+J(x)△x)T(f(x)+J(x)△x)=12(∥f(x)∥22+2f(x)TJ(x)△x+△xTJ(x)TJ(x)△x)\frac{1}{2}\left\|f(x)+J(x)\triangle x\right\|_2^2=\frac{1}{2}(f(x)+J(x)\triangle x)^T(f(x)+J(x)\triangle x)=\frac{1}{2}(\left\|f(x)\right\|_2^2+2f(x)^TJ(x)\triangle x+\triangle x^TJ(x)^TJ(x)\triangle x)
  • 令关于△x\triangle x导数为0：
    • 2J(x)Tf(x)+2J(x)TJ(x)△x=02J(x)^Tf(x)+2J(x)^TJ(x)\triangle x=0
    • J(x)TJ(x)△x=−J(x)Tf(x)J(x)^TJ(x)\triangle x=-J(x)^Tf(x)
    • 记为：H△x=gH\triangle x=g，这里的H使用两个雅克比近似的，不需要计算海森矩阵
  • GN计算出的H无法保证H可逆，无法得到确定的增量：△xk=H−1g\triangle x_k=H^{-1}g

Levenberg-Marquadt

  • GN属于线搜索方法，先找到方向，再确定长度
  • LM是对GN的优化，属于信赖区域(Trust Region)方法，认为近似只在区域内可靠，增强H的正定性
    • 考虑是否是一个二次函数的近似程度的描述，是否能够用雅克比近似：
      • p=f(x+△x)−f(x)J(x)△xp=\frac{f(x+\triangle x)-f(x)}{J(x)\triangle x}
      • 若太小，则减小近似范围
      • 若太大，则增加近似范围
  • Trust Region内的优化，利用Lagrange乘子转化为无约束
    • min⁡△xk12∥f(xk)+J(xk)△xk∥2+λ2∥D△x∥2\min_{\triangle x_k}\frac{1}{2}\left\|f(x_k)+J(x_k)\triangle x_k\right\|^2+\frac{\lambda}{2}\left\|D\triangle x\right\|^2
    • 按照G-N展开，增量方程为：
    • (H+λDTD)△x=g(H+\lambda D^TD)\triangle x=g
  • 在算法中取D=I，即一个正圆形状，则：
    • (H+λI)△x=g(H+\lambda I)\triangle x=g
    • (H+λI)(H+\lambda I)，保证了正定性
    • 是一阶和二阶的混合，可以调整λ\lambda的大小，来控制圆的范围，控制更像高斯牛顿还是更像梯度

极大似然估计(MLE)

  • 假设我们有一个概率模型，例如是高斯分布模型N(μ,σ)N(\mu,\sigma)，利用这个模型，我们生成很多数据{x1,x2…xN}\{x_{1},x_{2} \dots x_{N}\}，这是利用模型生成数据的过程[1]。
  • 但如果反过来，我们有一批数据{x1,x2…xN}\{x_{1},x_{2} \dots x_{N}\}，想根据这批数据估计模型的参数，例如高斯分布模型的μ,σ\mu,\sigma，这就是估计过程。常见的估计方法有极大似然估计、最大后验概率估计、贝叶斯估计等。含有隐变量的极大似然估计就是大名鼎鼎的EM算法。

似然函数

  • 有一组数据，f(x,Θ)f(x,\Theta)，其中：
    • x是i.i.d(独立同分布，Independent and identical distribution)的一组抽样
    • Θ\Theta是分布模型，模型类型和参数都未知，设有k个参数：{θ1,⋯ ,θn}\{\theta_1,\cdots,\theta_n\}
  • 似然函数就是在利用现有样本情况下，假定模型和参数可以生成这些样本的联合概率密度
    • L(x1,⋯ ,xn;θ1,⋯ ,θk)=∏i=1nf(xi;θ1,⋯ ,θk)L(x_1,\cdots,x_n;\theta_1,\cdots,\theta_k)=\prod_{i=1}^{n}f(x_i;\theta_1,\cdots,\theta_k)
  • 所以似然函数其实就是样本点的联合概率密度函数，只不过自变量变成了概率分布模型的参数Θ。似然函数一般形式如下
    • 简化为：L(x,Θ)=L(θ∣x)=p(x∣Θ=θ)=p(x;Θ=θ)L(x,\Theta)=L(\theta|x)=p(x|\Theta=\theta)=p(x;\Theta=\theta)
    • p(x∣θ)p(x|\theta)和p(x;θ)p(x;\theta)表示一个意思：在给定模型参数是θ的条件下，x的概率，与x和θ的联合概率分布结果是一样的
  • 一个似然函数乘以一个正的常数之后仍然是似然函数。所以L(θ∣x)=αp(x∣Θ=θ),α>0L(\theta|x)=\alpha p(x|\Theta = \theta),\alpha > 0。
  • 似然和概率是两码事，概率描述了已知概率模型参数时的随机变量的输出结果；似然则用来描述已知随机变量输出结果时，未知概率模型参数的可能取值，也就是说，概率使用背景是模型参数已知，似然是模型参数未知。

极大似然估计

  • Maximum Likelihood Estimation，最大似然估计，一般用对数似然函数，对其求导取驻点得到要求的θ：
    • log⁡L(θ1,⋯ ,θk)=∑i=1nlog⁡f(xi;θ1,⋯ ,θk)\log{L(\theta_1,\cdots,\theta_k)}=\sum_{i=1}^{n}\log{f(x_i;\theta_1,\cdots,\theta_k)}
    • 求导为0：∂L(θ)θi=0,  i=1,2,⋯ ,k\frac{\partial L(\theta)}{\theta_i}=0,\;i=1,2,\cdots,k
  • 在很多场合下，最大似然估计与极大似然估计是一种东西的两种叫法，理论上我们应该是要求最大似然估计，但是由于我们是求对数似然函数的驻点得到，严格来说求得是极值点，所以也叫极大似然估计，在指数族框架下的概率密度函数，极值就是最值。我个人倾向于叫极大似然估计。

最大后验概率估计

  • Maximum A Posteriori(MAP)，MAP是贝叶斯学派常用的估计方法

  • 上面说过，极大似然估计就是求解下面的式子(直接表示成了对数似然函数)：

    • arg⁡max⁡θlog⁡p(x∣θ)\arg\max_\theta\log{p(x|\theta)}

  • 这里模型参数θ是确定但是未知的，我们假设了参数θ的取值，例如伯努利分布中的p参数，才能对上式进行进一步的数学求解。

  • 如果我们知道了模型参数θ的一些先验分布，我们就要用最大后验概率估计来求解参数θ，最大后验概率估计主要求解下面的式子：

    • arg⁡max⁡θp(θ∣x)\arg\max_\theta p(\theta|x)

  • p(θ∣x)p(\theta|x)就是后验概率，这也是最大后验概率名字的由来。用贝叶斯公式展开就是

    • arg⁡max⁡θp(x∣θ)p(θ)p(x)\arg\max_\theta\frac{p(x|\theta)p(\theta)}{p(x)}

  • 考虑到分母和θ无关，因此在求解上式时直接舍去，同时转化为对数形式有

    • arg⁡max⁡θlog⁡p(x∣θ)p(θ)=arg⁡max⁡θ(log⁡p(x∣θ)+log⁡p(θ))\arg\max_\theta\log p(x|\theta)p(\theta)=\arg\max_\theta(\log p(x|\theta)+\log p(\theta))

  • 可以看到最大后验概率估计的前半部分就是似然函数，后面部分是参数的先验分布，我们可以认为模型参数θ满足高斯分布或者beta分布。以参数θ满足均值是0.5，方差是0.1的高斯分布为例可得

    • arg⁡max⁡θ(log⁡p(x∣θ)+log⁡p(θ))\arg\max_\theta(\log p(x|\theta)+\log p(\theta))
    • arg⁡max⁡θ(log⁡p(x∣θ)+log⁡12π×0.1exp(−(θ−0.5)22×0.1)))\arg\max_\theta(\log p(x|\theta)+\log\frac{1}{\sqrt{2\pi\times 0.1}}exp(-\frac{(\theta-0.5)^2}{2\times 0.1})))

  • 所以，最大后验概率估计可以看作是规则化（regularization）的最大似然估计，这点在求解对数形式函数时更加的明显(此时同机器学习模型一样是加性的规则化，不是乘性的)。

  • 求解最大后验概率估计就是对上面的式子求导取极值点，方法和极大似然估计类似，求出的结果是一个确定的点。

贝叶斯估计(BE)

  • 贝叶斯估计看名字，也知道主要在使用贝叶斯公式，和最大后验概率估计的前半截一样，后面的步骤不同。前半截同MAP一样，求参数θ的后验概率
    • p(θ∣x)=p(x∣θ)p(θ)p(x)p(\theta|x)=\frac{p(x|\theta)p(\theta)}{p(x)}
  • 由于分母和参数θ没有任何关系，只考虑分子部分
    • θ^∗=arg max⁡θαp(x∣θ)p(θ)\hat{\theta}^*=\argmax_\theta \alpha p(x|\theta)p(\theta)
  • 其中α是与θ无关的部分
  • 最大后验概率估计认为θ是一个确定但未知的参数，所以MAP认为上式是关于θ的一般函数，就把估计问题转变成了优化问题，找到参数θ使得上式最大，可以使用导数等优化方法，求得的最值点就是参数θ的估计值。
  • 但是在贝叶斯估计中，认为参数θ是一个未知的变量，所以贝叶斯估计认为上式是p(θ∣x)p(\theta|x)的后验概率密度函数。我们要求的参数θ的估计值θ^\hat{\theta} ，要满足最小化下面的期望损失函数
    • arg⁡min⁡θ∫f(θ^,θ)p(θ∣x)dθ\arg\min_\theta\int f(\hat{\theta},\theta)p(\theta|x)d\theta
    • 其中：θ^\hat{\theta}是估计值
    • f(θ^,θ)f(\hat{\theta},\theta)是损失函数，一般可以选择二阶损失：f(θ^,θ)=(θ^−θ)2f(\hat{\theta},\theta)=(\hat{\theta}-\theta)^2
  • 使用二阶损失带入：
    • =∫(θ^−θ)2p(θ∣x)dθ=\int(\hat{\theta}-\theta)^2p(\theta|x)d\theta
    • =θ^2∫p(θ∣x)dθ−2θ^∫θp(θ∣x)dθ+∫θ2p(θ∣x)dθ=\hat{\theta}^2\int p(\theta|x)d\theta-2\hat{\theta}\int\theta p(\theta|x)d\theta+\int\theta^2p(\theta|x)d\theta
  • 对θ^\hat{\theta}求导：
    • θ^∗=∫θp(θ∣x)dθ∫p(θ∣x)dθ\hat{\theta}^*=\frac{\int\theta p(\theta|x)d\theta}{\int p(\theta|x)d\theta}
  • 由于∫p(θ∣x)dθ=1\int p(\theta|x)d\theta=1，最终可得：
    • θ^∗=∫θp(θ∣x)dθ\hat{\theta}^*=\int\theta p(\theta|x)d\theta
  • 也就是参数θ的后验概率期望，即是贝叶斯估计的最终估计结果。
  • 综上，贝叶斯估计根据参数的先验分布P(θ)P(\theta)和一系列观察X，求出参数θ的后验分布P(θ∣X)P(\theta|X)，然后求出θ的期望值，作为其最终值。
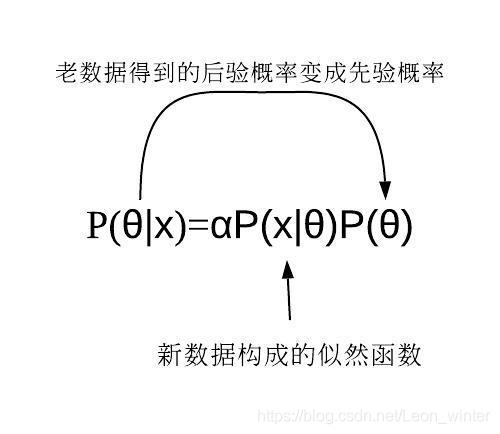
  • 贝叶斯估计可以迭代使用：在观察一些数据后，利用BE求得到后验概率，可以当作新的先验概率，再根据新的数据得到新的后验概率。因此贝叶斯定理可以应用在许多不同的证据上，不论这些证据是一起出现或是不同时出现都可以，这个程序称为贝叶斯更新（Bayesian updating）。

MLE\MAP\BE比较

  • 在MLE中，θ应该是已经确定但是未知的，所以MLE求得的结果是参数θ的一个点。
  • 在MAP中，θ同样是已经确定但是未知的，但是与MLE不同的是，MAP考虑了先验知识，也就是参数θ根据我们的经验，满足一个概率分布，MLE求得的结果同样是参数θ的一个点。
  • 在BE中，θ压根就是未知的变量，我们利用贝叶斯定理得到了参数θ的后验概率分布，而不是MLE或MAP那样得到一个点，只不过我们最终取后验概率期望为我们最终的估计值。

举例

  • 100次抛硬币，60次正面40次反面，问下一次正面的概率

MLE

  • 已知抛硬币满足二项分布：
    • Cnkpk(1−p)n−kC_n^kp^k(1-p)^{n-k}
  • 定义方程，并将已知量带入：
    • L(p)=C10060p60(1−p)40,  p∈(0,1)L(p)=C_{100}^{60}p^{60}(1-p)^{40},\;p\in(0,1)
  • 求最大对数似然的极值：
    • ln⁡L(p)=C10060(60ln⁡p+40ln⁡1−p\ln{L(p)}=C_{100}^{60}(60\ln{p}+40\ln{1-p}
    • dln⁡L(p)dp=C10060(60p+40p−1)=0\frac{d\ln{L(p)}}{dp}=C_{100}^{60}(\frac{60}{p}+\frac{40}{p-1})=0
    • 60p+40p−1=100p−60p2−p=0\frac{60}{p}+\frac{40}{p-1}=\frac{100p-60}{p^2-p}=0
    • p=0.6p=0.6

MAP

  • 对于抛硬币，我们有先验分布：
    • P(A=1)=0.5P(A=1)=0.5，不包括竖起来的情况
  • 假设硬币正反的概率服从θ∼N(0.5,12)\theta\sim N(0.5,1^2)的分布，利用贝叶斯公式，得到后验概率：
    • p(θ∣x)=p(x∣θ)p(θ)=θ60(1−θ)4012πe−12(θ−0.51)2p(\theta|x)=p(x|\theta)p(\theta)=\theta^{60}(1-\theta)^{40}\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{\theta-0.5}{1})^2}
  • 求极值：
    • ln⁡L(θ)=ln⁡p(x∣θ)+ln⁡p(θ)=60log⁡θ+40ln⁡1−θ+ln⁡12π−12(θ−0.5)2\ln{L(\theta)}=\ln p(x|\theta)+\ln p(\theta)=60\log{\theta}+40\ln{1-\theta}+\ln{\frac{1}{\sqrt{2\pi}}}-\frac{1}{2}(\theta-0.5)^2
    • dln⁡L(θ)dθ=0\frac{d\ln{L(\theta)}}{d\theta}=0
    • 60θ+40θ−1−(θ−0.5)=0\frac{60}{\theta}+\frac{40}{\theta-1}-(\theta-0.5)=0
    • 100θ−60−(θ−0.5)(θ2−θ)=0100\theta-60-(\theta-0.5)(\theta^2-\theta)=0
    • θ3+1.5θ2−99.5θ+60=0\theta^3+1.5\theta^2-99.5\theta+60=0
    • 只有一个是符合0~1的：θ=0.61\theta=0.61
  • 求出的概率和分布、统计值都相关，分布越分散，概率越远离0.5，同样统计越不平均，概率也就偏离的越大

BE[2]

  • 硬币为正面的概率

    • E(θ∣x)=∫01θp(θ∣x)dθE(\theta|x)=\int_0^1\theta p(\theta|x)d\theta

  • 后验概率

    • E(θ∣x)=m+am+a+l+bE(\theta|x)=\frac{m+a}{m+a+l+b}
    • 其中：
    • a: 先验分布的正面向上次数
    • b: 先验分布的反面向上次数
    • m: 已观测数据的正面向上次数，60
    • l: 已观测数据的反面向上次数，40

  • 假设先验分布为高斯分布，定义a,b都为10，若你坚信硬币向上的概率肯定是0.5，那么可以调大a和b的值。

  • 带入式子可得：

    • 60+1060+40+10+10=0.58\frac{60+10}{60+40+10+10}=0.58

  • 这个就是修正后的后验概率，介于先验和观测之间的值

  • 由例子可知，即使先验分布符合高斯分布且正面向上的概率在0.5达到最大，但是如果观测数据倾向于正面向上，则最终的判断结果会倾向于正面向上，贝叶斯思想有点像是风往哪边吹树就往哪边倒的意思。当观测结果的正面向上次数远远大于正面向下次数，也远远大于先验分布的正面向下次数，则判断下次为正面向上的概率无限接近1。

  1. 链接 ↩︎

  2. 链接 ↩︎

optimization