void land space 主页文章标签分类相册
三维重建
| programme

简介

  • 三维重建包含静态场景、动态场景。目前是一个非常热的研究领域，未来会在很多领域发挥巨大作用
    • 室内场景：稠密三维重建目的是使用消费级相机（本文特指深度相机）对室内场景进行扫描，自动生成一个精确完整的三维模型，应用在室内的增强现实游戏、机器人室内导航、AR家具展示等。
    • 室外场景主要应用在自动驾驶、建筑建模等场景

特征点提取和检测

定义

  • 在其他含有相同场景或目标的相似图像中以一种相同的或至少非常相似的不变形式表示图像或目标。具有尺度不变性。

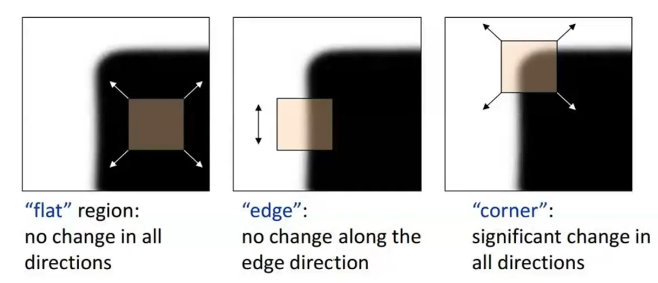
特征点类型

  • 角点作为特征点最具代表性，在两个方向上都具有强烈变化。边缘和区块相对难以区分。

特征

  • 可重复性(Repeatability)：相同区域可以在不同的图像中被找到
  • 可区别性(Distinctiveness)：不同区域有不同的表达
  • 高效性(Efficiency)：同一图像中，特征点的数量应远小于像素的数量
  • 局部性(Locality)：特征仅与一小片图像区域有关

组成

  • 关键点(Key Point)；位置、大小、方向、评分等
    • FAST/Moravec/Harris
  • 描述子(Descriptor)：特征点周围的图像信息，对旋转、平移、噪声等干扰具有抵抗能力
    • SIFT/SURF/ORB/BRIEF/BRISK

关键点检测

Harris角点检测

  • 在(x,y)这个点统计x,y的变化率，得到变换方向[u,v]和Harris矩阵，再根据SVD分解，可以得到两个特征值，得到在两个方向的变化情况。若两个特征点都变化较大，则为角点

  • E(u,v)=∑x,y[I(x+u,y+v)−I(x,y)]2≈∑x,yw(x,y)[I(x,y)+∂I∂x(x,y)u+∂I∂y(x,y)v−I(x,y)]2=[uv]TH[uv]E(u,v)=\sum_{x,y}[I(x+u,y+v)-I(x,y)]^2\approx\sum_{x,y}w(x,y)[I(x,y)+\frac{\partial I}{\partial x}(x,y)u+\frac{\partial I}{\partial y}(x,y)v-I(x,y)]^2=\begin{bmatrix}u\\v\end{bmatrix}^TH\begin{bmatrix}u\\v\end{bmatrix}

    • 图像梯度：△I(x,y)=(∂I∂x(x,y),∂I∂y(x,y))\triangle I(x,y)=(\frac{\partial I}{\partial x}(x,y),\frac{\partial I}{\partial y}(x,y))
    • Harris矩阵：H=[∑x,yw(x,y)(∂I∂x(x,y))2∑x,yw(x,y)(∂I∂x(x,y)∂I∂y(x,y))sumx,yw(x,y)(∂I∂x(x,y)∂I∂y(x,y))∑x,yw(x,y)(∂I∂y(x,y))2]H=\begin{bmatrix}\sum_{x,y}w(x,y)(\frac{\partial I}{\partial x}(x,y))^2&\sum_{x,y}w(x,y)(\frac{\partial I}{\partial x}(x,y)\frac{\partial I}{\partial y}(x,y))\\\\sum_{x,y}w(x,y)(\frac{\partial I}{\partial x}(x,y)\frac{\partial I}{\partial y}(x,y))&\sum_{x,y}w(x,y)(\frac{\partial I}{\partial y}(x,y))^2\end{bmatrix}

  • SVD(H)=UΣVSVD(H)=U\Sigma V，λ1,λ2\lambda_1,\lambda_2

    • 根据λ1,λ2\lambda_1,\lambda_2判断是否为角点

  • 为了简化SVD求解，使用角点准则：C=det(H)−ktrace(H)2=λ1λ2−k(λ1+λ2)2C=det(H)-ktrace(H)^2=\lambda_1\lambda_2-k(\lambda_1+\lambda_2)^2,k=0.04

    • k越小，检测子越敏感
    • 只有当λ1λ2\lambda_1\lambda_2同时取得最大值时，c才能取得最大

  • 非极大值抑制(NMS)，避免重复检测

缺点

  • 不具有尺度不变性

LoG特征点检测

  • 尺度归一化的LoG算子，模拟人的视觉由近到远的特点，得到多个尺度空间的特征点
  • 尺度空间，用不同大小的滤波核k对图像滤波，得到多个图：L(x,y,σD)=I(x,y)∗G(x,y,σD),  σD∈[σ0,kσ0,k2σ0,...]L(x,y,\sigma_D)=I(x,y)*G(x,y,\sigma_D),\;\sigma_D\in[\sigma_0,k\sigma_0,k^2\sigma_0,...]
  • LoG算子：▽L(x,y,σD)=(∂2L(x,y,σD)∂x2+∂2L(x,y,σD)∂y2)=(∂2G(x,y,σD)∂x2+∂2G(x,y,σD)∂y2)∗I(x,y)\triangledown L(x,y,\sigma_D)=(\frac{\partial^2L(x,y,\sigma_D)}{\partial x^2}+\frac{\partial^2L(x,y,\sigma_D)}{\partial y^2})=(\frac{\partial^2G(x,y,\sigma_D)}{\partial x^2}+\frac{\partial^2G(x,y,\sigma_D)}{\partial y^2})*I(x,y)
    • L(x,y,σD)L(x,y,\sigma_D)是拉普拉斯算子
    • G(x,y,σD)G(x,y,\sigma_D)是高斯函数
    • 卷积之后乘以拉普拉斯算子等价于高斯*原图，高斯滤波的基本性质
  • 尺度归一化的LoG：▽norm2L(x,y,σD)=σD2(∂2G(x,y,σD)∂x2+∂2G(x,y,σD)∂y2)∗I(x,y)\triangledown^2_{norm}L(x,y,\sigma_D)=\sigma_D^2(\frac{\partial^2G(x,y,\sigma_D)}{\partial x^2}+\frac{\partial^2G(x,y,\sigma_D)}{\partial y^2})*I(x,y)
  • 构建尺度空间，同时在位置空间和尺度空间寻找归一化LoG极值作为特征点

缺点

  • 计算量非常大，实际很少使用

SIFT

  • 尺度不变特征变换（SIFT）

  • 针对LOG的缺点，使用DoG对归一化LoG进行近似

  • 高斯空间：L(x,y,σ)=G(x,y,σ)∗I(x,y)L(x,y,\sigma)=G(x,y,\sigma)*I(x,y)

  • 高斯差分：D(x,y,σ)=(G(x,y,kσ)−(x,y,σ))∗I(x,y)=L(x,y,kσ)−L(x,y,σ)D(x,y,\sigma)=(G(x,y,k\sigma)-(x,y,\sigma))*I(x,y)=L(x,y,k\sigma)-L(x,y,\sigma)

步骤

  1. 尺度空间的极值检测：
    • 尺度空间指一个变化尺度(σ)的二维高斯函数G(x,y,σ)与原图像I(x,y)卷积（即高斯模糊）后形成的空间,尺度不变特征应该既是空间域上又是尺度域上的局部极值。极值检测的大致原理是根据不同尺度下的高斯模糊化图像差异（Difference of Gaussians,DoG）寻找局部极值，这些找到的极值所对应的点被称为关键点或特征点。
  2. 关键点定位：
    • 在不同尺寸空间下可能找出过多的关键点，有些关键点可能相对不易辨识或易受噪声干扰。该步借由关键点附近像素的信息、关键点的尺寸、关键点的主曲率来定位各个关键点，借此消除位于边上或是易受噪声干扰的关键点。
  3. 方向定位：
    • 为了使描述符具有旋转不变性，需要利用图像的局部特征为给每一个关键点分配一个基准方向。通过计算关键点局部邻域的方向直方图，寻找直方图中最大值的方向作为关键点的主方向。
  4. 关键点描述子：
    • 找到关键点的位置、尺寸并赋予关键点方向后，将可确保其移动、缩放、旋转的不变性。此外还需要为关键点建立一个描述子向量，使其在不同光线与视角下皆能保持其不变性。SIFT描述子是关键点邻域高斯图像梯度统计结果的一种表示，见下图。通过对关键点周围图像区域分块，计算块内梯度直方图，生成具有独特性的向量，这个向量是该区域图像信息的一种抽象，具有唯一性。Lowe在原论文中建议描述子使用在关键点尺度空间内44的窗口中计算的8个方向的梯度信息，共44*8=128维向量表征。(opencv中实现的也是128维)

SURF

  • (Speeded-Up Robust Features) 加速稳健特征
    SURF(Speeded Up Robust Features, 加速稳健特征) 是一种稳健的图像识别和描述算法。它是SIFT的高效变种，也是提取尺度不变特征，算法步骤与SIFT算法大致相同，但采用的方法不一样，要比SIFT算法更高效（正如其名）。SURF使用海森(Hesseian)矩阵的行列式值作特征点检测并用积分图加速运算；SURF 的描述子基于 2D 离散小波变换响应并且有效地利用了积分图。

步骤

  1. 特征点检测：
    • SURF使用Hessian矩阵来检测特征点，该矩阵是x,y方向的二阶导数矩阵，可测量一个函数的局部曲率，其行列式值代表像素点周围的变化量，特征点需取行列式值的极值点。用方型滤波器取代SIFT中的高斯滤波器，利用积分图（计算位于滤波器方型的四个角落值）大幅提高运算速度。
  2. 特征点定位：
  • 与SIFT类似，通过特征点邻近信息插补来定位特征点。
  1. 方向定位：
    • 通过计算特征点周围像素点x,y方向的哈尔小波变换，并将x,y方向的变换值在xy平面某一角度区间内相加组成一个向量，在所有的向量当中最长的(即x、y分量最大的)即为此特征点的方向。
  2. 特征描述子：
    • 选定了特征点的方向后，其周围相素点需要以此方向为基准来建立描述子。此时以55个像素点为一个子区域，取特征点周围2020个像素点的范围共16个子区域，计算子区域内的x、y方向(此时以平行特征点方向为x、垂直特征点方向为y)的哈尔小波转换总和Σdx、ΣdyΣdx、Σdy与其向量长度总和Σ|dx|、Σ|dy|Σ|dx|、Σ|dy|共四个量值，共可产生一个64维的描述子。

FAST

  • 是一种角点检测，主要检测局部像素灰度变化明显的地方，以速度快著称
  • 如果一个像素与它邻域的像素差别较大，则其更有可能是角点。

角点

  • 计算过程：

    • 在图像中选取像素p，假设亮度为Ip
    • 设置阈值T（比如Ip的20%）
    • 以像素为中心，选取半径为3的圆上的16个像素点
    • 选取的圆上，若有连续的N个点亮度大于Ip+T或小于Ip-T

  • N的取值的不同，可以分为：FAST-9、FAST-11、FAST-12。常用的FAST-12

Oriented FAST

  • 由于相机的旋转，相同的角点会有旋转变化，按照相同矩形框范围计算描述子会导致结果的不同
  • Oriented FAST在FAST基础上，计算旋转，得到的选择框可以与之前的检测更为相似，具体过程：
    • 在一个细小的图像块B中，定义图像块的矩为：
      • mpq=∑x,y∈BxpyqI(x,y),  p,q=0,1m_{pq}=\sum_{x,y\in B}x^py^qI(x,y),\;p,q={0,1}
    • 通过矩可以找到图像块的质心：
      • C=(m10m00,m01m00)C=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}})
    • 链接图像块的几何中心O与质心C，得到一个方向向量OC→\overrightarrow{OC}，特征点的方向可以定义为
      • θ=arctan(m01m10)\theta=arctan(\frac{m_{01}}{m_{10}})

描述子

  • 基于直方图
  • 基于不变性
  • 基于二进制

SIFT描述子

  • 生成描述子，统计不同方向的梯度值得到直方图，找到主方向
    • 将区域分成4x4的block，每个block统计梯度方向的直方图
  • 图像根据主方向进行对齐，然后插值得到新的图像
  • 像素归一化，用户去除光照变化

GLOH描述子

  • 使用极坐标系，根据距离统计直方图

BRIEF

  • 是一种二进制描述，对特征点区域的block中，选取很多对点，每对点与特征点呈中心对称，计算两者的像素差，这种方法对光照的变化非常鲁棒

  • 算法具体过程：

    • 为减少噪声干扰，先对图像进行高斯滤波(方差为2，高斯窗口为9×9)
    • 以特征点为中心，取S×S的邻域窗口，在窗口内随机选取一对(两个)点，比较二者像素的大小，进行二进制赋值：
      • τ(p;x,y)={1if  p(x)<p(y)0otherwise\tau(p;x,y)=\begin{cases} 1 & if\;p(x)<p(y)\\0&otherwise\end{cases}
    • 其中，p(x)、p(y)分别是随机点x=(u1,v1)，y=(u2,v2)的像素值
    • 在窗口中随机选取N对随机点，重复步骤2的二进制赋值，形成一个二进制编码，这个编码就是对特征点的描述，即特征描述子。

  • BRIEF-128/256/512：在特征点附近的128次像素比较

  • 度量需要用汉明距离

    • 两个二进制的值进行比较，得到两者不同的位数

随机选点

  • 随机选点的方法

    1. xix_i，yiy_i都呈均匀分布[−S2,S2][-\frac{S}{2},\frac{S}{2}]
    2. xix_i，yiy_i都呈高斯分布[0,125S2][0,\frac{1}{25}S^2]，准则采样服从各向同性的同一高斯分布
    3. xix_i服从高斯分布[0,125S2][0,\frac{1}{25}S^2]，yiy_i服从高斯分布[xi,1100S2][x_i,\frac{1}{100}S^2]，采样分为2步进行，首先在原点处为xix_i进行高斯采样，然后在中心为xix_i处为yiy_i进行高斯采样
    4. xix_i，yiy_i在空间量化极坐标下的离散位置处进行随机采样
    5. xi=(0,0)Tx_i=(0,0)^T，yiy_i在空间量化极坐标下的离散位置处进行随机采样

  • 作者实验证明第2种方法效果更好

经典特征点

  • Harris
  • SIFT
  • SURF

特征点匹配

  • 特征匹配：通过描述子的差异判断哪些特征为同一个点，ORB可以用汉明距离
  • 暴力匹配：比较两图每个特征间的距离

特征匹配

  • 特征提取就是关键点和描述子的组合
  • 度量描述子的距离：欧氏距离，马氏距离，归一化互相关，汉明距离
  • 匹配策略：最近邻搜索，最近邻距离比，快速最近邻搜索

ORB特征

  • 关键点：Oriented FAST，计算了特征点的主要方向，增加了旋转不变性
  • 描述子：BRIEF，对前一步的特征点周围图像区域进行描述

相机模型

针孔相机模型

径向畸变

2D-2D对极几何

对极约束

本质/单应矩阵

三角量测

3D-2D PnP问题

  • 已知三维点和对应的二维点，求相机的内外参数

直接线性变换法

捆绑调整BA

  • 同时对三维点位置和相机参数进行非线性优化，求最小化重投影误差
  • 无约束最小二乘问题：梯度下降法、牛顿法、Levenberg-Marquardt法

静态场景[1][2]

KinectFusion

  • 帝国理工的Newcombe等人在2011年提出的KinectFusion，可在不需要RGB图而只用深度图的情况下就能实时地建立三维模型。KinectFusion算法首次实现了基于廉价消费类相机的实时刚体重建，在当时是非常有影响力的工作，它极大的推动了实时稠密三维重建的商业化进程。

  • 论文

  • 代码

  • PCL实现的代码

Kintinuous

ElasticFusion

ElasticReconstruction

DynamicFusion

InfiniTAM

BundleFusion[3][4]

动态场景

DynamicFusion

volumeDeform

BodyFusion

DoubleFusion

UnstructuredFusion

RobustFusion

KillingFusion

SurfelWarp

Fusion4D

深度学习方法[5]

  • 3-D重建基本上可以分成两种路径：一是多视角重建，二是运动重建

多视角重建

  • 多视角立体视觉(MVS，multiple view stereo)，传统MVS的方法可以分成两种：区域增长（region growing）和深度融合（depth-fusion）。

运动重建

  • 运动恢复结构（SFM）是基于背景不动的前提，机器人的研究者称之为SLAM。
  • 在机器人领域成为同步定位和制图（SLAM）技术，有滤波法和关键帧法两种
  • 后者精度高，在稀疏特征点的基础上可以采用集束调整（BA，Bundle Adjustment）
    • PTAM
    • ORB-SLAM1/2
    • LSD-SLAM
    • KinectFusion（RGB-D数据）
    • LOAM/Velodyne SLAM（激光雷达数据）
  • 视觉里程计（VO）是SLAM的一部分，估计自身运动和姿态变化。
  • 深度学习的迅猛发展，在SLAM/SFM/VO/MVS的应用探索也就成了必然。

DeepVO

  • 基于深度递归卷积神经网络（RCNN）提出了一种端到端单目视觉里程计（VO）框架。

UnDeepVO

  • 深度神经网络估计单目相机的6-DoF姿势及其视野的深度。

VINet

  • 使用视觉和惯性传感器进行运动估计的流形（on-manifold）序列到序列的学习方法。消除相机和IMU之间繁琐的手动同步，无需手动校准；模型自然地结合特定领域信息，显著地减轻漂移。

SfM-Net

  • 用于视频运动估计几何觉察的神经网络，根据场景、目标深度、相机运动、3D目标旋转和平移等来分解帧像素运动。

CNN-SLAM

  • 用于精确和密集的单目图像重建。

PoseNet

  • Kendall A, Grimes M, Cipolla R. “Posenet: A convolutional network for real-time 6-dof camera relocalization”，IEEE ICCV. 2015
  • 实时单目6 DOF重定位系统。

VidLoc

  • 用于视频片段6-DoF定位的递归卷积模型。

NetVLAD

  • 基于视觉的位置识别问题要求快速准确地识别给定查询照片的位置。

Learned Stereo Machine

  • 用于多视角立体视觉的深度学习系统，即学习立体视觉机（LSM）。

DeepMVS

  • 用于多视角立体视觉（MVS）重建的深度卷积神经网络（ConvNet）。

MVSNet

  • 出了一种端到端深度神经网络来推断参考深度图D

Recurrent MVSNet

  • 基于递归神经网络的可扩展多视角立体视觉框架

  1. 连接 ↩︎

  2. 连接 ↩︎

  3. 连接 ↩︎

  4. 连接 ↩︎

  5. 连接 ↩︎

robotic