void land space 主页文章标签分类相册
AlexNet
| DL

AlexNet

  • AlexNet，2012Alex和Hinton在LeNet基础上进行了更宽更深的网络设计。

  • 在ILSVRC2012图像分类竞赛第一名，标志着深度学习革命的开始。

  • 亮点：

    • 首次使用GPU进行网络加速训练
    • 使用了ReLU激活函数，而非传统Sigmoid以及Tanh
    • 使用了LRN局部响应归一化
    • 在全连接层的两层中使用了Dropout随机失活神经元，减少过拟合

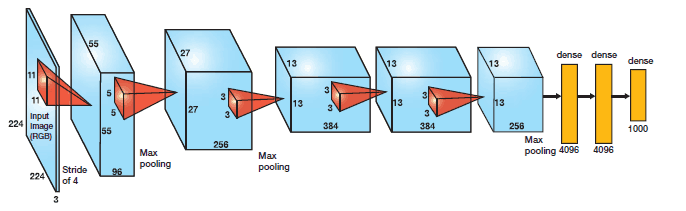
AlexNet

网络架构

AlexNet

  • AlextNet网络采用卷积神经网络架构： 5个卷积层和3个全连接层，输出层为Softmax层（识别1000类别）
id 层 输入 结构 输出 参数个数 算力
1 conv1 输入图像224*224*3 filter:96个11*11 ，stride=4，(224-11)/4+1=54.2，所以pad=3 55*55*96 (11*11*3+1)*96=35K 55*55*96*(11*11*3+1)=105M
2 pool1 55*55*96 maxpool:3*3，stride=2，(55-3)/2+1=27 27*27*96 0 0
3 conv2 27*27*96 256个5*5kernals，pad=2,(27-5+2*2)/1+1=27 27*27*256 (5*5*96+1)*256=307k 233M
4 pool2 27*27*256 maxpool:3*3，stride=2，(27-3)/2+1=13 13*13*256 0 0
5 conv3 13*13*256 filter:384个3*3,pad=1，(13-3+1*2)/1+1=13 13*13*384 (3*3*256+1)*384=884k 149M
6 conv4 13*13*384 filter:384个3*3，pad=1，(13-3+1*2)/1+1=13 13*13*384 (3*3*384+1)*384=1.3M 112M
7 conv5 13*13*384 filter:256个3*3，pad=1，(13-3+1*2)/1+1=13 13*13*256 (3*3*384+1)*256=442K 74M
8 pool5 13*13*256 maxpool:3*3，stride=2，(13-3)/2+1=6 6*6*256 0 0
9 fullconnect1 6*6*256=9216 layer:4096 4096 (9216+1)*4096=37M 37M
10 fullconnect2 4096 layer:4096 4096 (4096+1)*4096=16M 16M
11 fullconnect3 4096 layer:1000 1000 (4096+1)*1000=4M 4M
12 softmax 1000
  • N=w−F+2PS+1N=\frac{w-F+2P}{S}+1

网络改进

  • 首次引入了ReLU作为CNN 的激活函数，并验证其效果在较深的网络超过了Sigmoid，解决了Sigmoid在网络较深时的梯度弥散问题，提高了网络的训练速率。
  • 首次引入了Dropout随机忽略部分神经元，避免过拟合。随机系数0.5，也就是随机忽略一半的神经元。只在前两个全连接层使用。
  • 利用数据增强减低过拟合。利用随机裁剪和翻转镜像操作增加训练数据量。
    1. 图像平移与水平反射（镜像）:测试时，网络剪裁5个224×224图块（4个角图块和1个中心图块）以及它们的水平反射（总共10个）进行预测，并对网络的softmax层的预测求10个图块平均值。如果没有该方案， AlexNet网络会遭受严重的过拟合，这将迫使使用更小的网络
    2. 改变训练集RGB通道的图像像素强度(intensity)：对每一RGB像素Ix,y=[IxyR,IxyG,IxyB]I_{x,y}=[I_{xy}^R,I_{xy}^G,I_{xy}^B]，加上[p1,p2,p3][α1λ1,α2λ2,α3λ3]T[p_1,p_2,p_3][\alpha_1\lambda_1,\alpha_2\lambda_2,\alpha_3\lambda_3]^T，其中pi,λ是像素RGB的3*3协方差矩阵的特征向量和特征值。α均值为0，标准差0.1的随机变量。该方法即增加了目标对光照强度和颜色变化的鲁棒性，把top-1错误率减少了1%.
  • 使用重叠最大池化(Overlapping max pooling)。最大池化可以避免平均池化的模糊化效果，而采用重叠技巧可提升特征的丰富性。每次移动的步幅小于池化的边长。
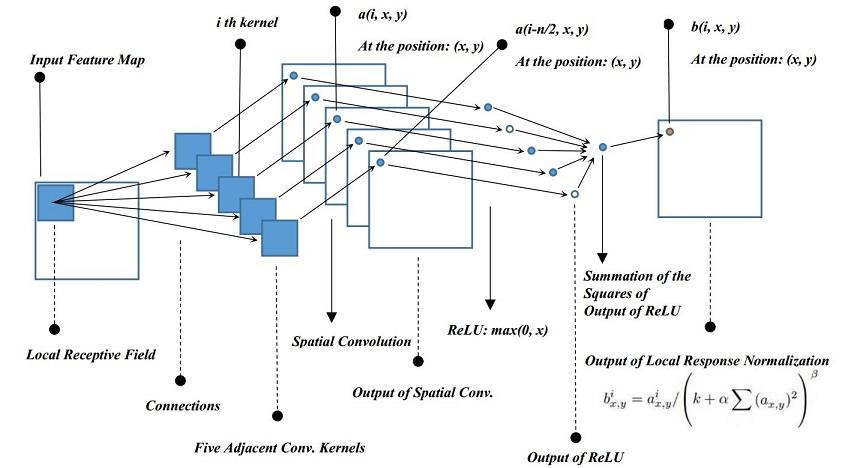
  • 提出了局部响应归一化(Local Response Normalization,LRN) 层，对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。
  • 双GPU并行计算，在第三个卷积层Conv3和全连接层做信息交互。利用GPU的并行计算能力加速网络训练过程，并采用GPU分块训练的方式解决显存对网络规模的限制

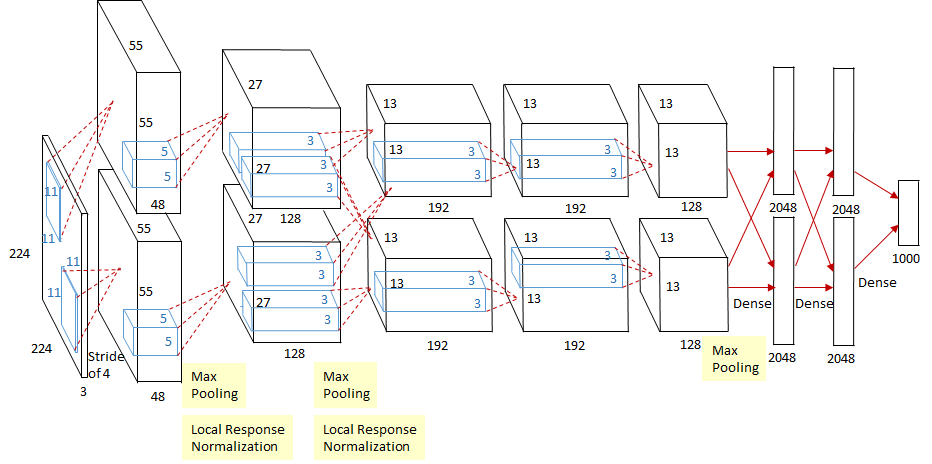
双GPU并行计算

LRN

  • 模拟在神经生物学中有一个概念叫做“ 侧抑制(Lateral inhibition)”。其含义是被激活的神经元会对相邻的神经元产生抑制作用。对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。

LRN

  • 算法功能是在池化之后，对通道间的数据进行了距离相关函数的归一化。

  • bx,yi=aix,y(k+α∑min(N−1,i+n/2)j=max(0,i−n/2)(ax,yj)2)βb_{x,y}^{i}=\frac{a_{i}^{x,y}}{(k+\alpha\sum_{min(N-1,i+n/2)}^{j=max(0,i-n/2)}{(a_{x,y}^{j})^2})^\beta}

    • ax,yja_{x,y}^{j}:第i个卷积核在位置(𝑥, 𝑦)运用ReLU后的特征图上的输出
    • bx,yib_{x,y}^{i}: LRN的输出，也是下一层的输入
    • nn:同一位置上邻近深度卷积核的数目（沿通道方向); 自己决定; AlexNet选择5
    • NN:卷积核的总数目
    • k,α,βk,\alpha,\beta:都是超参。 AlexNet选择 k = 2, α = 10e-4, β = 0.75

  • 改变超参数可以实现其它归一化操作，如当k = 0, n=N, α = 1, β = 0.5便是经典的𝑙2归一化

  • 2015年VGGNet论文Very Deep Convolutional Networks for Large-Scale Image Recognition提到LRN对VGGNet作用不大

损失函数

  • Softmax回归：是逻辑回归对处理多个类别的情况的推广。优化目标，相当于在预测分布下最大化训练样本中正确标签的对数概率的平均值

J(θ)=−1m[∑i=1m∑j=1kl(y(i)=j)log⁡eθjTx(i)∑1≤l≤kθjTx(i)]J(\theta)=-\frac{1}{m}\left [\sum_{i=1}^{m}\sum_{j=1}^{k}l(y^{(i)}=j)\log{\frac{e^{\theta^{T}_{j}x^{(i)}}}{\sum_{1\le l\le k}{\theta^{T}_{j}x^{(i)}}}} \right ]

  • 采用独热One-hot标签编码时，目标误差函数等同于交叉熵损失

网络训练

  • 改进随机梯度下降

vi+1=0.9vi−0.0005ϵωi−ϵ⟨∂L∂ω∣wi⟩v_{i+1}=0.9v_i-0.0005\epsilon \omega_i-\epsilon\left \langle \frac{\partial L}{\partial \omega}|_{w_i} \right \rangle

ωi+1=ωi+vi+1\omega_{i+1}=\omega_i+v_{i+1}

  • 动量=权重衰减-学习率*梯度下降
  • 学习率随梯度变化变缓而减小

代码

import torch.nn as nn
import torch
class AlexNet(nn.Module):
    def __init__(self, num_classes=1000, init_weights=False):
        super(AlexNet, self).__init__()
        self.features = nn.Sequential(
            nn.Conv2d(3, 48, kernel_size=11, stride=4, padding=2),  # input[3, 224, 224]  output[48, 55, 55]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[48, 27, 27]
            nn.Conv2d(48, 128, kernel_size=5, padding=2),           # output[128, 27, 27]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[128, 13, 13]
            nn.Conv2d(128, 192, kernel_size=3, padding=1),          # output[192, 13, 13]
            nn.ReLU(inplace=True),
            nn.Conv2d(192, 192, kernel_size=3, padding=1),          # output[192, 13, 13]
            nn.ReLU(inplace=True),
            nn.Conv2d(192, 128, kernel_size=3, padding=1),          # output[128, 13, 13]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[128, 6, 6]
        )
        self.classifier = nn.Sequential(
            nn.Dropout(p=0.5),
            nn.Linear(128 * 6 * 6, 2048),
            nn.ReLU(inplace=True),
            nn.Dropout(p=0.5),
            nn.Linear(2048, 2048),
            nn.ReLU(inplace=True),
            nn.Linear(2048, num_classes),
        )
        if init_weights:
            self._initialize_weights()
    def forward(self, x):
        x = self.features(x)
        x = torch.flatten(x, start_dim=1)
        x = self.classifier(x)
        return x
    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
                if m.bias is not None:
                    nn.init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                nn.init.normal_(m.weight, 0, 0.01)
                nn.init.constant_(m.bias, 0)
algorithm