简介^[1]

• 判断两个给定线段是否相交，考虑向量叉乘。

叉乘

• 向量a(x1,y1)，向量b(x2,y2)

• 叉乘：$a\times b=\begin{bmatrix}x_1,y_1\\x_2,y_2\end{bmatrix}=x_1\dot{y_2}-x2\dot{y1}=|a|\dot|b|\sin\theta$

• 根据$\sin\theta$我们可知：

  • $a\times b<0$，表示向量b在向量a的顺时针方向；
  • $a\times b>0$，表示向量b在向量a的逆时针方向；
  • $a\times b=0$，表示向量a与向量b平行。

• 顺逆时针是指两向量平移至起点相连，从某个方向旋转到另一个向量小于180度。如下图：

判断相交

• 假设有两条线段AB，CD，若AB，CD相交，我们可以确定：
  1. 线段AB与CD所在的直线相交，即点A和点B分别在直线CD的两边；
  2. 线段CD与AB所在的直线相交，即点C和点D分别在直线AB的两边；
• 上面两个条件同时满足是两线段相交的充要条件，所以我们只需要证明点A和点B分别在直线CD的两边，点C和点D分别在直线AB的两边，这样便可以证明线段AB与CD相交了。

使用叉乘定理判断

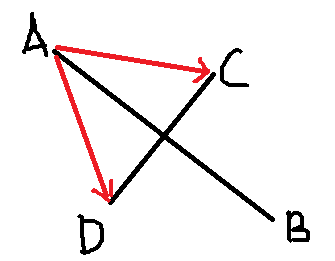
• 在上图中，线段AB与线段CD相交，于是我们可以得到两个向量AC，AD，C和D分别在AB的两边，向量AC在向量AB的逆势针方向，AB×AC > 0；向量AD在向量AB的顺势针方向，AB×AD < 0，两叉乘结果异号。

• 这样，方法就出来了：如果线段CD的两个端点C和D，与另一条线段的一个端点（A或B，只能是其中一个）连成的向量，与向量AB做叉乘，若结果异号，表示C和D分别在直线AB的两边，若结果同号，则表示CD两点都在AB的一边，则肯定不相交。

• 当然，不能只证明C，D在直线AB的两边，还要用相同的方法证明A，B在直线CD的两边，两者同时满足才是线段相交的充要条件。

几种特殊情况

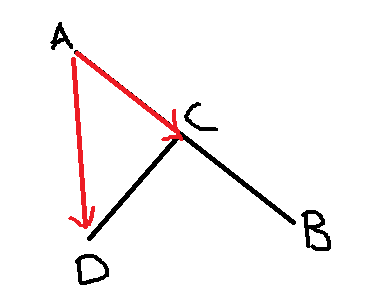
1. 只有1点相交，线段AB与CD相交于C点，按照之前介绍的方法，我们可以连成两向量AD和AC，这时候，我们发现，AC与AB共线，AB×AC = 0；而AB×AD < 0；两者并不异号，可实际上仍然相交。所以当出现两叉乘结果中，有一方为0，也可以看成点CD在直线AB的两边。

2. 两条线段重合，线段AB与线段CD重合，重合部分为CB，这种重合的情况要特殊判断：

• 首先，我们给没条线段的两个端点排序，大小判断方法如下：横坐标大的点更大，横坐标相同，纵坐标大的点更大。
• 排好序后，每条线段中，小的点当起点，大的当终点。我们计算向量AB×向量CD，若结果为0，表示线段AB平行CD，平行才有了重合的可能；但平行也分共线和不共线，只有共线才有可能重合

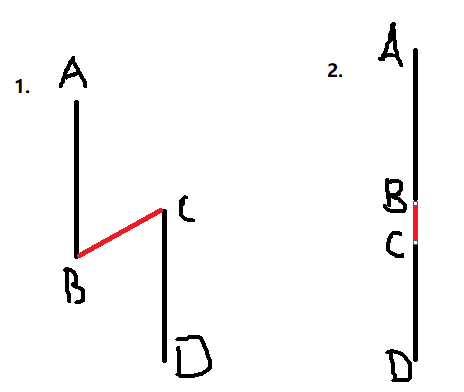
• 判断共线我们可以在两条线段中各取一点，用这两点组成的向量与其中一条线段进行叉乘，结果若为0，就表示两线段共线。我们取向量BC，若BC×CD = 0，表示两点共线，即是第二种情况，否则就是第一种情况。

• 然而，即使他们共线，却还是不一定重合，就如上图中第二种情况。这时候，之前给点排序的妙处就体现出来了：

• 若一条线段AB与另一条线段CD共线，且线段AB的起点小于等于线段CD的起点，但线段AB的终点（注意是终点）大于等于线段CD的起点（注意是起点），或者交换一下顺序，CD的起点小于AB的起点…只要满足其中一个，就表示有重合部分。

---

1. 连接 ↩︎